Ряды с произвольными членами. Абсолютная и условная сходимости. Признак абсолютной сходимости. Признаки Лейбница, Абеля, Дирихле
1. Ряды с произвольными членами. Абсолютная и условная сходимости
Пусть
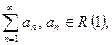
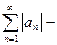 ряд с положительными членами (2)
ряд с положительными членами (2)
Ряд (1) называется абсолютно сходящимся, если сходится ряд (2). Сходящийся ряд (1) называют условно сходящимся, если он абсолютно расходится.
2. Признак абсолютной сходимости
Абсолютно сходящийся ряд является сходящимся.
Доказательство.Основано на применении критерия Коши.
Ряд (2) – сходится Þ (по критерию Коши) Þ 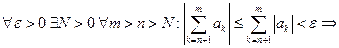
Þ (по критерию Коши) Þ ряд (1) – сходится. Доказано.
3. Признак Лейбница
Существуют ли условно сходящиеся ряды?
Рассмотрим класс знакочередующихся рядов: 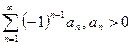 (3).
(3).
Признак Лейбница.
Если для ряда (3) выполнены условия:
1) 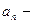 невозрастающая;
невозрастающая;
2) 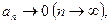
то ряд (3) сходится и справедлива оценка остатка 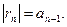
Доказательство.Рассмотрим 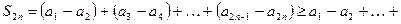
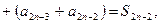 т.е.
т.е. 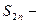 неубывающая. С другой стороны
неубывающая. С другой стороны 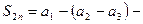
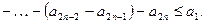 Итак, последовательность
Итак, последовательность 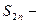 неубывающая и ограниченная сверху и
неубывающая и ограниченная сверху и 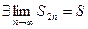 . Для последовательности частичных сумм с нечётными номерами
. Для последовательности частичных сумм с нечётными номерами 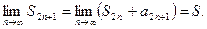 Значит,
Значит, 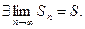
Остаётся оценить остаток: 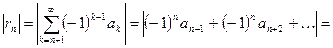
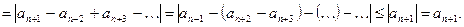
Доказано.
Пример. 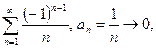
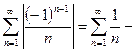 расходится
расходится
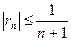
Исходный ряд сходится условно.
4. Признаки Абеля, Дирихле
Пусть дан ряд 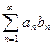 (1).
(1).
Введём преобразования Абеля
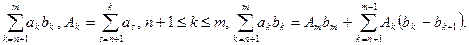
Доказательство. 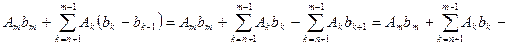
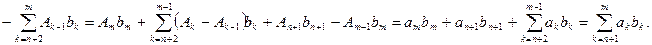
Доказано.
С помощью преобразования Абеля доказываются следующие признаки сходимости ряда (1).
Признак Дирихле.
Если
1) 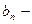 невозрастающая и стремится к нулю
невозрастающая и стремится к нулю 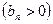 ;
;
2) 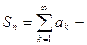 ограниченная,
ограниченная,
то ряд (1) – сходится.
Доказательство.Воспользуемся критерием Коши и будем оценивать суммы:
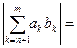 (по преобразованию Абеля)
(по преобразованию Абеля) 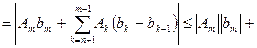
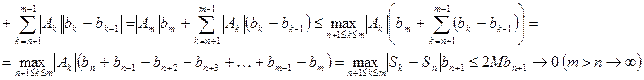 и по критерию Коши ряд (1) сходится.
и по критерию Коши ряд (1) сходится.
Доказано.
Признак Абеля.
Если
1) 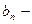 монотонная и ограниченная;
монотонная и ограниченная;
2) 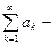 сходится,
сходится,
то ряд (1) – сходится.
Доказательствоаналогично доказательству признака Дирихле.
Частным случаем признака Дирихле является признак Абеля.
Если 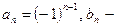 монотонно убывает и стремится к нулю, то
монотонно убывает и стремится к нулю, то 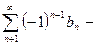 сходится (2).
сходится (2).
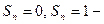 ограниченные, значит ряд (2) сходится.
ограниченные, значит ряд (2) сходится.
Рассмотрим ряд 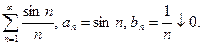
Оценим суммы 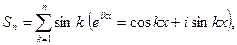
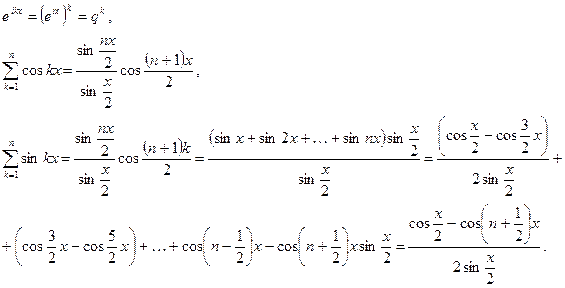
Справедливы оценки
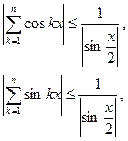
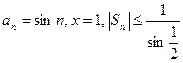 и по признаку Дирихле ряд сходится.
и по признаку Дирихле ряд сходится.
Задача. Исследовать на сходимость ряд 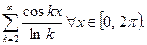
Указание. Рассмотреть 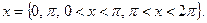
ЛЕКЦИЯ 17
Условная и безусловная сходимости. Теорема Римана о перестановках условно сходящегося ряда. Критерий безусловной сходимости. Сходимость бесконечного произведения. Необходимое условие сходимости. Сведение сходимости бесконечного произведения к сходимости числового ряда. Абсолютная и условная сходимости
1. Условная и безусловная сходимости. Теорема Римана о перестановках условно сходящегося ряда
Биекция 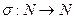 называется числовой перестановкой N.
называется числовой перестановкой N.
Если 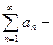 числовой ряд (1), то ряд вида
числовой ряд (1), то ряд вида 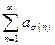 называется его перестановкой.
называется его перестановкой.
Пример. 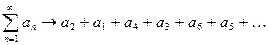 называется его перестановкой.
называется его перестановкой.
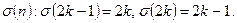
Если ряд (1) сходится для любой перестановки и к той же сумме, то он называется безусловно сходящимся.
Теорема Римана.Если ряд (1) сходится условно, то 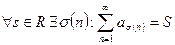 и существуют перестановки, для которых переставленный ряд расходится.
и существуют перестановки, для которых переставленный ряд расходится.
Введем некоторые обозначения:
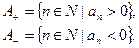
Доказательство.Пусть ряд (1) – сходится условно, 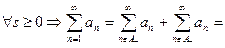
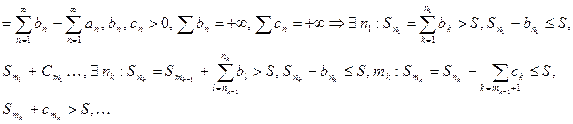
В итоге построен ряд 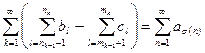 . Получили ряд, являющийся перестановкой исходного ряда.
. Получили ряд, являющийся перестановкой исходного ряда.
Нужно показать, что эта перестановка сходится к числу S. Возможны четыре случая, пусть 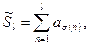 тогда
тогда
1) 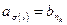 ;
;
2) 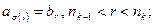
3) 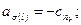
4) 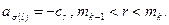
Оценим разность 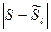 в каждом из четырёх случаев.
в каждом из четырёх случаев.
1) 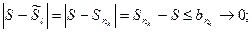
2) 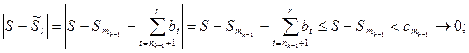
3) 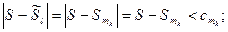
4) 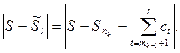
Доказано.
Ряд (1) называется универсальным относительно перестановок, если 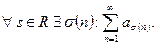
Теорема (об универсальных рядах).Ряд (1) – универсальный относительно перестановок Û
1) 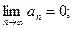
2) 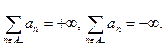
Следствие: условно сходящийся ряд является универсальным относительно перестановок.
Задача. Проверить выполнение условий (1), (2) теоремы об универсальных рядах для условно сходящегося ряда.
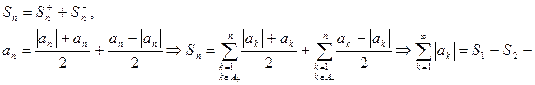
противоречие.
Можно определить и другие понятия универсального числового ряда, например, универсальный относительно знака: ряд (1) – универсальный относительно знака, если 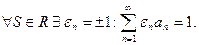
Задача. Пусть ряд 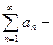 сходится. Что можно сказать о сходимости рядов
сходится. Что можно сказать о сходимости рядов 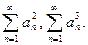
Ряд 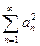 не обязан сходиться, например
не обязан сходиться, например 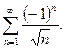
Ряд 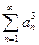 также не обязан сходиться. Построить пример.
также не обязан сходиться. Построить пример.
2. Критерий безусловной сходимости
Теорема (о безусловной сходимости).Ряд (1) – сходится безусловно тогда и только тогда, когда ряд (1) сходится абсолютно.
Доказательство.Необходимость.
(1) – сходится безусловно Þ (от противного) Þ (1) – сходится условно (по теореме Римана) Þ (1) – не сходится безусловно – противоречие Þ (1) – сходится абсолютно.
Достаточность.
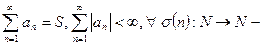 перестановка
перестановка 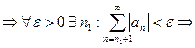
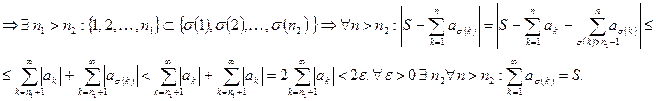 Доказано.
Доказано.
Замечание. Для абсолютно сходящегося ряда модуль суммы будет:
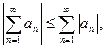 т.к.
т.к. 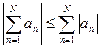 при
при 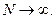
3. Сходимость бесконечного произведения. Необходимое условие сходимости
Пусть 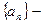 положительная последовательность, т.е.
положительная последовательность, т.е. 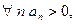 .
.
Формальная запись (1) 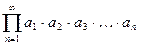 называется бесконечным произведением.
называется бесконечным произведением.
Будем говорить, что бесконечное произведение (1) – сходится, если 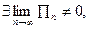 где
где 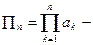 последовательность частичных произведений. В противном случае произведение (1) – расходится.
последовательность частичных произведений. В противном случае произведение (1) – расходится.
Необходимое условие сходимости. Если (1) сходится, то 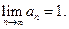
Действительно, 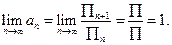
4. Сведение сходимости бесконечного произведения к сходимости числового ряда. Абсолютная и условная сходимости
Основная теорема.Бесконечное произведение (1) – сходится 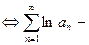 сходится (2).
сходится (2).
Доказательство.(1) – сходится 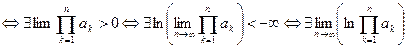
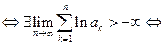 (2) – сходится.
(2) – сходится.
Доказано.
Пример. Исследовать сходимость ряда 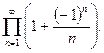
Получаем 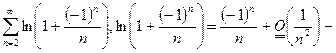 сходится условно.
сходится условно.
Исходный ряд сходится условно.
Бесконечное произведение (1) назовём абсолютно сходящимся, если сходится ряд 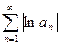 . В противном случае (1) сходится условно. В предыдущем примере представлено условно сходящееся бесконечное произведение.
. В противном случае (1) сходится условно. В предыдущем примере представлено условно сходящееся бесконечное произведение.
Для дальнейшего удобно обозначить 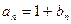 и рассматривать
и рассматривать 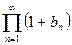 (3),
(3), 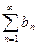 (4),
(4), 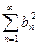 (5).
(5).
Теорема.Произведение (3) – сходится абсолютно 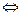 (4) сходится абсолютно.
(4) сходится абсолютно.
Доказательство.(3) сходится абсолютно 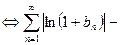 сходится и в частности
сходится и в частности 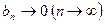 . Сравним ряды
. Сравним ряды 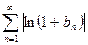 и
и 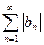 при условии
при условии 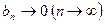 :
: 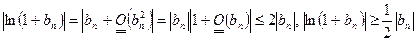 для
для 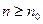 . Из этих неравенств вытекает, что эти ряды сходятся абсолютно.
. Из этих неравенств вытекает, что эти ряды сходятся абсолютно.
Доказано.
Следствие:если в произведении (3) все bn, начиная с некоторого номера, имеют один и тот же знак, то сходимость произведения (3) эквивалентна сходимости ряда (4).
Пример. 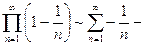 расходится.
расходится.
Анализ этой теоремы показывает, что удобно использовать разложение  .
.
Задача. Обозначим: «+» - сходится, «-» - расходится, и заполним следующую таблицу:
| (4) | (5) | (3) | |
| 1. | + | + | + |
| 2. | + | - | - |
| 3. | - | + | - |
| 4. | - | - | ? |
Доказательство 1. 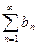 ,
, 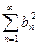 - сходятся
- сходятся 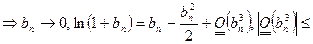
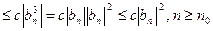 . Доказано.
. Доказано.
Пример. 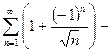 сходится, т.к.
сходится, т.к. 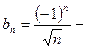 сходится, но
сходится, но 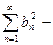 расходится.
расходится.
Доказательство 2.Опять 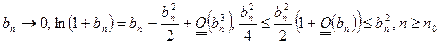 и из признака сравнения ряд
и из признака сравнения ряд 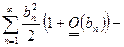 расходится. Общий член есть сумма двух последовательностей – сходящейся и расходящейся, значит, ряд
расходится. Общий член есть сумма двух последовательностей – сходящейся и расходящейся, значит, ряд 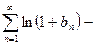 расходится, иначе ряд
расходится, иначе ряд 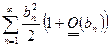 был бы сходящимся как разность двух сходящихся рядов. Доказано.
был бы сходящимся как разность двух сходящихся рядов. Доказано.
Доказательство 3.Опять 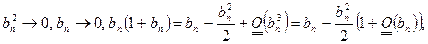
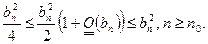 И как в предыдущем случае ряд
И как в предыдущем случае ряд 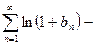 сходится.
сходится.
Доказано.
Доказательство 4.Два примера:
1) “-”, “-”Þ “-” 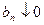 ;
;
2) “-”, “-”Þ “+”.
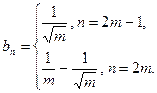
Ряд 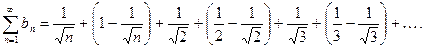 Частичная сумма порядка совпадает с частичной суммой гармонического ряда, т.е. ряд расходится.
Частичная сумма порядка совпадает с частичной суммой гармонического ряда, т.е. ряд расходится.
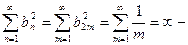 расходится. Оба ряда расходятся.
расходится. Оба ряда расходятся.
Вычислим частичное произведение 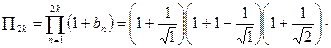
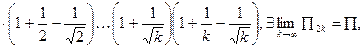 т.к. произведение
т.к. произведение 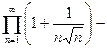 расходится по следствию:
расходится по следствию: 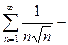 обобщённый гармонический ряд с показателем p =
обобщённый гармонический ряд с показателем p = 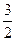 - сходится.
- сходится.
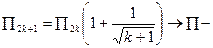 сходится к тому же числу, а значит и всё произведение сходится.
сходится к тому же числу, а значит и всё произведение сходится.
Доказано
Библиографический список
Основная литература
1. Ильин В.А., Поздняк Э.Г. Основы математического анализа. М.: Физматлит, Ч.1, 2002. – 646с., Ч. 2, 2002. – 447с.
2. Зорич В.А. Математический анализ. М.: МЦНМО, Ч.1, 2002. – 657с., Ч. 2, 2002. – 787с.
3. Кузнецов, Л. А. Сборник заданий по высшей математике. Типовые расчеты : учеб. пособие для вузов / Л. А. Кузнецов .— 10-е изд., стер. — СПб. ; М. ; Краснодар : Лань, 2008 .— 240 с.
4. Глаголев В.В., Иванов В.И., Смирнов О.И., Горбачев Д.В. Сборник заданий по математическому анализу. Типовые расчеты с примерами решений. Ч. 1. Тула: ТулГУ, 2007. – 172с.
5. Глаголев В.В., Иванов В.И., Смирнов О.И. Сборник заданий по математическому анализу. Типовые расчеты. Тула: ТулГУ, 2010. – 96с.
Дополнительная литература
1. Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Дрофа, 2004. – 640с.
2. Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. М.: Высшая школа, Кн.1, 2002. – 728с., Кн.2, 2002. – 712с.
3. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: АСТ, 2007. – 560с.
4. Золотухин А.Я. Элементы теории множеств, меры и интеграла Лебега. Тула: ТулГУ, 2007. – 107с.
5. Рудин У. Основы математического анализа. СПб.: Лань, 2004. – 320с.
Периодические издания
1. Вестник МГУ. Серия 1. Математика. Механика. — М.: МГУ.— ISSN 0579-9368.
