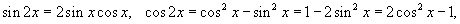Определение неопределенного интеграла.
Определение первообразной.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 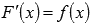 для любого х из заданного промежутка.
для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 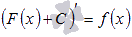 . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Проверка.
Для проверки результата продифференцируем полученное выражение:
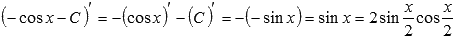
В итоге получили подынтегральную функцию, значит, интегрирование выполнено правильно. В последнем переходе была использована формула синуса двойного угла.
№2 Теорема о множестве первообразных
Теорема о множестве первообразных: Если f(x) имеет в данном промежутке первообразную F(x), то все первообразные данной функции заключены в выражении F(x) + С. Две первообразные одной функции отличаются друг от друга только на константу. Неопределенный интеграл: пусть f(x) имеет на ( a, b ) F(x), такую, что F/(x) = f(x) или dF(x) = f(x)dx, тогда F(x) + С –является общим выражением для всех первообразных и называется неопределенным интегралом от заданной функции f(x). Свойства: 1) Если f(x) непрерывна на ( a, b ), то на ( a, b ) существует F(x) и неопределенный интеграл.
№3 Внесение под знак дифференциала
При сведении заданного интеграла к табличному часто используются следующие преобразования дифференциала как операция «подведения под знак дифференциала». При этом используется формула: 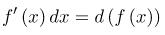
Вообще говоря, внесение (подведение) под знак дифференциала и замена переменной (метод подстановки) – это один и тот же метод нахождения неопределенного интеграла; отличие состоит только в оформлении.
Суть метода. Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то есть если 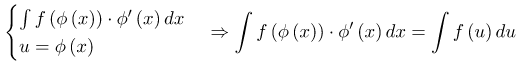
№4

№5 



№6 Интегрирование по частям.




 №7 Простейшие рациональные дроби и их интегрирование.
№7 Простейшие рациональные дроби и их интегрирование.




 №9
№9


№10


№11
1. Интегралы вида 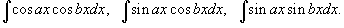 Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность: Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность: 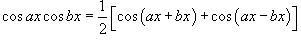 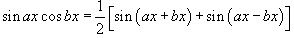 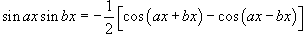 2. Интегралы вида 2. Интегралы вида 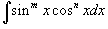 Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования: Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:
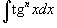 Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения 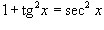 и формулы редукции и формулы редукции 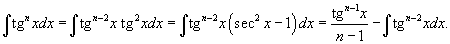 4. Интегралы вида 4. Интегралы вида 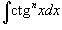 Здесь степень подынтегрального выражения понижается с помошью соотношения Здесь степень подынтегрального выражения понижается с помошью соотношения 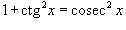 и формулы редукции и формулы редукции 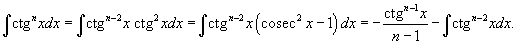 |
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы: 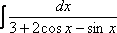 ,
, 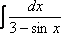 ,
, 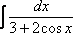 ,
, 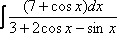 и т.д.
и т.д.
(1) Производим в исходный интеграл подстановку: 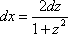 ,
, 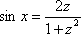 ,
, 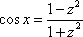 .
.
(2) Приводим знаменатель к общему знаменателю.
(3) Избавляемся от четырехэтажности дроби, при этом 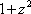 у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.
у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.
(4) Приводим подобные слагаемые в знаменателе.
(5) Интеграл 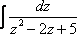 решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение
решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение 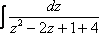 является подготовкой для осуществления вышеуказанного приёма
является подготовкой для осуществления вышеуказанного приёма
(6) Выделяем полный квадрат и готовим интеграл для интегрирования.
(7) Интегрируем по табличной формуле 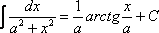 .
.
(8) Проводим обратную замену, вспоминая, что 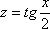 .
.
№12

№14 Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 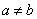 ) называется приращение какой-нибудь её первообразной на данном отрезке.
) называется приращение какой-нибудь её первообразной на данном отрезке.
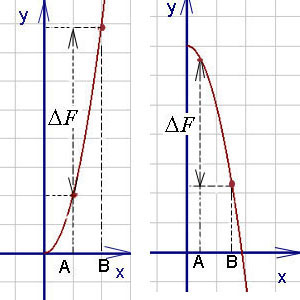
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
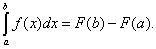 (38)
(38)
Равенство (38) называется формулой Ньютона-Лейбница.
Основные свойства:
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 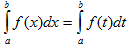 , где х, t – любые буквы.
, где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
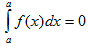
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
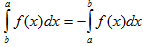
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
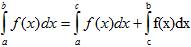
V. Постоянный множитель можно выносить за знак определенного интеграла.
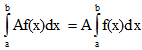
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
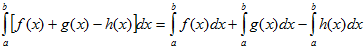
№151. Постоянный множитель можно выносить за знак определённого интеграла:
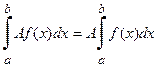 .
.
2. Если функции f(x) и g(x) интегрируемы на  , то определённый интеграл их алгебраической суммы равен алгебраической сумме интегралов от слагаемых:
, то определённый интеграл их алгебраической суммы равен алгебраической сумме интегралов от слагаемых:
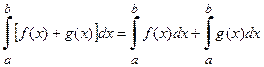 .
.
Замечание: Свойство справедливо для любого конечного числа слагаемых.
Следствие:
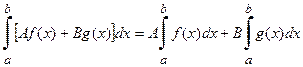
(свойство линейности операции интегрирования).
3. Если отрезок 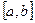 разбит точкой С на части, то интеграл по всему промежутку равен сумме интегралов по его частям (при любом расположении точек a, b, и с).
разбит точкой С на части, то интеграл по всему промежутку равен сумме интегралов по его частям (при любом расположении точек a, b, и с).
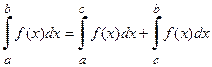
(свойство аддитивности).
№16 -17




№29-30



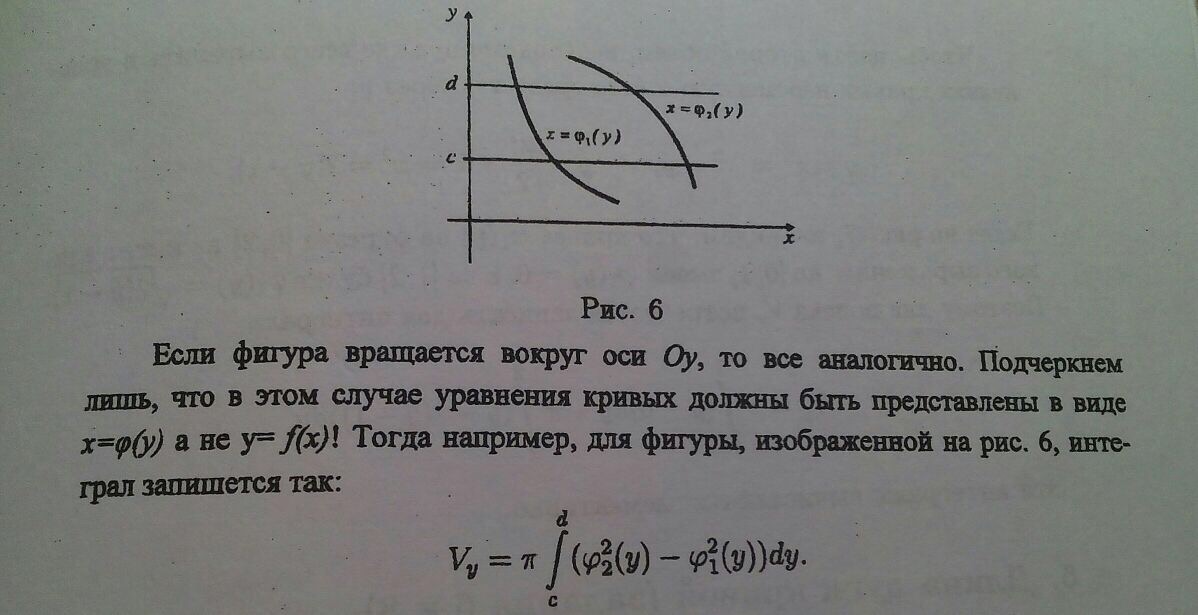
№31 



№32




№39 Производная по направлению
Производная по направлению
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Пусть в области 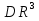 задано скалярное поле u
задано скалярное поле u 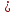 u(x;y;z) и задан трёхмерный вектор
u(x;y;z) и задан трёхмерный вектор 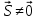 . Рассмотрим некоторую фиксированную точку P0(х0;у0;z0)
. Рассмотрим некоторую фиксированную точку P0(х0;у0;z0) 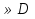 и точку P (x;y;z)
и точку P (x;y;z) 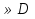 с текущими координатами, но такую, чтобы
с текущими координатами, но такую, чтобы 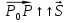 . Обозначим
. Обозначим 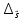 u u(P) – u(P0) – приращение функции u в точке P0 по направлению вектора
u u(P) – u(P0) – приращение функции u в точке P0 по направлению вектора 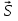 .
.
Определение 1
Производной функции u 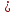 u(x;y;z) в точке P0(х0;у0;z0) по направлению
u(x;y;z) в точке P0(х0;у0;z0) по направлению
вектора 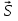 называется предел отношения приращения
называется предел отношения приращения 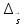 u u(P) – u(P0) к расстоянию |
u u(P) – u(P0) к расстоянию | 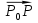 | при условиях, что P→P0(
| при условиях, что P→P0( 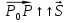 ) и этот предел существует. Обозначение:
) и этот предел существует. Обозначение:
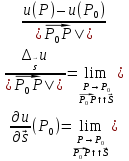
Теорема
Пусть функция u 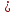 u(x;y;z) дифференцируема в точке P0(х0;у0;z0). Тогда в точке P0 существует производная функции u по направлению вектора
u(x;y;z) дифференцируема в точке P0(х0;у0;z0). Тогда в точке P0 существует производная функции u по направлению вектора 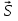 и справедливо равенство:
и справедливо равенство:
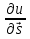 (P0)
(P0) 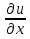 (P0)
(P0) 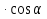 +
+ 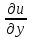 (P0)
(P0) 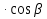 +
+ 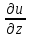 (P0)
(P0) 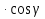 ,
,
где 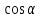 ,
, 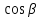 ,
, 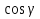 – направляющие косинусы вектора
– направляющие косинусы вектора 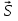 .
.
Доказательство: Возьмём точку P (x0 + 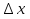 ; y0 +
; y0 + 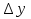 ; z0 +
; z0 + 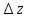 ) так, чтобы
) так, чтобы 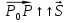 .
.
Так как функция u(x;y;z) дифференцируема в точке P0, то:
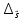 u u(P) – u(P0)
u u(P) – u(P0) 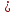
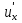 (P0)
(P0) 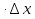 +
+ 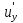 (P0)
(P0) 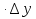 +
+ 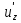 (P0)
(P0) 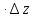 +
+ 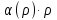 ,
,
где
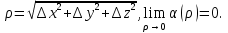
Так как 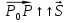 , то углы
, то углы 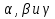 , которые составляет вектор
, которые составляет вектор 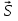 с осями координат Ох, Оу и Оz соответственно, такие же для вектора
с осями координат Ох, Оу и Оz соответственно, такие же для вектора 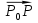 .
.
Поэтому: 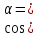
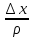 ,
, 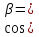
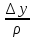 ,
, 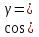
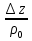
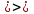
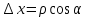 ,
, 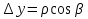 ,
, 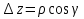 .
.
Тогда 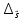 u
u 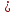
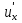 (P0)
(P0) 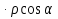 +
+ 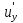 (P0)
(P0) 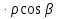 +
+ 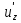 (P0)
(P0) 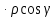 +
+ 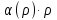 .
.
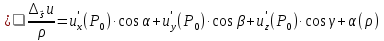
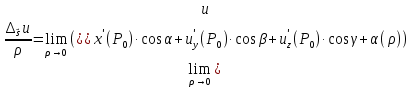
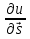 (P0)
(P0) 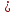
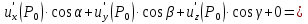
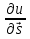 (P0)
(P0) 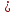
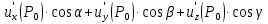 .
.
Что и требовалось доказать.
Рассмотрим частные случаи производной по координатным направлениям.
Пусть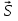 =
= 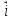 , тогда
, тогда 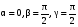
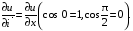
Пусть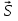 =
= 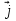 , тогда
, тогда 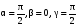
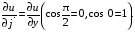
Пусть =
=  , тогда
, тогда 
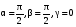
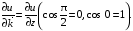
№40 Градиент. Связь градиента и производной по направлению.
Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины φ {\displaystyle \varphi } , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
С математической точки зрения на градиент можно смотреть как на:
1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента
2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных
3. Строки Матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).
Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке
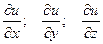 ,
,
то этот вектор называется градиентомфункции u.
Связь градиента и производной по направлению
 |  |  |
Теорема: Пусть задана функция U = U(X, Y, Z) и поле градиентов 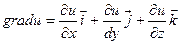 . Тогда производная . Тогда производная 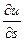 по направлению некоторого вектора по направлению некоторого вектора 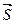 равняется проекции вектора Gradu на вектор равняется проекции вектора Gradu на вектор 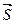 . Доказательство: Рассмотрим единичный вектор . Доказательство: Рассмотрим единичный вектор 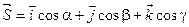 и некоторую функцию u = u(x, y, z) и найдем скалярное произведение векторов и некоторую функцию u = u(x, y, z) и найдем скалярное произведение векторов 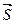 и Gradu. и Gradu. 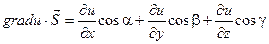 Выражение, стоящее в правой части этого равенства является производной функции u по направлению s. Т. е. Выражение, стоящее в правой части этого равенства является производной функции u по направлению s. Т. е. 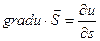 . Если угол между векторами Gradu и . Если угол между векторами Gradu и  обозначить через j, то скалярное произведение можно записать в виде произведения модулей этих векторов на косинус угла между ними. С учетом того, что вектор обозначить через j, то скалярное произведение можно записать в виде произведения модулей этих векторов на косинус угла между ними. С учетом того, что вектор  единичный, т. е. его модуль равен единице, можно записать: единичный, т. е. его модуль равен единице, можно записать: 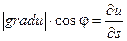 Выражение, стоящее в правой части этого равенства и является проекцией вектора Gradu на вектор Выражение, стоящее в правой части этого равенства и является проекцией вектора Gradu на вектор 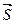 . Теорема доказана. Для иллюстрации геометрического и физического смысла градиента скажем, что градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля u в какой - либо точке. В физике существуют такие понятия как градиент температуры, градиент давления и т. п. Т. е. направление градиента есть направление наиболее быстрого роста функции. С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции . Теорема доказана. Для иллюстрации геометрического и физического смысла градиента скажем, что градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля u в какой - либо точке. В физике существуют такие понятия как градиент температуры, градиент давления и т. п. Т. е. направление градиента есть направление наиболее быстрого роста функции. С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции |
№41. Экстремум функции двух переменных. Необходимые условия экстремума. Достаточные условия экстремума. 

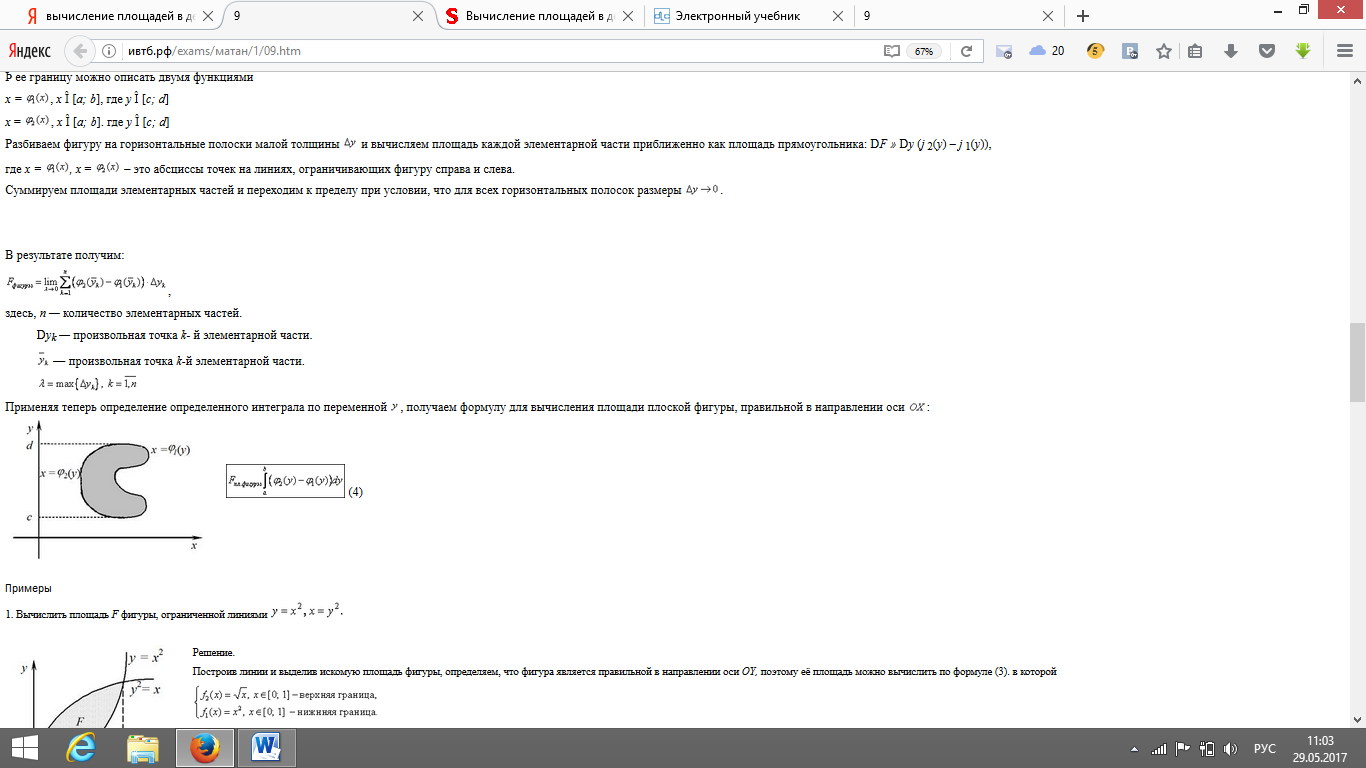
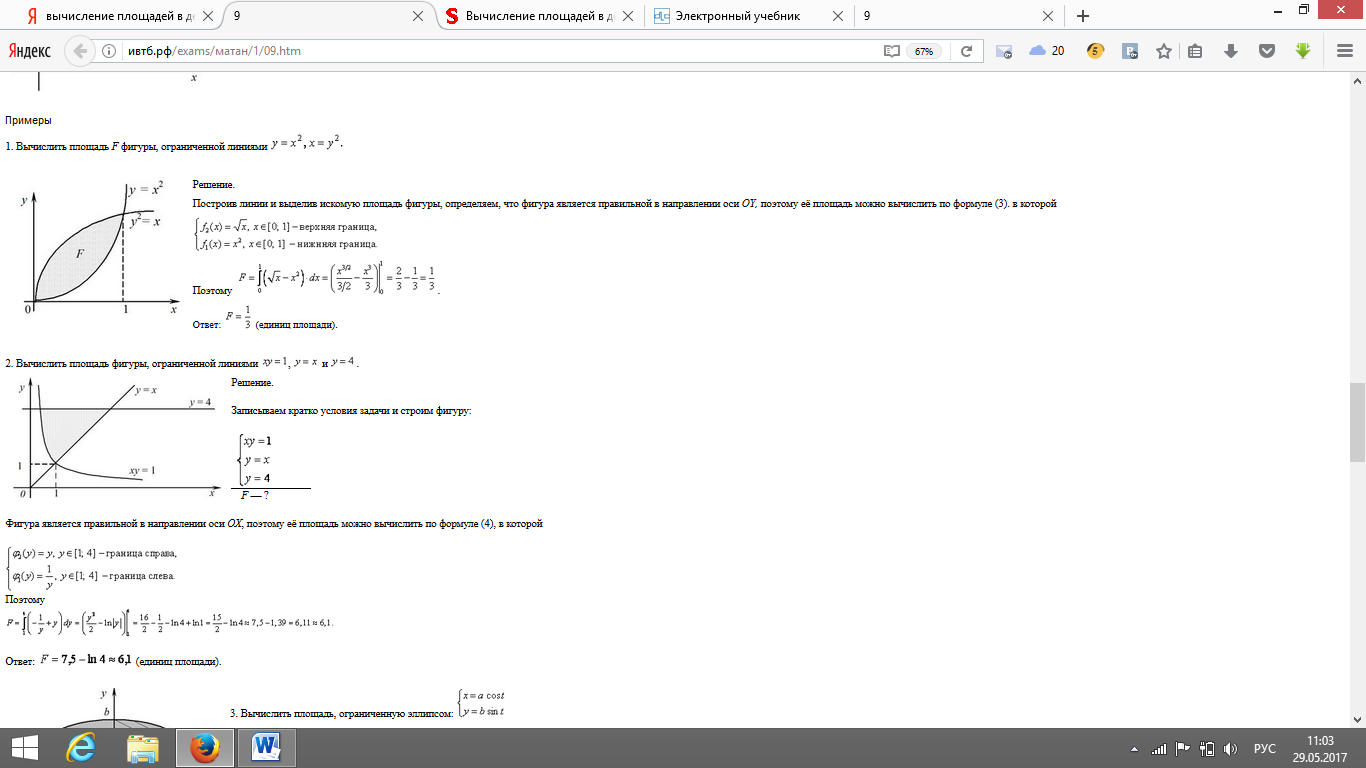
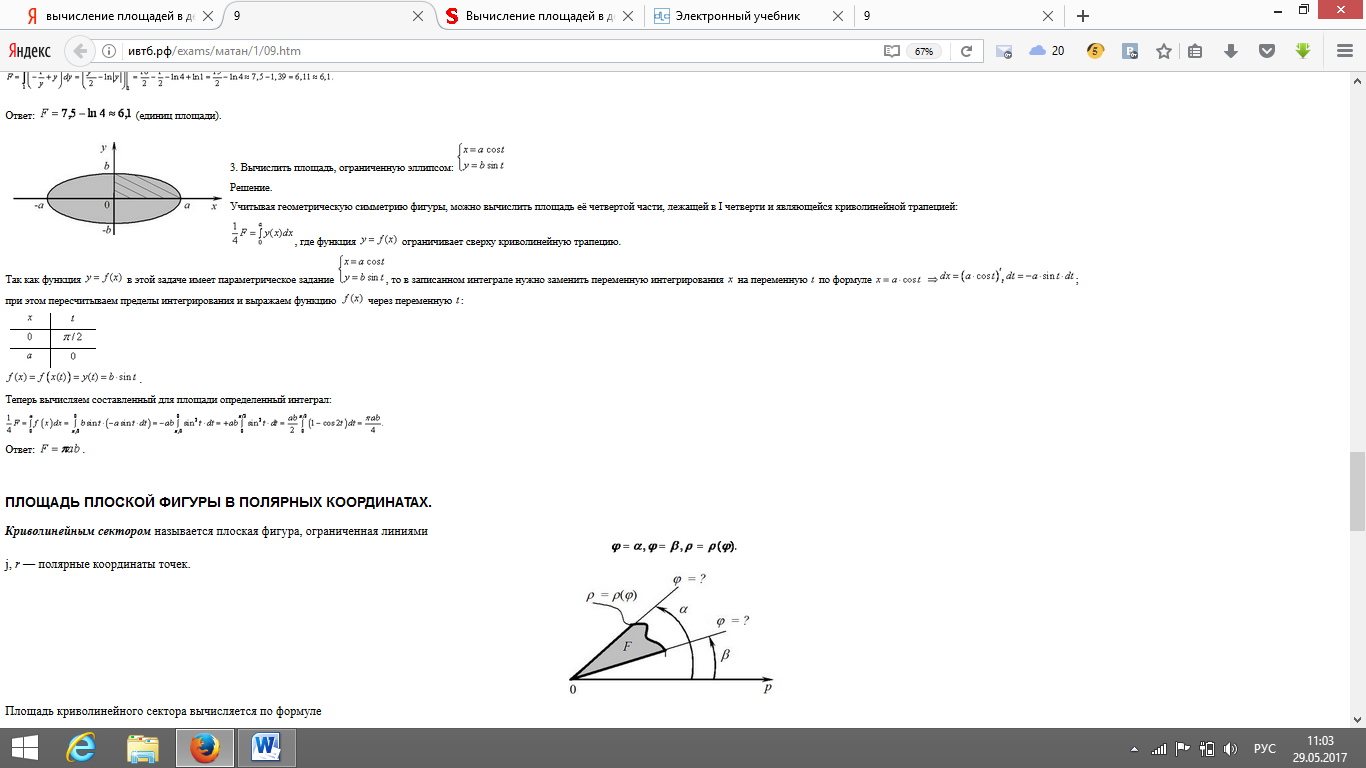
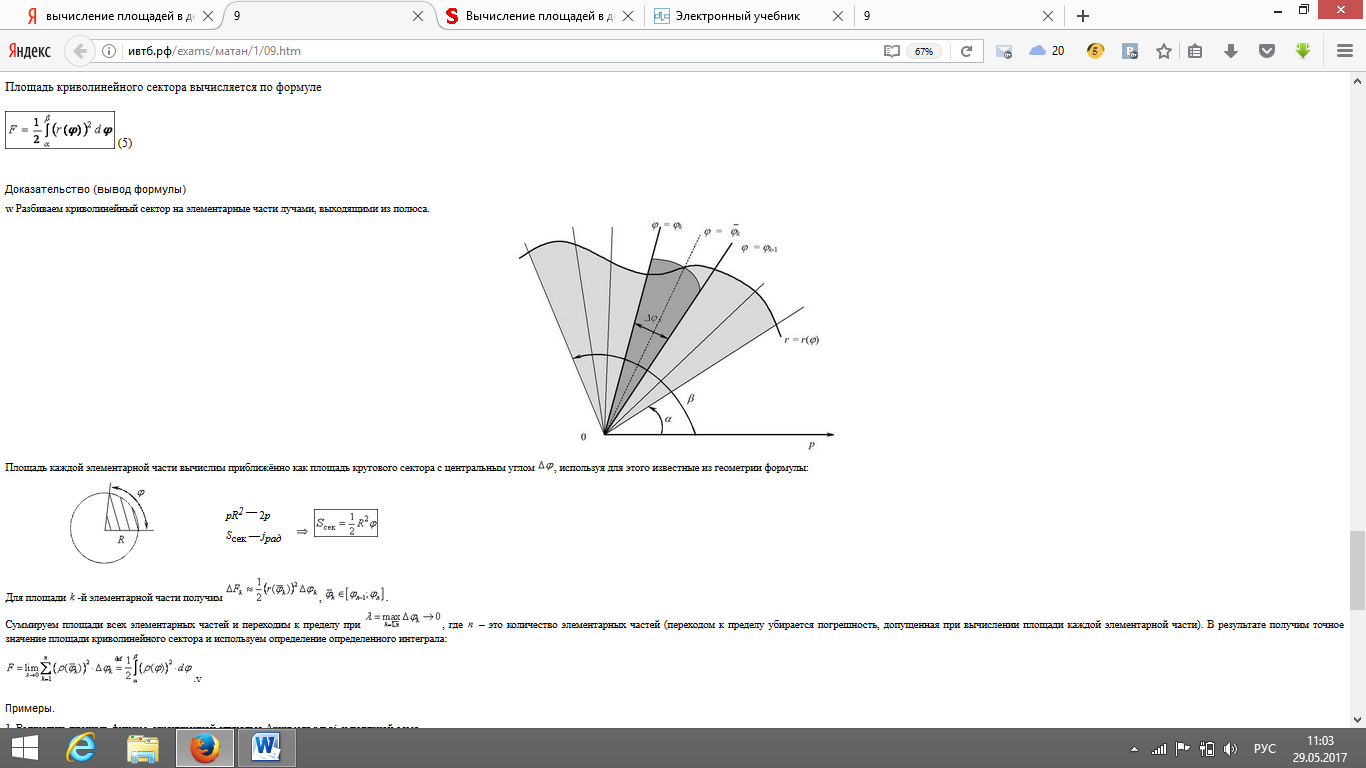
 №42 Кратные интегралы. Двойной интеграл. Его геометрический смысл.
№42 Кратные интегралы. Двойной интеграл. Его геометрический смысл. 


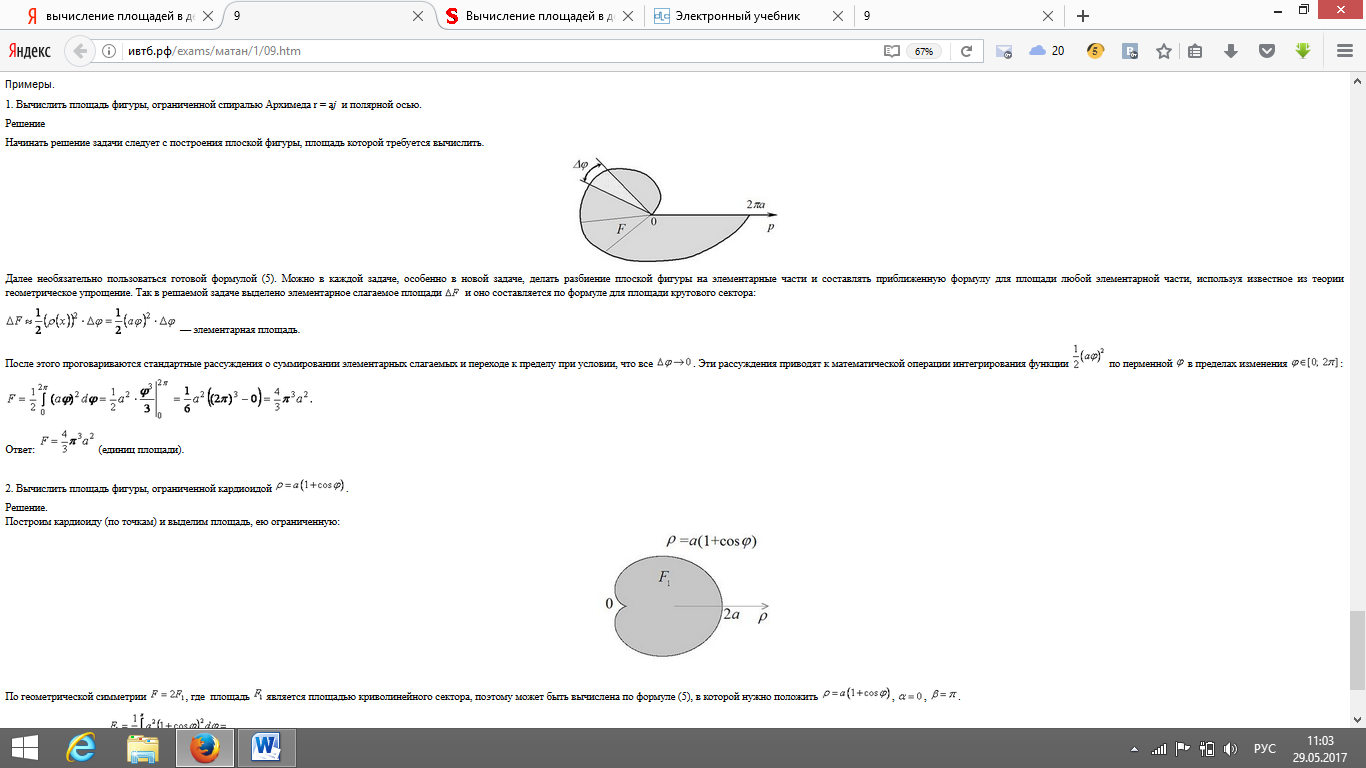
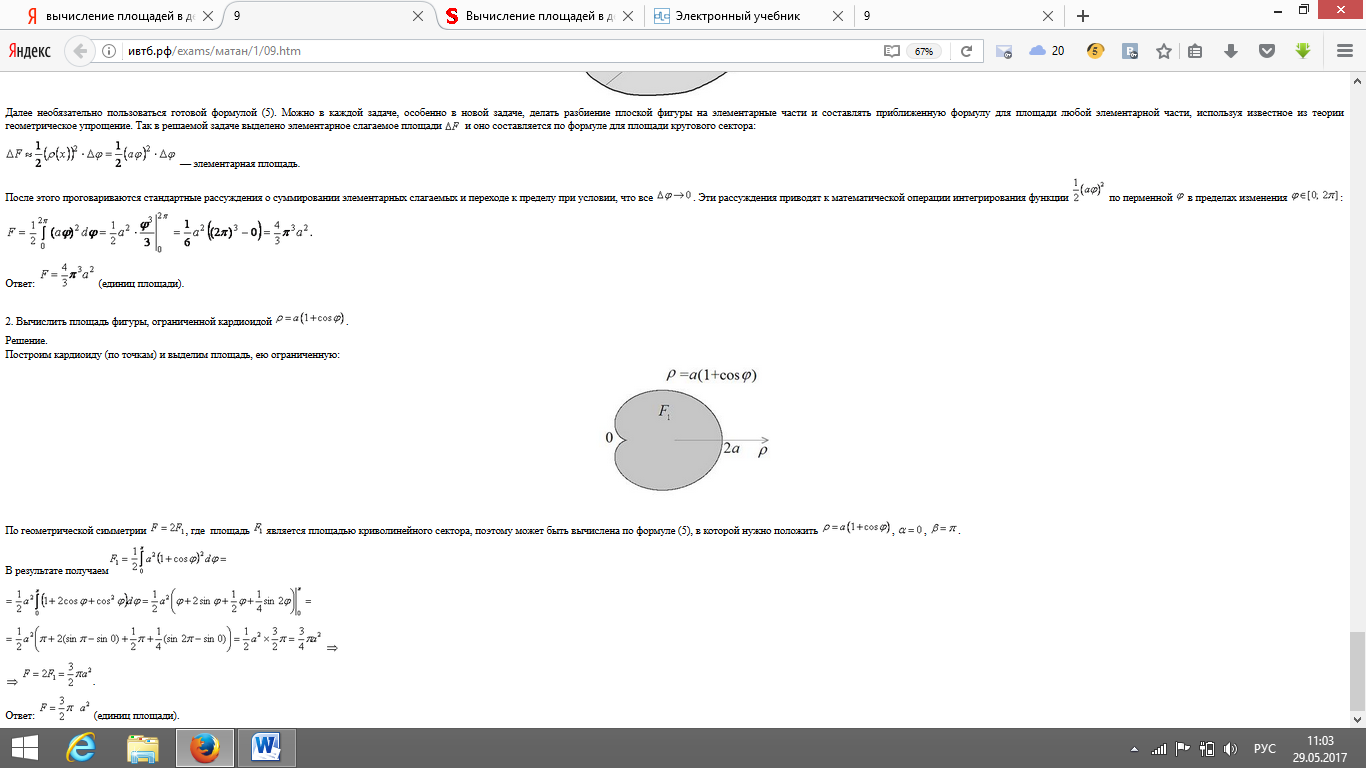
№47 Криволинейные интегралы первого рода (по длине дуги) и их основные свойства.
Определение первообразной.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 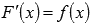 для любого х из заданного промежутка.
для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 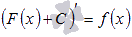 . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Определение неопределенного интеграла.
Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается 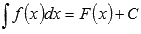 .
.
Выражение 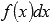 называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
1. 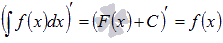
Производная результата интегрирования равна подынтегральной функции.
2. 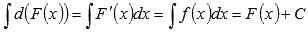
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
3. 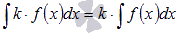 , где k – произвольная константа.
, где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.
4. 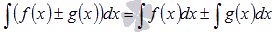
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.
Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:
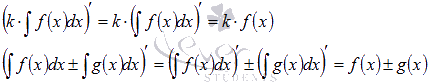
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:
· первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
· второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
Рассмотрим пример.
Пример.
Найти первообразную функции 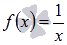 , значение которой равно единице при х = 1.
, значение которой равно единице при х = 1.
Решение.
Мы знаем из дифференциального исчисления, что 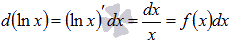 (достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом,
(достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом, 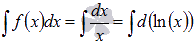 . По второму свойству
. По второму свойству 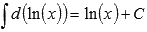 . То есть, имеем множество первообразных
. То есть, имеем множество первообразных 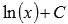 . При х = 1 получим значение
. При х = 1 получим значение 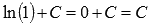 . По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид
. По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид 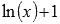 .
.
Пример.
Найти неопределенный интеграл 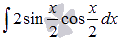 и результат проверить дифференцированием.
и результат проверить дифференцированием.
Решение.
По формуле синуса двойного угла из тригонометрии 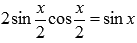 , поэтому
, поэтому
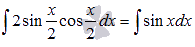
Из таблицы производных для тригонометрических функций имеем
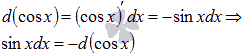
То есть, 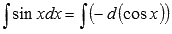
По третьему свойству неопределенного интеграла можем записать 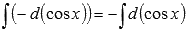
Обращаясь ко второму свойству, получим 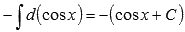 .
.
Следовательно, 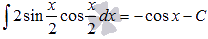
Проверка.
Для проверки результата продифференцируем полученное выражение:
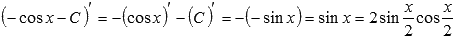
В итоге получили подынтегральную функцию, значит, интегрирование выполнено правильно. В последнем переходе была использована формула синуса двойного угла.
№2 Теорема о множестве первообразных
Теорема о множестве первообразных: Если f(x) имеет в данном промежутке первообразную F(x), то все первообразные данной функции заключены в выражении F(x) + С. Две первообразные одной функции отличаются друг от друга только на константу. Неопределенный интеграл: пусть f(x) имеет на ( a, b ) F(x), такую, что F/(x) = f(x) или dF(x) = f(x)dx, тогда F(x) + С –является общим выражением для всех первообразных и называется неопределенным интегралом от заданной функции f(x). Свойства: 1) Если f(x) непрерывна на ( a, b ), то на ( a, b ) существует F(x) и неопределенный интеграл.
№3 Внесение под знак дифференциала
При сведении заданного интеграла к табличному часто используются следующие преобразования дифференциала как операция «подведения под знак дифференциала». При этом используется формула: 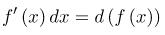
Вообще говоря, внесение (подведение) под знак дифференциала и замена переменной (метод подстановки) – это один и тот же метод нахождения неопределенного интеграла; отличие состоит только в оформлении.
Суть метода. Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то есть если 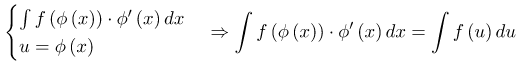
№4

№5 



№6 Интегрирование по частям.




 №7 Простейшие рациональные дроби и их интегрирование.
№7 Простейшие рациональные дроби и их интегрирование.




 №9
№9


№10


№11
1. Интегралы вида 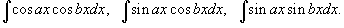 Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность: Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность: 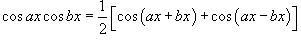 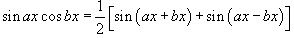 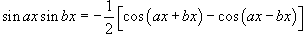 2. Интегралы вида 2. Интегралы вида 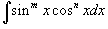 Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования: Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:
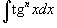 Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения 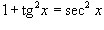 и формулы редукции и формулы редукции 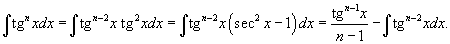 4. Интегралы вида 4. Интегралы вида 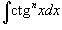 Здесь степень подынтегрального выражения понижается с помошью соотношения Здесь степень подынтегрального выражения понижается с помошью соотношения 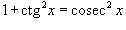 и формулы редукции и формулы редукции 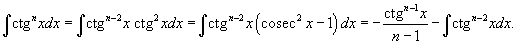 |
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы: 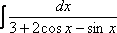 ,
, 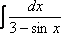 ,
, 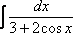 ,
, 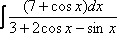 и т.д.
и т.д.
(1) Производим в исходный интеграл подстановку: 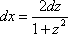 ,
, 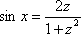 ,
, 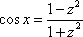 .
.
(2) Приводим знаменатель к общему знаменателю.
(3) Избавляемся от четырехэтажности дроби, при этом 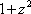 у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.
у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.
(4) Приводим подобные слагаемые в знаменателе.
(5) Интеграл 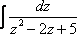 решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение
решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение 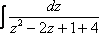 является подготовкой для осуществления вышеуказанного приёма
является подготовкой для осуществления вышеуказанного приёма
(6) Выделяем полный квадрат и готовим интеграл для интегрирования.
(7) Интегрируем по табличной формуле 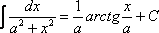 .
.
(8) Проводим обратную замену, вспоминая, что 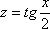 .
.
№12

№14 Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 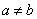 ) называется приращение какой-нибудь её первообразной на данном отрезке.
) называется приращение какой-нибудь её первообразной на данном отрезке.

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
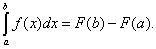 (38)
(38)
Равенство (38) называется формулой Ньютона-Лейбница.
Основные свойства:
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 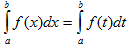 , где х, t – любые буквы.
, где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
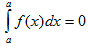
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
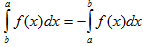
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
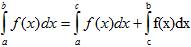
V. Постоянный множитель можно выносить за знак определенного интеграла.
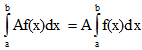
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
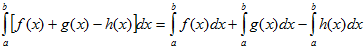
№151. Постоянный множитель можно выносить за знак определённого интеграла:
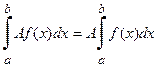 .
.
2. Если функции f(x) и g(x) интегрируемы на  , то определённый интеграл их алгебраической суммы равен алгебраической сумме интегралов от слагаемых:
, то определённый интеграл их алгебраической суммы равен алгебраической сумме интегралов от слагаемых:
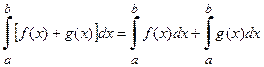 .
.
Замечание: Свойство справедливо для любого конечного числа слагаемых.
Следствие:
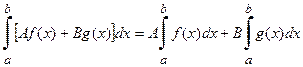
(свойство линейности операции интегрирования).
3. Если отрезок 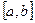 разбит точкой С на части, то интеграл по всему промежутку равен сумме интегралов по его частям (при любом расположении точек a, b, и с).
разбит точкой С на части, то интеграл по всему промежутку равен сумме интегралов по его частям (при любом расположении точек a, b, и с).
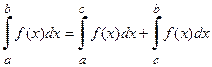
(свойство аддитивности).
№16 -17



&nbs

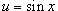 .
. .
.