Потери напора в местных сопротивлениях

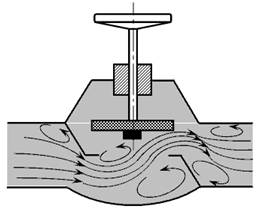
Потери напора в местных сопротивлениях зависят главным образом только от конструкции местного сопротивления. Например, при прохождении потока через вентильный кран образуется больше завихрений, следовательно, происходит больше потерь напора (энергии), чем при прохождении через пробковый кран (рис. 4.3).

а) б)

Рис. 4.3. Вихреобразование при протекании жидкости:

а) - в вентильном кране; б) - в пробковом кране

Потери напора в местных сопротивлениях h_м определяют по формуле Вейсбаха:

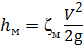, (4.10)

где ζ_м – коэффициент местного сопротивления.

Коэффициент ζ_м определяют опытным путём. В справочниках приведены полученные экспериментально значения коэффициентов для различных типов местных сопротивлений. Теоретически получена формула при внезапном расширении или сужении потока.

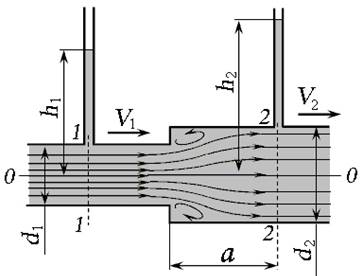
Рис. 4.4. Внезапное расширение потока

Особенностями внезапного расширения потока (рис. 4.4) являются:

- пъезометр в сечении 2 – 2 устанавливают на расстоянии а от зоны расширения для определения коэффициента ζ_вр (коэффициент сопротивления при внезапном расширении) опытным путём, так как действительная пъезометрическая высота будет только в безвихревой зоне трубопровода (в зоне сформированного основного потока);

- пъезометрическая высота в сечении 2 – 2 будет больше, чем в сечении 1 – 1 ( ).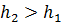

Для пояснения последнего утверждения составим уравнение Бернулли для сечений 1 – 1 и 2 – 2 относительно плоскости сравнения 0 – 0 для идеальной жидкости (то есть без учёта потерь напора), учитывая, что пъезометрическая высота :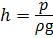

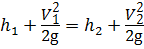. (4.11)

Так как скорость 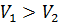(из-за разницы в площадях сечений), логично утверждать, что для сохранения равенства левой и правой частей уравнения пъезометрическая высота h₂ должна быть больше высоты h₁. В этом заключается закон сохранения энергии для идеальной движущейся жидкости – полная энергия в сечениях неизменна. Если кинетическая энергия жидкости уменьшается при переходе от одного сечения к другому, потенциальная энергия увеличивается, и наоборот.

Потери напора h_вр при внезапном расширении равны скоростному напору, соответствующему потерянной скорости (формула Борда):

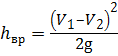, (4.12)

где (V₁ – V₂) – потерянная скорость.

Используя уравнение неразрывности потока (V₁S₁ = V₂S₂ =…= V_nS_n), можно выразить V₁ через V₂ (или наоборот), после чего формула (4.12) примет вид:

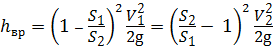. (4.13)

Отсюда видно, что коэффициент сопротивления при внезапном расширении потока, отнесённый к скорости V₁ или V₂ в соответствии с формулой (4.13), будет равен:

ζ_вр1 = 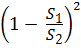или ζ_вр2 = 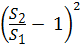. (4.14)

.

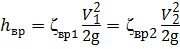Учитывая, что потери напора рассматриваются в круглоцилиндрической трубе, формулу (4.14) можно переписать в виде:

ζ_вр1 = 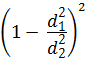или ζ_вр2 = .

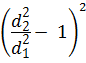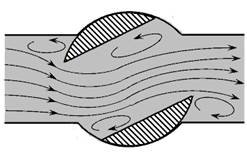
Особенностями внезапного сужения потока (рис. 4.5) являются:

- образование двух вихревых зон;

- для измерения пъезометрических напоров в сечениях пъезометры необходимо установить на расстоянии а и b от границы сужения (в зоне сформированного основного потока).

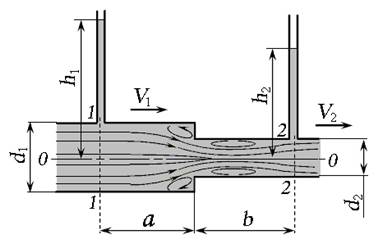
Рис. 4.5. Внезапное сужение потока

Коэффициент сопротивления ζ_вс при внезапном сужении трубы, отнесённый к скорости V₂ (скорость после сопротивления), определяют по формуле Идельчика:

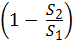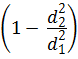ζ_вс = 0,5 = 0,5 . (4.15)

Для уменьшения сопротивления, связанного с расширением или сужением потока, применяют конусный переход от одного диаметра к другому.

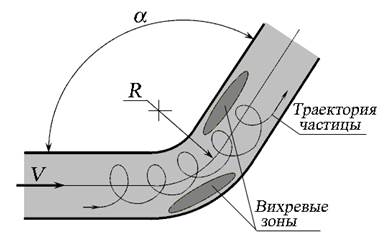
Рис. 4.6. Поворот трубопровода

Потери при повороте трубопровода зависят от угла поворота α и радиуса закругления R (рис. 4.6). Особенностью течения является поперечная циркуляция потока, в котором линии тока частиц становятся винтообразными.

Все гидроаппараты являются местными сопротивлениями. Для удобства расчётов потери напора в гидроаппаратах выражают в потерях давления ∆р, значение которого указывают в паспортных данных.

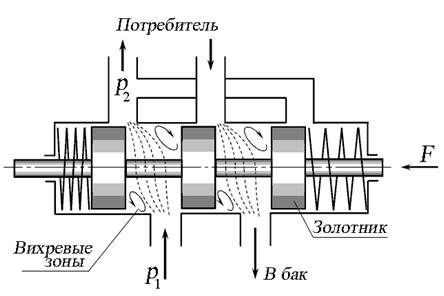
Рис. 4.7. Течение жидкости в гидрораспределителе

Рассмотрим течение жидкости через гидрораспределитель, основным элементом которого является золотник (рис. 4.7). Под действием пружин золотник занимает центральное положение, при котором гидролинии, подключённые к гидрораспределителю, перекрыты. Под действием внешней силы F золотник перемещается, открывая линии для течения жидкости. Образующиеся при этом завихрения жидкости снижают давление с р₁ до р₂. Уравнение Бернулли в этом случае примет вид:

.

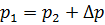В большинстве случаев течение жидкости является турбулентным. При ламинарном режиме потери в местных сопротивлениях могут быть заданы эквивалентной длиной.

Эквивалентная длина L_эк – это фиктивная длина, потери напора по которой будут равнозначны потерям в рассматриваемых местных сопротивлениях. Тогда общие потери напора определяют по формуле Пуазейля:

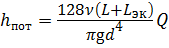. (4.16)

Структурная схема определения общих потерь напора в трубопроводе представлена на рис. 4.8.

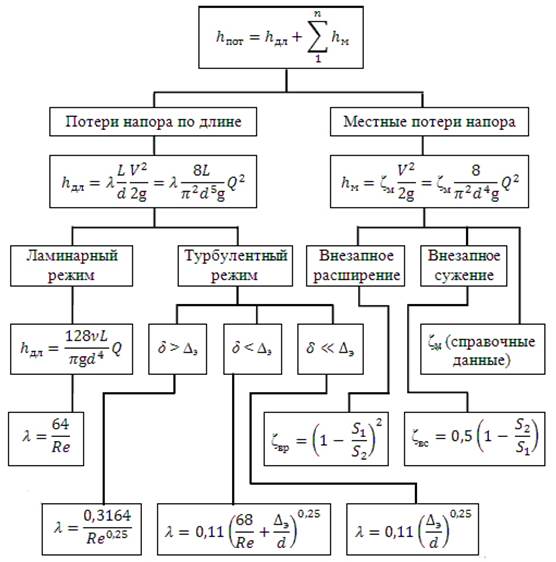
Рис. 4.8. Структурная схема к определению потерь напора

по длине и в местных сопротивлениях

Примеры решения задач

Задачи данного раздела решают с помощью уравнения расхода и уравнения Бернулли для реальной жидкости с учётом потерь напора h_пот. Необходимо помнить, что коэффициент Кориолиса для ламинарного течения жидкости равен α = 2, при турбулентном α = 1. Потери напора по длине зависят от коэффициента λ, который определяют в зависимости от соотношения толщины вязкого подслоя потока δ и эквивалентной шероховатости ∆_Э по формулам (4.6), (4.7) или (4.8). Для трубопроводов гидропривода используют формулу Блазиуса (4.6). Формулу Шифринсона (4.8) используют реже формулы Альтшуля (4.7), так как она предполагает значительный скоростной напор. Коэффициент внезапного расширения при втекании жидкости в бак ζ_вр = 1, так как 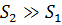. Коэффициент внезапного сужения при втекании жидкости из бака в трубопровод ζ_вс = 0,5, так как . Правила применения уравнения Бернулли приведены в п. 3.5.

Задача 4.3.1. Вода под напором движется в бак, расположенный на высоте h от оси трубопровода. Определить высоту h до уровня воды в баке, открытом в атмосферу, если вязкость воды ν = 0,01 Ст, диаметр трубопровода d = 10 мм, длина L = 20 м, пъезометрический напор в сечении 1 – 1 принять H_п = 20 м. Расход воды в трубопроводе составляет Q = 0,072 л/с. Коэффициенты сопротивления крана ζ_кр = 4, поворота ζ_пов = 1. Трубу считать гидравлически гладкой.

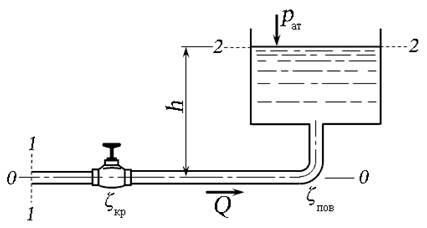
Рис. 4.9. Схема к задаче 4.3.1

Составим уравнение Бернулли для сечений 1 – 1 и 2 – 2 относительно плоскости сравнения 0 – 0. Центр тяжести сечения 1 - 1 лежит в плоскости сравнения, поэтому z₁ = 0. Пъезометрический напор в сечении 1 – 1 является пъезометрической высотой в этом сечении:

.

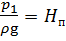В сечении 2 – 2 скорость течения воды V₂ = 0, избыточное давление р_изб = 0. Давления в сечениях определим в избыточной системе отсчёта. Коэффициент Кориолиса α = 1.

Потери напора h_пот будут равны сумме потерь напора:

- по длине 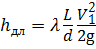, где V₁ – скорость течения воды в трубопроводе;

- местных сопротивлений .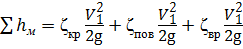

Учитывая, что ζ_вр = 1, сумма местных сопротивлений будет равна

.

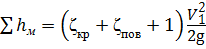Скорость в трубопроводе определим из формулы расхода:

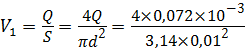= 0,917 м/с.

Определим коэффициент гидравлического трения λ по формуле Блазиуса (4.6):

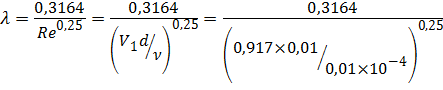= 0,0323.

Уравнение Бернулли примет вид:

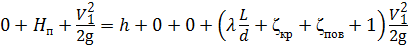, откуда

=

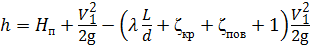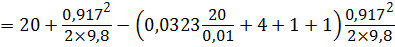= 17 м.

Задача 4.3.2. Поршень диаметром D = 200 мм движется равномерно вверх, всасывая воду. Диаметр трубопровода d = 50 мм, его длина L = 12 м, коэффициент гидравлического трения λ = 0,03, коэффициент местного сопротивления (поворота) ζ_пов = 0,5. При высоте h = 2 м сила, необходимая для перемещения поршня вверх, равна F = 2,35 кН.

Определить скорость перемещения поршня. Найти, до какой высоты h_max можно поднять поршень без возникновения кавитации, если давление насыщенного пара р_нп = 4,25 кПа, плотность воды ρ = 1000 кг/м³. Атмосферное давление принять р_ат = 98,7 кПа. Весом поршня и трением пренебречь.

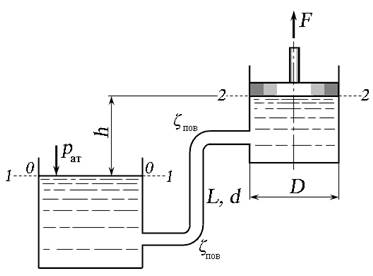
Рис. 4.10. Схема к задаче 4.3.2

Составим уравнение Бернулли для сечений 1 – 1 и 2 – 2, плоскость сравнения 0 – 0 и сечение 1 – 1 совпадают. Давления в сечениях определим в избыточной системе отсчёта.

В сечении 1 – 1 избыточное давление р_изб = 0, скорость V₁ = 0. Движение жидкости примем турбулентным, коэффициент Кориолиса α = 1.

Под поршнем (в сечении 2 – 2) создаётся вакуумметрическое давление р_вак, за счёт чего жидкость поднимается вверх. Давление р₂ = р_вак будет определяться силой F и площадью поршня S_п:

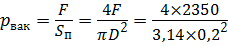= 74840 Па.

Потери напора h_пот будут равны сумме потерь напора:

- по длине 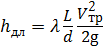, где V_тр – скорость течения воды в трубопроводе;

- местных сопротивлений .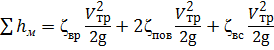

Учитывая, что ζ_вр = 1, ζ_вс = 0,5, сумма местных сопротивлений будет равна 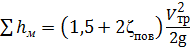. Уравнение Бернулли примет вид:

.

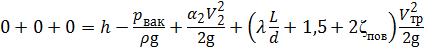С помощью уравнения расхода выразим скорость в трубопроводе:

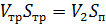, откуда .

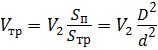Подставим выражение для скорости V_тр в составленное уравнение Бернулли:

,

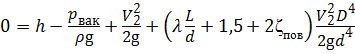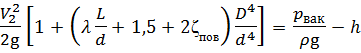, откуда

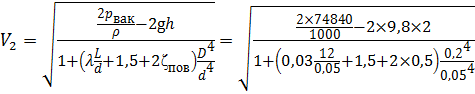= 0,21 м/с.

Наибольшую допустимую высоту подъёма поршня h_max определим из условия падения под поршнем абсолютного давления до давления насыщенного пара р_нп. Составим уравнение Бернулли в абсолютных давлениях:

,

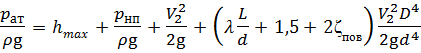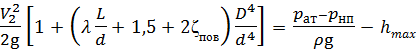, откуда

=

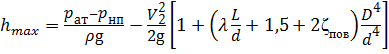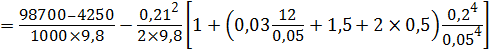= 4 м.