Уравнение Бернулли для установившегося движения

Рассмотрим движение элементарной частицы идеальной жидкости из точки 1 в точку 2, причём параметры частицы (высота положения z, давление р и местная скорость u) в точках 1 и 2 будут различны (рис. 3.6).

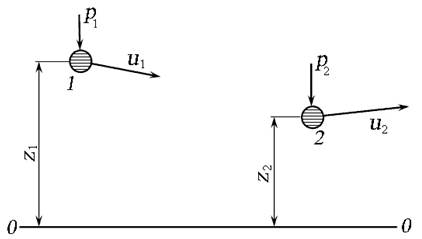
Рис. 3.6. Движение частицы идеальной жидкости

Обладая различными параметрами в точках 1 и 2, можно утверждать, что частица обладает разной по значению удельной потенциальной и кинетической энергией относительно произвольно выбранной плоскости 0 – 0, называемой плоскостью сравнения:

- удельная потенциальная энергия Е_п определяется высотой положения z (удельная энергия положения) и давлением р (удельная энергия давления)

;

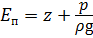- удельная кинетическая энергия Е_к определяется значением скорости движения частицы жидкости (в данном случае местной скоростью u)

.

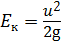Так как рассматривается движение идеальной жидкости (отсутствуют силы вязкости, соответственно, отсутствуют потери энергии при перемещении частицы из точки 1 в точку 2), значение полной энергии Е:

Е = Е₁ = Е₂,

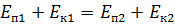. (3.6)

Уравнение (3.6) выражает закон сохранения энергии в идеальной жидкости: сумма удельной энергии положения z, удельной энергии давления 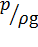и удельной кинетической энергии 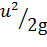для любой частицы идеальной жидкости есть величина постоянная при её перемещении из точки 1 в точку 2:

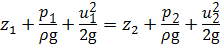. (3.7)

Уравнение (3.7) называют уравнением Бернулли для элементарной струйки идеальной жидкости. Как уже отмечалось в п. 2.3, удельную энергию называют напором. Сумма гидростатического Н_p (или пъезометрического, если р = р_изб) и скоростного H_V напоров называется гидродинамическим напором H_d:

.

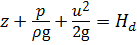Все составляющие уравнения Бернулли (3.7) имеют метрическую размерность, поэтому их можно рассматривать как высоты:

- геометрическая высота z, м;

- гидростатическая (или пъезометрическая) высота 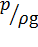, м;

- скоростная высота 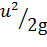, м.

Для потока реальной жидкости необходимо учесть потери энергии по пути движения жидкости, и переход от местной скорости к средней. Уравнение Бернулли для потока реальной жидкости примет вид:

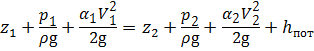, (3.8)

где h_пот – потери напора по длине потока;

α₁ и α₂ – коэффициент Кориолиса.

Потери напора h_пот возникают вследствие сил сопротивления движению, обусловленных внутренним трением в вязкой жидкости и вихреобразованию. Потери напора выражают в метрах.

Коэффициент Кориолиса α учитывает неравномерность распределения скоростей по живому сечению при переходе от действительных местных скоростей к фиктивной средней скорости потока.

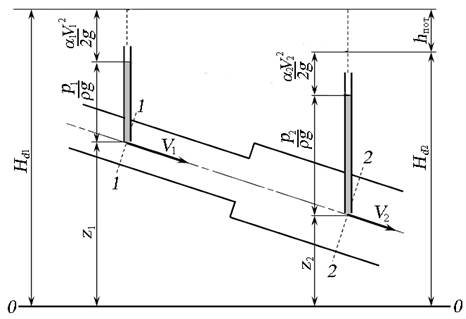
Рис. 3.7. Графическое представление уравнения Бернулли

для реальной жидкости

Поскольку все составляющие уравнения Бернулли имеют метрическую размерность, уравнение можно интерпретировать графически. Рассмотрим участок трубопровода переменного сечения (рис. 3.7). Выделим два живых сечения 1 – 1 и 2 – 2, в центре которых установим пъезометры, высота столба жидкости в которых будет пъезометрической высотой - мерой избыточного давления в сечениях. Высоты z₁ и z₂ от центров тяжести сечений до плоскости сравнения 0 – 0 будут геометрическими высотами. Значение скоростной высоты, не определяемой визуально, отложим от пъезометрической высоты. Гидродинамический напор H_d1 и H_d2 будет равен сумме геометрической, пъезометрической и скоростной высоты в сечениях 1 и 2. В соответствии с уравнением (3.8) и графическим представлением уравнения:

.
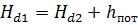