Площадь поверхности вращения
 Рассмотрим непрерывно дифференцируемую функцию
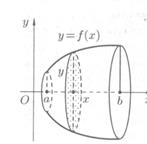
Рассмотрим непрерывно дифференцируемую функцию 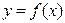 , неотрицательную на промежутке [a,b]. Пусть кривая АВ является графиком этой функции. В результате вращения этой кривой вокруг оси OX получится поверхность, изображенная на ниже приведенном рисунке.
, неотрицательную на промежутке [a,b]. Пусть кривая АВ является графиком этой функции. В результате вращения этой кривой вокруг оси OX получится поверхность, изображенная на ниже приведенном рисунке.
Если кривая АВ задана явно 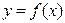
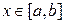 , то площадь поверхности вращения вычисляется по формуле
, то площадь поверхности вращения вычисляется по формуле
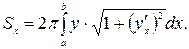
Если же кривая задана параметрически 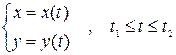 , то формула для вычисления площади примет вид
, то формула для вычисления площади примет вид
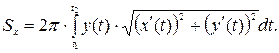
Пример 1. Найти площадь сферы радиуса 4.
Так как сфера может рассматриваться как результат вращения полуокружности радиуса 4, лежащей в верхней полуплоскости, вокруг оси OX , то необходимо сначала задать аналитически эту полуокружность: 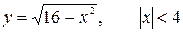 .
.
Для описания кривой мы использовали явное задание функции, следовательно, для вычисления площади поверхности вращения выберем формулу вида 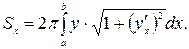
При перемещении точки по полуокружности аргумент 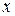 изменяется в промежутке [-4;4], поэтому пределы интегрирования будут изменяться в тех же границах. Следовательно,
изменяется в промежутке [-4;4], поэтому пределы интегрирования будут изменяться в тех же границах. Следовательно,
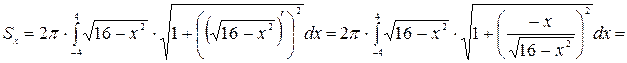
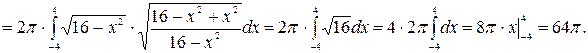 Заметим, что аналогичный результат может быть получен при вращении полуокружности, лежащей в правой полуплоскости, вокруг оси OY. Следовательно, полученный результат является площадью любой сферы радиуса 4.
Заметим, что аналогичный результат может быть получен при вращении полуокружности, лежащей в правой полуплоскости, вокруг оси OY. Следовательно, полученный результат является площадью любой сферы радиуса 4.
Пример 2. Найти площадь поверхности, образованной вращением первой арки циклоиды вокруг оси OX.
Так как циклоида задается параметрическим уравнением вида 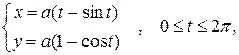 то для вычисления площади поверхности вращения используем формулу
то для вычисления площади поверхности вращения используем формулу 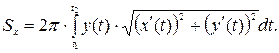 Для начала вычислим производные координат
Для начала вычислим производные координат 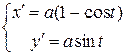 , а затем подставим эти результаты в подынтегральное выражение, получим
, а затем подставим эти результаты в подынтегральное выражение, получим
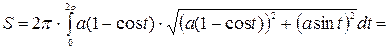
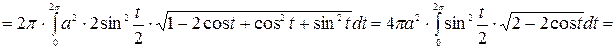
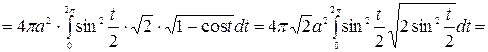
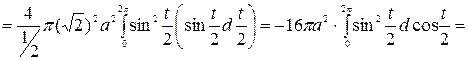
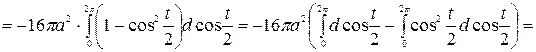

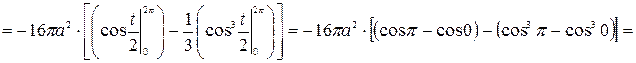
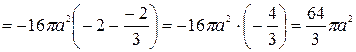 .
.
Экономический смысл определенного интеграла
Рассмотрим применение определенного интеграла к решению некоторых экономических задач.
1) Пусть функция f(t) показывает зависимость производительности производства от времени x . Тогда объем выпускаемой этим производством продукции за период x 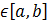 численно равен определенному интегралу
численно равен определенному интегралу 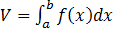 .
.
2) Пусть функция f(x) характеризует поступление продукции на склад от времени, тогда запас продукции на складе за T дней равно 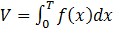 .
.
3) Если спрос на некоторый товар задается функцией p=p(q) , где q – количество товара в ед., а p – цена единицы товара. Тогда величина потребительского излишка за промежуток времени q 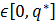 определяется как CS
определяется как CS 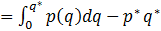 , где
, где 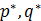 - значения, при которых достигается равновесие на рынке.
- значения, при которых достигается равновесие на рынке.
ЗАДАЧИ
2.1.1. Найти площадь фигуры, ограниченной линиями:  .
.
2.1.2. Найти площадь фигуры, ограниченной линиями: 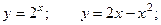
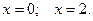
2.1.3. Найти площадь фигуры, ограниченной линиями: 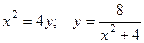 .
.
2.1.4. Найти площадь фигуры, ограниченной линиями 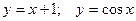 и осью ОХ.
и осью ОХ.
2.1.5. Найти площадь фигуры, лежащей в первом квадранте и ограниченной линиями 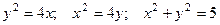 .
.
2.1.6. Найти площадь между параболой 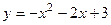 , касательной к ней в точке М(2;-5) и осью ординат.
, касательной к ней в точке М(2;-5) и осью ординат.
2.1.7. Найти площадь фигуры, заключенной между параболой 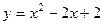 , касательной к ней в точке М(3;5) и осью ординат.
, касательной к ней в точке М(3;5) и осью ординат.
2.1.8. Найти площадь фигуры, заключенной между параболой 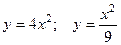 и прямой
и прямой 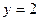 .
.
2.1.9. Окружность 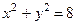 разделена параболой
разделена параболой 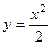 на две части. Найти площадь обеих частей.
на две части. Найти площадь обеих частей.
2.1.10. Найти площадь фигуры, ограниченной линиями 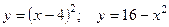 и осью ОХ.
и осью ОХ.
2.1.11. Найти площадь фигуры, лежащей в первом квадранте и ограниченной линиями 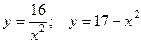 .
.
2.1.12. Найти площадь фигуры, ограниченной одной аркой циклоиды 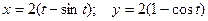 .
.
2.1.13. Найти площадь фигуры, ограниченной астроидой 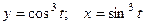 .
.
2.1.14. Найти площадь фигуры, ограниченной эллипсом 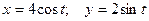 .
.
2.1.15. Найти площадь фигуры, ограниченной кардиоидой 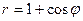 .
.
2.1.16. Найти площадь фигуры, ограниченной кривой 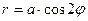 .
.
2.1.17. Найти площадь фигуры, ограниченной кривой 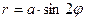 .
.
2.1.18. Найти площадь фигуры, лежащей вне круга 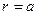 и ограниченной кривой
и ограниченной кривой 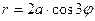 .
.
2.1.19. Найти площадь фигуры, ограниченной линиями 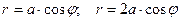 .
.
2.1.20. Найти площадь фигуры, ограниченной линиями 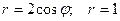 , лежащей вне круга
, лежащей вне круга 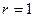 .
.
2.2.1. Вычислить объем тела, образованного вращением вокруг оси ОХ площади, ограниченного осями координат и кривой 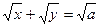 .
.
2.2.2. Фигура, ограниченная дугой синусоиды 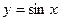 , осью ординат и прямой
, осью ординат и прямой 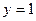 , вращается вокруг оси OY. Определить объем полученного тела вращения.
, вращается вокруг оси OY. Определить объем полученного тела вращения.
2.2.3. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболой 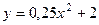 и прямой
и прямой 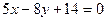 .
.
2.2.4. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами 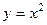 и
и 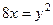 .
.
2.2.5. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 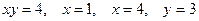 , вокруг оси ОХ.
, вокруг оси ОХ.
2.2.6. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 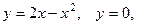 вокруг оси ОХ.
вокруг оси ОХ.
2.2.7. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 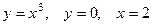 , вокруг оси OY.
, вокруг оси OY.
2.2.8. Вычислить объем тела, образованного вращением одной волной кривой 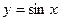 , осью ОХ, вокруг оси OХ.
, осью ОХ, вокруг оси OХ.
2.2.9. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 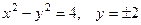 , вокруг оси ОY.
, вокруг оси ОY.
2.2.10. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 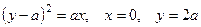 , вокруг оси ОХ.
, вокруг оси ОХ.
2.2.11. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 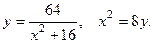
2.2.12. Найти объем тела, образованного при вращении вокруг оси ОХ кривой 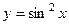 в промежутке от
в промежутке от 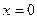 до
до 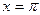 .
.
2.2.13. Найти объем тела, образованного вращением фигуры, ограниченной полукубической параболой 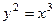 , осью ОХ и прямой
, осью ОХ и прямой 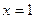 , вокруг оси ОХ.
, вокруг оси ОХ.
2.2.14. Вычислить площадь поверхности, образованной вращением части кривой 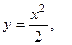 прямой
прямой 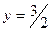 вокруг оси OY.
вокруг оси OY.
2.2.15. Вычислить площадь поверхности, образованной вращением части кривой 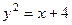 , отсеченной прямой
, отсеченной прямой 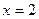 , вокруг оси OX.
, вокруг оси OX.
2.2.16. Вычислить площадь поверхности, образованной вращением дуги цепной линии 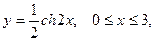 вокруг оси ОХ.
вокруг оси ОХ.
2.2.17. Вычислить площадь поверхности, образованной вращением одной полуволны кривой 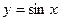 вокруг оси ОХ.
вокруг оси ОХ.
2.2.18. Определить площадь поверхности, образованной вращением дуги кривой 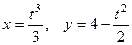 между точками пересечения с осями координат, вокруг оси ОХ.
между точками пересечения с осями координат, вокруг оси ОХ.
2.2.19. Вычислить площадь поверхности, образованной вращением вокруг оси ОХ дуги кривой 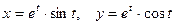 от
от 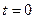 до
до 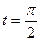 .
.
2.2.20. Вычислить площадь поверхности, образованной вращением вокруг оси ОХ дуги кривой 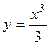 от
от 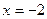 до
до 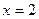 .
.
2.3.1. Вычислить длину дуги полукубической параболы 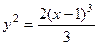 , заключенной внутри параболы
, заключенной внутри параболы 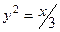 .
.
2.3.2. Вычислить длину дуги кривой 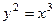 , отсеченной прямой
, отсеченной прямой 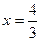 .
.
2.3.3. Вычислить длину дуги кривой 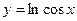 , заключенной между точками с абсциссами
, заключенной между точками с абсциссами 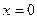 и
и 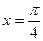 .
.
2.3.4. Вычислить длину дуги кривой 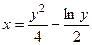 , заключенной между точками с ординатами
, заключенной между точками с ординатами 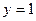 и
и 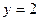 .
.
2.3.5. Вычислить длину дуги кривой 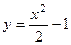 , отсеченной осью ОХ.
, отсеченной осью ОХ.
2.3.6. Вычислить длину дуги кривой 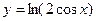 между соседними точками пересечения с осью ОХ.
между соседними точками пересечения с осью ОХ.
2.3.7. Вычислить длину дуги полукубической параболы 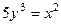 , заключенной внутри окружности
, заключенной внутри окружности 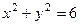 .
.
2.3.8. Вычислить длину дуги кривой 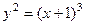 , отсеченной прямой
, отсеченной прямой 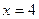 .
.
2.3.9. Вычислить длину дуги кривой 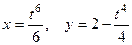 , заключенной между точками пересечения с осями координат.
, заключенной между точками пересечения с осями координат.
2.3.10. Вычислить длину дуги кривой 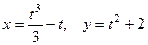 от
от 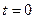 до
до 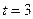 .
.
2.3.11. Вычислить длину дуги кривой 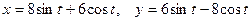 от
от 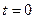 до
до 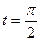 .
.
2.3.12. Вычислить длину дуги кривой 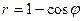 .
.
2.3.13. . Вычислить длину дуги кривой 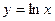 от
от 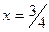 до
до 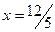 .
.
2.3.14. . Вычислить длину первого завитка спирали 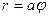 .
.
2.3.15. . Вычислить длину дуги кардиоиды 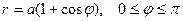 .
.
2.3.16. Определить длину дуги кривой 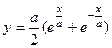 между прямыми
между прямыми 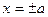 .
.
2.3.17. . Вычислить длину дуги кривой 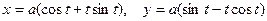 от
от 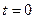 до
до 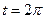 .
.
2.3.18. . Вычислить длину дуги астроиды 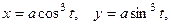
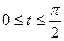 .
.
2.3.19. . Вычислить длину дуги линии 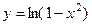 от
от 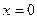 до
до 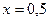 .
.
2.3.20. Найти длину дуги параболы 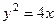 от вершины до точки М(1,2).
от вершины до точки М(1,2).
ГЛАВА 3. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
В главе 2 при введении понятия определенного интеграла особое внимание было уделено тому, что подынтегральная функция f(x) должна быть кусочно-непрерывной на промежутке [a,b], при этом и на концы промежутка накладывались ограничения 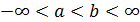 . Если нарушено хоть одно из этих двух условий, то интеграл
. Если нарушено хоть одно из этих двух условий, то интеграл 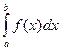 превращается в несобственный. Нарушение каждого из условий определяет свой тип несобственного интеграла. Рассмотрим отдельно каждый из них.
превращается в несобственный. Нарушение каждого из условий определяет свой тип несобственного интеграла. Рассмотрим отдельно каждый из них.
