Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки идеальной жидкости

Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и 2-2. Площади живых сечений потока обозначим dω₁ и dω_2. Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0 - 0характеризуется величинами z₁ и z₂. Давления и скорости жидкости в этих сечениях имеют значения P₁, P₂ и u_1, u₂ соответственно.

Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.

З а малый промежуток времениdt частицы жидкости из 1-1переместятся в 1'-1' на расстояние, равное u₁dt, а частицы из 2-2 в 2' - 2' на расстояние u₂dt.

Согласно теореме кинетической энергии приращение энергии тела (в данном случае выделенного объёма жидкости) равно сумме работ всех действующих на него сил.

Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести. Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки. Она будет равна произведению силы p₁dω₁ на путь u₁dt:

.

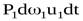Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение

.

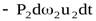Полная работа, выполненная силами давления, примет вид:

.

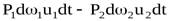Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их веса dG:

.

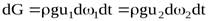При перетекании от сечения 1-1 в сечение 2-2 центр тяжести выделенного объёма переместится на разность высот (z₁ – z₂) и работа, произведённая силами тяжести, составит:

.

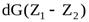Проанализируем теперь изменение кинетической энергии рассматриваемого объёма элементарной струйки жидкости.

Приращение кинетической энергии выделенного объёма за dt равно разности его кинетических энергий в сечениях 1-1 и 2-2. Это приращение составит

.

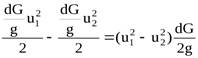Приравнивая приращение кинетической энергии сумме работ сил тяжести и сил давления, придём к виду:

.

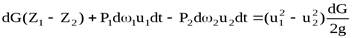Разделив обе части на вес dG, т.е. приведя уравнение к единичному весу, получим

.

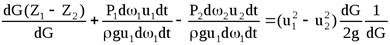После сокращения и преобразований придём к искомому виду

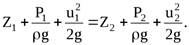
Если учесть, что сечения 1-1 и 2-2 выбраны произвольно, можно прийти к выводу, что сумма приведённых выше величин 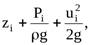описывающих движение жидкости под действием сил давления и сил тяжести есть величина постоянная для элементарной струйки, т.е.

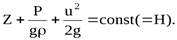
Таким образом, снова получено то же (ранее полученное интегрированием уравнений Эйлера)уравнение Бернулли для элементарной струйкиневязкой жидкости при установившемся движении под действием сил тяжести.

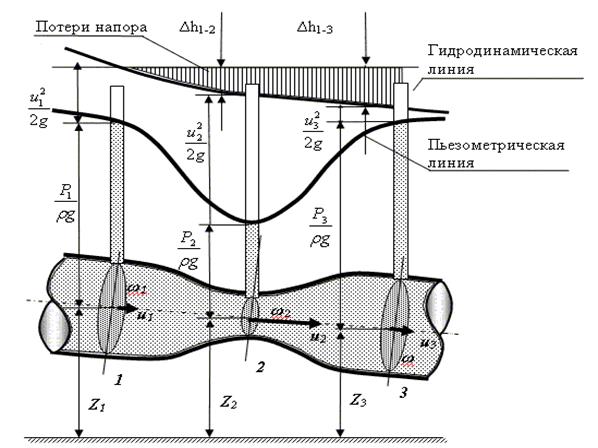
Геометрическая интерпретация уравнения Бернулли

Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

• Как и в гидростатике, величину Z называют нивелирной высотой.
• Второе слагаемое - 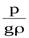носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.
• Сумма первых двух членов уравнения 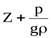¾гидростатический напор.
• Третье слагаемое в уравнения Бернулли 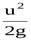называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.
• Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

В се слагаемые уравнения Бернулли имеют размерность длины и их можно изобразитьграфически.

Значения 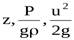-нивелирную, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое место точек, высоты которых равны 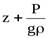, называетсяпьезометрической линией. Если к этим высотам добавить скоростные высоты, равные 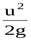, то получится другая линия, которая называетсягидродинамической или напорной линией.

Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.

Энергетическая интерпретация уравнения Бернулли

Выше было получено уравнение Бернулли с использованием э нергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамическийнапор.

С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.

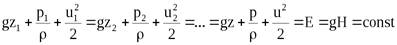
Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) gz — удель­ная потенциальная энергия положения; Р/r — удельная потенциальная энергия давления; gz + Р/r — удельная потенциальная энергия; u²/2 — удельная кинети­ческая энергия; и — скорость элементарной струйки идеальной жидкости.

Умножив все члены уравнения на удельный вес жидкости g, получим

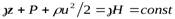
gz - весовое давление, Па; P — гидродинамическое давление, Па; rи² /2— динамическое давление Па; gH— полное давление, Па

Уравнение Бернулли для потока идеальной жидкости

П оток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек u_S, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки 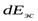равна:

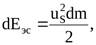
где 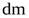- масса жидкости плотностью 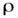, протекающей через живое сечение элементарной струйки 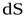со скоростью 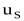за времяdt, равная:

.

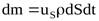Проинтегрировав выражение для 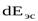, получим выражение для кинетической энергии потока идеальной жидкости .

.

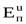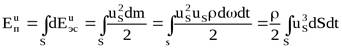Если принять, что t=1, получим:

.

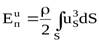Последняя формула определяет энергию потока с использованием скоростей элементарных струек u_ω.

Если получить значение кинетической энергии потока с использованием значения средней скорости потока V , получим формулу:

,

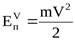где 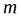- масса жидкости плотностью 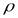, протекающей через живое сечение потока 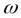со скоростью 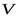за времяt, равная:

.

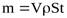После подстановки при t=1 окончательно получим:

.

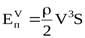Отношение 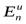и 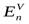, равное:

.

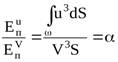Полученная величина α носит наименование коэффициента кинетической энергии или коэффициента Кориолиса.Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более.

Учитывая коэффициент кинетической энергии, приведём уравнение Бернулли для потока идеальной жидкости, которое примет вид:

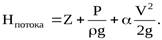
Надо учесть, что в общем случае в разных сечениях потока коэффициент α будет иметь различные значения.

Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока H_потока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напораΔh составят:

,

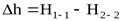где H_1-1- напор в первом сечении потока жидкости,

H_2-2 - напор во втором сечении потока,

∆h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

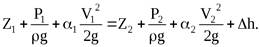
Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклонI, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

.

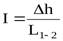Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости(закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор 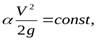а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.

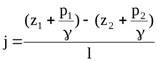
Если гидравлический уклон всегда положителен, то пьезомет­рический может быть и положительным, и отрицательным. При равномерном движении жидкости, когда скорость по длине потока не изменяется, скоростной напор вдоль потока av² / (2g) = const. Следовательно, пьезометрическая линия параллельна энергети­ческой, и пьезометрический уклон равен гидравлическому.

Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, назы­вают геометрическим уклоном i и определяют по формуле

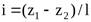
где l — расстояние между сечениями потока.

Сформулируем два условия применимости к потоку жидкости уравнения Бернулли: 1) движение жидкости должно быть установившимся; 2) движение жидкости в сечениях 1—2, 2—2 и 3—3,cоединяемых уравнением Бернулли, должно быть параллельно струйным или плавноизменяющимся, в промежутке же между сечениями 1—1, 2—2 и 3—3 движение жидкости может быть и резко меняющимся.

Hа применении уравнения Бернулли основан принцип действия приборов для измерения скоростей и расходов жидкости. Одним из таких приборов является расходомер Вентури, состоящий из двух конических отрезков трубы, узкие концы которых соединены коротким цилиндрическим патрубком длиной менее 10 диаметров трубопровода (отношение диаметра конфузора и диффузора соответственно d/D=^:0,3...0,7).Принцип работы расходомера Вентури базируется на уравнении Бернулли и уравнении неразрывности потока, а также на том, что перепад давлений на диафрагме, измеряемый пьезометром либо дифманометром пропорционален квадрату протекающего через нее расхода

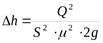
Для определения местных скоростей при плавноизменяющемся безнапорном движении применяют метод Пито. Трубку, нижний конец которой изогнут под прямым углом, опускают навстречу потоку, и жидкость в трубке начинает подниматься над свободной поверхностью, где давление равно атмосферному, на высоту .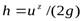

При определении местных скоростей в напорном потоке используют систему из двух трубок, одна из которых представляет собой обычный пьезометр, показывающий напор Р/g, а другая,только что описанная, измеряет величину напора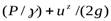

Разность уровней в обеих трубках h представляет собой скоростной напор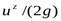

Местные скорости находят с помощью трубки Пито по формуле

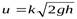
где k- поправочный коэффициент, определяемый для каждой трубки опытным путем

Различают два вида потерь напора:

потери напора на преодоление гидравлических сопротивлений по длине 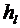, вызываемых трением жидкости о стенку трубы и слоев жидкости друг о друга;

местные потери напора 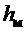, возникающие только в отдельных местах потока, где наблюдается его деформация (задвижка, поворот, резкое сужение или расширение трубы и т.п.).

Общую величину потерь напора для участка трубопровода, заключенного между двумя сечениями, определяют как сумму потерь напора по длине рассматриваемого участка и всех местных потерь напора

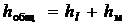. (4.1)

Потери напора для плавноизменяющегося движения определяются из уравнения Бернулли (3.11)

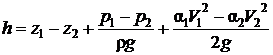. (4.2)

Из выражения (4.2) следует, что для определения общих потерь напора необходимо измерить разности геометрических, пьезометрических и скоростных напоров. При равномерном потоке в горизонтальной трубе 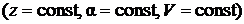потери напора определяются по формуле

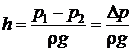, (4.3)

т.е. потери напора определяются как разность показаний пьезометров в крайних сечениях участка трубопровода.

4.2. МЕТОД ТЕОРИИ РАЗМЕРНОСТЕЙ И ЕГО ПРИЛОЖЕНИЕ К ВЫВОДУ
ОБЩИХ ФОРМУЛ ДЛЯ ОПРЕДЕЛЕНИЯ ПОТЕРЬ НАПОРА

Метод теории размерностей широко применяется во многих исследованиях. Начало общей теории этого метода было положено в 1911 г. русским ученым А. Федерманом, доказавшим фундаментальную теорему подобия, частным случаем которой является теорема о размерности, известная под названием " 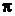-теорема". Согласно этой теореме, всякое уравнение, выражающее некоторую физическую закономерность и потому не зависящее от выбора системы единиц измерения, связывающее между собой k физических величин, среди которых n величин обладают независимыми размерностями, может быть преобразовано в уравнение, связывающее k-n независимых безразмерных комплексов, составленных из упомянутых k физических величин.

При установившемся движении жидкости средняя скорость течения V и перепад давлений 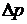зависят от физических свойств жидкости, размеров трубопровода, в котором происходит изучаемое движение жидкости, и шероховатости стенок трубы.

Физические свойства жидкостей определяются такими размерными характеристиками, как плотность 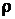и вязкость m размеры трубопровода - диаметром d и длиной l, а шероховатость стенок трубы оценивается средним значением линейных размеров выступов шероховатости .

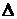Взаимосвязь между перечисленными параметрами можно выразить в виде уравнения

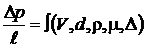, (4.4)

где 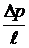- потери давления на единицу длины трубы.

В выражении (4.4) выделим три основные величины V, d, 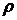с независимыми размерностями. Размерность любой из этих величин нельзя получить из комбинации размерностей двух других, в то же время через размерности V, d и 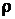можно выразить размерность любой другой величины, входящей в рассматриваемую зависимость.

1. Потери напора по длине. Формула Дарси-Вейсбаха. Местные потери.

2. Коэффициент гидравлического трения при различных режимах движения жидкости. График Никурадзе.

3. Скорость при равномерном движении жидкости.

Как отмечалось выше при движении потока реальной жидкости, ограниченного твердыми стенками, возникают потери напора, вызванные сопротивлениями двух видов: сопротивлениями по длине, обусловленными силами трения; местными сопротивлениями, обусловленными изменениями скорости потока по величине и направлению в связи с различными препятствиями, встречающимися на пути потока.

При проведении расчетов по определению потерь напора используют принцип наложения потерь, когда общие потери напора с определенными допущенными рассматривают как сумму потерь напора вызываемых каждым видом сопротивлений отдельности:

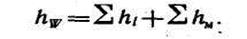
Чему же равен каждый из видов потерь напора, входящих в уравнение и как их можно определить?

Р 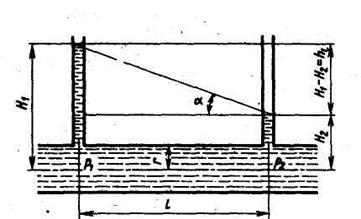ассмотрим потери напора на трение. Возьмем участок горизонтальной трубы, по которому движется жидкость.

Рисунок 20 - К определению потерь напора на трение.

В 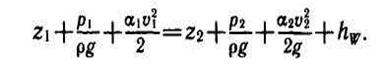ыделим два сечения и напишем для них уравнение Бернулли с учетом, что движение в трубе равномерное, а местные сопротивления отсутствуют, т. е.hw = h_l:

Следующее уравнение

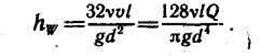называется формулой Пуазейля и служит для определения потерь напора на трение при ламинарном течении жидкости в круглой трубе. Умножив

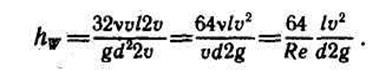числитель и знаменатель уравнения на 2ν, получим новое выражение потерь на трение:

Введя обозначение

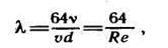п 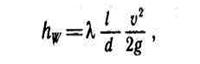олучим уравнение Дарси-Вейсбаха для определения потерь напора на трение в круглых трубах:

где к — безразмерная величина, называемая коэффициентом гидравлического сопротивления. Коэффициент показывает, какая часть напора расходуется на преодоление гидравлического трения.

З 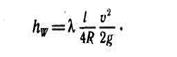аменив в уравнении диаметр на гидравлический радиус (d=4R), получим уравнение Дарси-Вейсбаха для определения потерь на трение в некруглых трубах и открытых руслах:

Формулы Дарси-Вейсбаха применимы и для турбулентного движения. В этом случае коэффициент гидравлического трения будет иметь иное значение, определяемое по другим зависимостям.

П 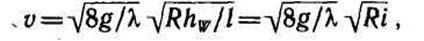реобразуя уравнение относительно скорости потока, получим:

г 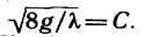де

Коэффициент С введен Шези и назван его именем. Уравнение легко преобразуется в формулу Шези:

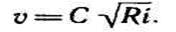Зависимость коэффициента гидравлического сопротивления от различных факторов.

При турбулентном режиме коэффициент находят по эмпирическим формулам или с помощью графиков, построенных на основе экспериментальных данных. Выяснению влияния различных факторов на значение коэффициента λ посвящено большое количество экспериментальных и теоретических работ. Рассмотрим опыты Никурадзе, выполненные еще в 1932 г. и не утратившие своего значения до настоящего времени.

Содержание опытов заключалось в следующем. На внутреннюю поверхность труб разного диаметра наклеивали зерна песка, создавая искусственную однородную шероховатость. В трубах с полученной таким образом шероховатостью при разных расходах измеряли потери напора и по формуле рассчитывали коэффициент λ. Затем строили графики зависимости коэффициента λ от числа Рейнольдса Re и от шероховатости D. Такой график показан на рисунке.

На графике на оси абсцисс отложены значения lg Re, а на оси ординат — значения lg (100 λ).

Кривые построены по точкам, представляющим усредненные значения относительной шероховатости труб: ε =D / d. Анализируя график, можно выделить характерные области.

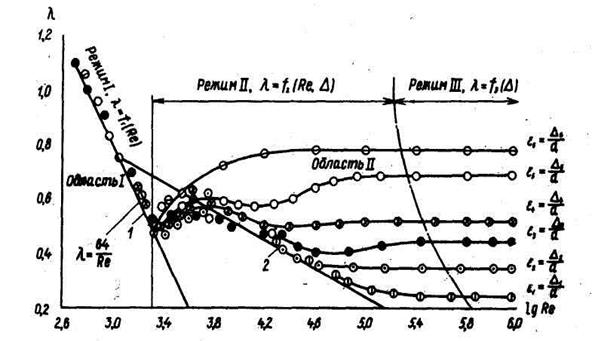Рисунок 21 - Зависимость коэффициента гидравлического сопротивления λ от числа R_E и от шероховатости.

Необходимо подчеркнуть, что опытные зависимости Никурадзе, полученные для цилиндрических труб, были подтверждены другими исследователями для напорных и безнапорных потоков с расчетов нет необходимости различать жидкости разного рода, а нужно рассматривать жидкость, всеобъемлющей характеристикой которой является число Рейнольдса.

Местные сопротивления и потери напора на их преодоление.

Движение жидкости по трубам и другим руслам связано с преодолением различных препятствий. Так, простые трубопроводы представляют собой последовательное соединение труб одного или различных диаметров. В местах соединения труб различных диаметров имеются переходные муфты. В трубопроводах могут быть повороты, внезапные и постепенные сужения, запорная арматура в виде кранов, вентилей, задвижек и др. Все эти местные включения оказывают сопротивление потоку жидкости, протекающему по трубопроводу. препятствия, встречающиеся на пути движения потока жидкости, которые вызывают изменение скорости потока либо по величине, либо направлению, либо одновременно и по величине, и по направлению.

Потери напора от местных сопротивлений особенно ощутимы, если трубопроводы составлены из коротких участков, часто изменяющих направление, имеющих изгибы, насыщенных различными местными включениями. Такие трубопроводы особенно распространены в маслопроводах гидросистем автомобилей, тракторов, самолетов, а также в водопроводных системах жилых зданий, промышленных цехов.

В учебной и справочной литературе приводятся эмпирические формулы определения коэффициента x для различных местных сопротивлений, имеются таблицы значений коэффициентов x в зависимости от вида местного сопротивления.

Лекция 11. Гидравлический удар в трубопроводах