Интегрирование рациональных функций

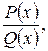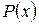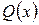Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют рациональные функции, т. е. функции, которые можно представить в виде дроби где , – многочлены. Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то, выполнив деление, получим

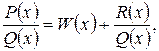
где 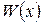– некоторый многочлен, a 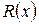– многочлен степени ниже, чем 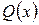. Например,

;

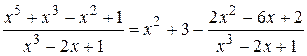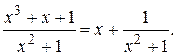
В высшей алгебре доказывается, что каждый многочлен может быть представлен в виде произведения

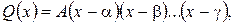
где 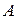— коэффициент при старшей степени многочлен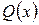а , а 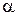, , 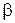..., 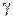— корни уравнения 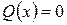. Множители ( 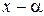)( )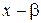...( ) 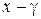называются элементарными множителями. Если среди них имеются совпадающие множители, то, группируя, получаем представление

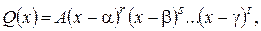
где 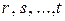– целые числа, которые называются соответственно кратностями корней 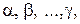причем 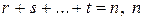– степень многочлена .

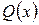Среди корней представления 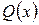могут быть и комплексные. В алгебре доказывается, что если 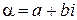– 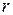-кратный комплексный корень многочлена с вещественными коэффициентами, то этот многочлен имеет также сопряженный с 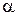r-кратный корень 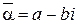. Другими словами, если в представление 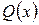входит множитель 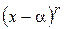, где 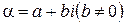, то оно содержит также и множитель 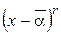. Перемножив эти два множителя, получим

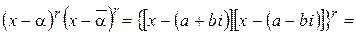
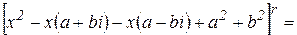
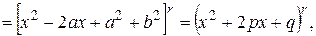
где 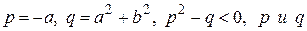– вещественные числа.

Поступая аналогично с остальными комплексными корнями, запишем

(?)

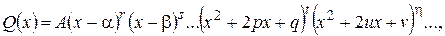где 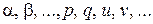— вещественные числа.

В высшей алгебре доказывается следующая теорема: если рациональная функция 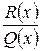имеет степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен 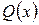представлен в виде (?), то эту функцию можно единственным образом представить в виде

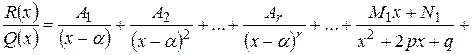
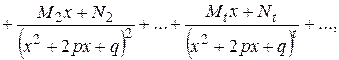
где 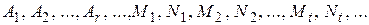– некоторые вещественные числа.

Это выражение называется разложением рациональной функциинаэлементарные дроби. Равенство имеет место для всех 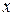, не являющихся вещественными корнями многочлена .

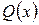Чтобы определить числа 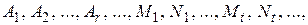умножим обе части разложения с неизвестными пока 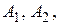... на 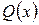. Поскольку равенство между многочленом 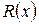и многочленом, который получится в правой части, должно быть справедливо для всех 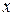, то коэффициенты, стоящие при равных степенях 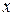, должны быть равны между собой. Приравнивая их, получаем систему уравнений первой степени, из которой найдем неизвестные числа ...

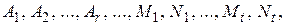Такой метод отыскания коэффициентов разложения рациональной функции называется методом неопределенных коэффициентов.

Пример. Разложить рациональную функцию 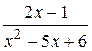на элементарные дроби.

Решение. Так как 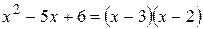, тогда имеем

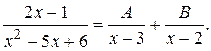
Умножая обе части равенства на 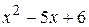, получаем

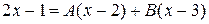, или .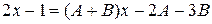

Приравнивая коэффициенты при одинаковых степенях 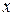, получаем систему уравнений первой степени относительно 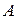и :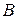

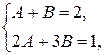
откуда 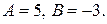Таким образом,

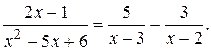
Пример. Найти разложение рациональной функции 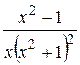на элементарные дроби.

Решение. Квадратный трехчлен 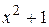имеет комплексные корни, поэтому имеем

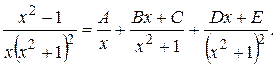
Умножая обе части равенства на 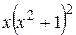, получаем

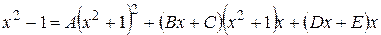
или

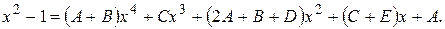
Приравнивая коэффициенты при 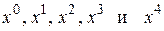, придем к системе уравнений

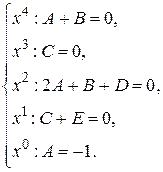
решая которую найдем А = –1, В=1, С=0, D =2, 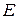=0, и поэтому искомое разложение имеет вид

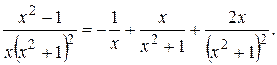
Из изложенного следует, что задача интегрирования рациональной функции сводится к интегрированию многочлена 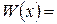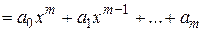, интеграл от которого является табличным:

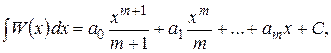
и интегрированию рациональной функции 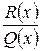, что приводит к нахождению интегралов следующих четырех типов:

I.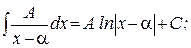

II.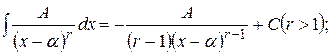

III.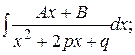

IV.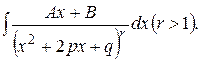

При этом многочлен 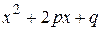не имеет вещественных корней, так что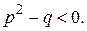

Вычислим интеграл III типа, который часто встречается на практике. Выделим из трехчлена в знаменателе полный квадрат

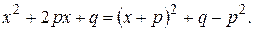
Это представление «подсказывает» подстановку 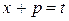, откуда 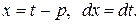Положим далее 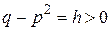и перейдем к переменной 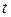. В результате интеграл преобразуется к виду

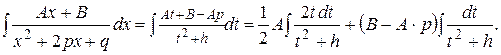
Первый интеграл в правой части берется непосредственно

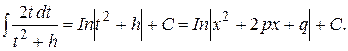
Второй интеграл является табличным.

Пример. Вычислить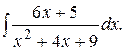

Решение. Выделим в знаменателе полный квадрат: 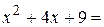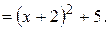Сделаем подстановку 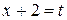, откуда 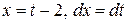, поэтому

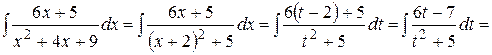
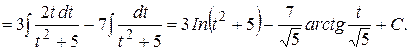
Возвращаясь к переменной 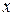, получаем

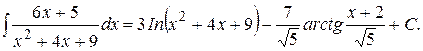
Вычислим теперь интеграл IV типа: 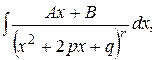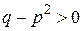, 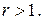Для этого введем новую переменную 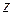по формуле 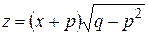, откуда

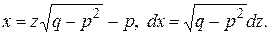
Далее, имеем

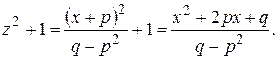
Таким образом, получаем

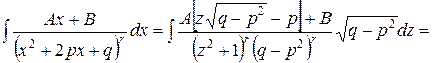
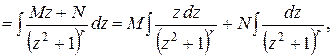
где М и N — числа, значения которых ясны из предпоследнего равенства.

Ко второму интегралу можно применить рекуррентную формулу, полученную ранее. Положив в первом интеграле 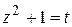, получим

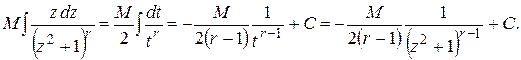
Пример. Вычислить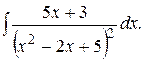

Решение. Положим 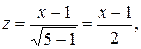откуд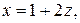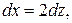а а 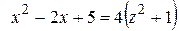, следовательно,

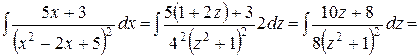
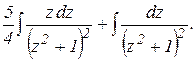
Ho

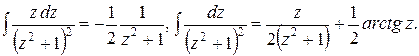
Таким образом,

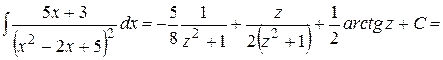
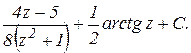
Возвращаясь к переменной 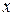, получаем

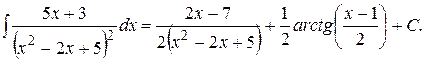
Итак, установлено, что интегрирование любой рациональной функции сводится к интегрированию многочлена и конечного числа элементарных дробей, интегралы от которых выражаются через рациональные функции, логарифмы и арктангенсы. Иными словам любая рациональная функция интегрируется в элементарных функциях.