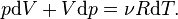Теплоёмкость идеального газа при постоянном давлении и при постоянном объёме.
В молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна:
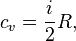
где R ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная.
А при постоянном давлении
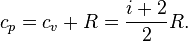
Переход вещества из одного агрегатного состояния в другое сопровождается скачкообразным изменением теплоёмкости в конкретной для каждого вещества температурной точке превращения — температура плавления (переход твёрдого тела в жидкость), температура кипения (переход жидкости в газ) и, соответственно, температуры обратных превращений: замерзания и конденсации.
Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К).
Уравнение Майера.
Для идеального газа справедливо Уравнение Майера:
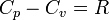 ,
,
где 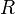 — универсальная газовая постоянная,
— универсальная газовая постоянная, 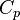 — молярная теплоёмкость при постоянном давлении,
— молярная теплоёмкость при постоянном давлении, 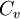 — молярная теплоёмкость при постоянном объёме.
— молярная теплоёмкость при постоянном объёме.
Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарному процессу в идеальном газе:
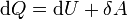 ,
,
в рассматриваемом случае:
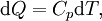
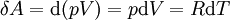 .
.
Уравнение Майера показывает, что различие теплоёмкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной 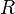 — механический эквивалент теплоты.
— механический эквивалент теплоты.
23)
Изохорный процесс:
При изохорном процессе объём не меняется и поэтому работа газа равна нулю. Изменение энергии согласно уравнению (Q=ΔU+A′) равно количеству переданной теплоты: ΔU=Q
Если газ нагревается, то Q>0 и ΔU>0, его внутренняя энергия увеличивается. При охлаждении газа Q<0 и ΔU= 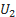 -
- 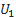 <0, изменение внутренней энергии отрицательно и внутренняя энергия газа уменьшается.
<0, изменение внутренней энергии отрицательно и внутренняя энергия газа уменьшается.
|
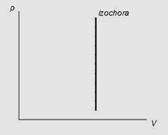
Термодинамика процесса:
Из определения работы следует, что изменение работы при изохорном процессе равно:
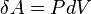
Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:
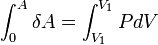 ,
,
Но такой интеграл равен нулю. Итак, при изохорном процессе газ работы не совершает:
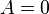 .
.
Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю.
Изменение внутренней энергии идеального газа можно найти по формуле:
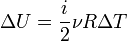 ,
,
где i — число степеней свободы, которое зависит от количества атомов в молекуле: 3 для одноатомной (неон), 5 для двухатомной (кислород) и 6 для трёхатомной и более (молекула водяного пара).
Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:
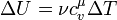 ,
,
где 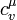 — молярная теплоёмкость при постоянном объёме.
— молярная теплоёмкость при постоянном объёме.
Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:
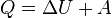
Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:
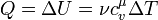 ,
,
то есть вся теплота, которую получает газ идёт на изменение его внутренней энергии.
Изобарный процесс:
При изобарном процессе согласно формуле (Q=ΔU+A′) передаваемое системе количество теплоты идет на изменение внутренней энергии системы и совершение работы при постоянном давлении (Согласно закону Гей-Люссака, при изобарном процессе в идеальном газе 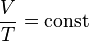 ).
).
|
Работа, совершаемая газом при расширении или сжатии газа, равна 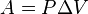 .
.
Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: 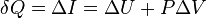 .
.
Если газ нагревается (Q>0), то он расширяется и совершает положительную работу (A′>0). Одновременно увеличивается его внутренняя энергия (ΔU>0).
При охлаждении (Q<0) газ сжимается и внешние силы совершают над ним положительную работу (А>0), его внутренняя энергия уменьшается (ΔU<0)
Изотермический процесс:
При изотермическом процессе (Т=const) внутренняя энергия идеального газа (U= 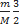 RT) не меняется. Согласно формуле (Q=ΔU+A′) все переданное системе количество теплоты идет на совершение работы:
RT) не меняется. Согласно формуле (Q=ΔU+A′) все переданное системе количество теплоты идет на совершение работы:
Q= A′
Если газ получает теплоту (Q>0), то он совершает положительную работу (A′>0).
Если газ отдаёт теплоту окружающей среде (термостату), то Q<0 и A′<0. Работа же внешних сил над газом в последнем случае положительна.
Работа, совершенная идеальным газом в изотермическом процессе, равна 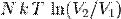 , где
, где 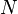 — число частиц газа,
— число частиц газа, 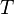 — температура,
— температура, 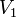 и
и 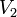 — объём газа в начале и конце процесса,
— объём газа в начале и конце процесса, 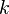 — постоянная Больцмана .
— постоянная Больцмана .
|
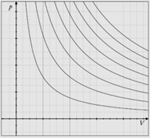
Адиабатический процесс
Адиабатный процесс-это процесс в теплоизолированной системе.
Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике.
Физический смысл адиабатического процесса:
Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена ( 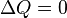 ) системы со средой сводится только к последним двум процессам[. Поэтому, первое начало термодинамики в этом случае приобретает вид
) системы со средой сводится только к последним двум процессам[. Поэтому, первое начало термодинамики в этом случае приобретает вид
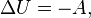
где 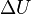 — изменение внутренней энергии тела,
— изменение внутренней энергии тела, 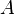 — работа, совершаемая системой.
— работа, совершаемая системой.
Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит:
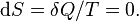
Здесь 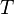 — температура системы,
— температура системы, 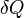 — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла
— теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла
Уравнение Пуассона
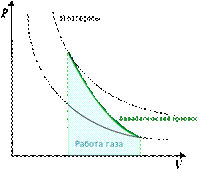
Адиабата Пуассона
Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением:
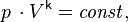
где 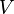 — его объём,
— его объём, 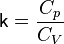 — показатель адиабаты,
— показатель адиабаты, 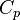 и
и 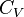 — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
— теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду
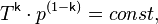
где 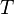 — абсолютная температура газа. Или к виду
— абсолютная температура газа. Или к виду
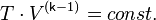
Поскольку  всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении
всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении 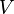 ) газ нагревается (
) газ нагревается ( 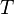 возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент
возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент  .
.
|
Вывод уравнения
Согласно закону Менделеева — Клапейрона для идеального газа справедливо соотношение
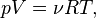
где R — универсальная газовая постоянная. Вычисляя полные дифференциалы от обеих частей уравнения, полагая независимыми термодинамическими переменными 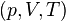 , получаем
, получаем
|
Если в (3) подставить 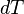 из (2), а затем
из (2), а затем 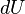 из (1), получим
из (1), получим
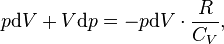
или, введя коэффициент 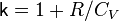 :
:
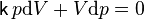 .
.
Это уравнение можно переписать в виде
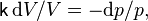
что после интегрирования даёт:
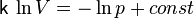 .
.
Потенцируя, получаем окончательно:
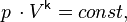 что и является уравнением адиабатического процесса для идеального газа.
что и является уравнением адиабатического процесса для идеального газа.

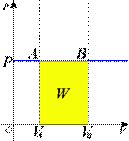
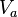 до
до 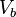 . AB здесь является изобарой.
. AB здесь является изобарой. 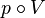 диаграмме для газа.
диаграмме для газа. 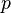 — давление газа;
— давление газа;