Отражение и преломление плоских электромагнитных волн

Теоретические сведения

Отражение и преломление плоских ЭМВ. Под отражением понимают процесс взаимодействия электромагнитных волн с телами, находящимися на пути их распространения, при котором структура результирующего поля может быть представлена в виде конечной суперпозиции волн той же самой структуры. Наиболее простые результаты получаются при рассмотрении отражения плоских волн. Электромагнитная волна может рассматриваться как плоская только в ограниченном объеме, линейные размеры которого много меньше расстояния от него до источника электромагнитных волн.

При падении плоской волны на границу раздела двух сред выделяют плоскость падения (плоскость XOZ на рис. 5.1), содержащую векторы Пойнтинга в падающей, отраженной и преломленной волнах. Если векторы 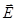в этих волнах параллельны плоскости падения, то поляризацию волн называют параллельной (рис. 5.1), а если векторы 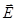перпендикулярны плоскости падения, то говорят о перпендикулярной поляризации (рис. 5.2). 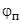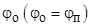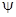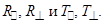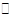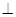Для описания процесса отражения и преломления вводят угол падения , угол отражения , угол преломления и коэффициенты отражения и преломления по электрическому полю Индексы и обозначают соответствующий тип поляризации.

Предполагают, что среды являются однородными изотропными линейными, для которых справедливы граничные условия (материальные отношения).

Рассмотрим отражение плоской линейно-поляризованной волны, вектор E которой лежит в плоскости падения, от плоской границы раздела двух сред. Если источники электромагнитного поля находятся в первой среде, то, очевидно, поле в первой среде будет суперпозицией падающей и отраженной волн, а поле во второй среде будет существовать только в виде одной волны (преломленная волна). Вводя координаты, как показано на рис. 5.1, указанные волны можно представить в виде:

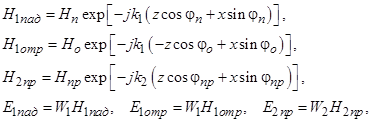
где 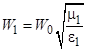, , 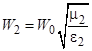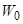– волновое сопротивление свободного пространства, 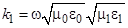, 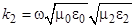– волновые числа первой и второй среды.

Законы Снеллиуса:

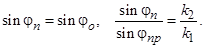
Для вектора напряженности магнитного поля можно записать выражение 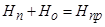, так как эти векторы параллельны друг другу.

Формулы Френеля для параллельной поляризации:

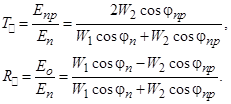
Для идеальных диэлектриков эти уравнения можно переписать в следующем виде:

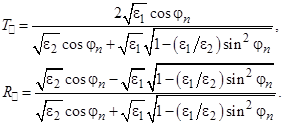
Формулы Френеля для перпендикулярной поляризации: (вектор падающей волны перпендикулярен плоскости падения, рис. 2).

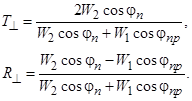
Поскольку любую плоскую электромагнитную волну можно представить в виде суммы волнс параллельной и перпендикулярной поляризациями, то можно, используя формулы Френеля, найти электромагнитные поля в произвольном случае отражения.

Полное прохождение. При выполнении условия 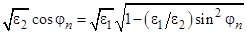величина , и, следовательно, отраженная волна в первой среде будет отсутствовать. Угол падения, при котором наблюдается такое явление, называется углом Брюстера.

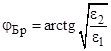
Угол Брюстера можно найти для любого соотношения между ε₁ и ε₂. Для перпендикулярной поляризации угол полного прохождения между разнородными диэлектриками ( 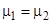) не существует, 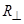всегда больше 0. Угол Брюстера называют также углом полной поляризации. Плоские волны круговой и эллиптической поляризации можно представить в виде суперпозиции двух линейно поляризованных плоских волн, одна из которых (поляризована нормально, а другая – параллельно плоскости падения. Так как условия существования угла Брюстера для параллельной и нормальной поляризации различны, то волны с круговой и эллиптической поляризациями будут отражаться при любых углах падения ( 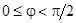). Однако при этом соотношение между амплитудами нормальной и параллельной составляющих в отраженной и преломленной волнах будет иным, чем в падающей волне. Это приводит к изменению (поляризации отраженной и преломленной волн по сравнению с падающей. В частности, если плоская волна с круговой поляризацией падает под углом Брюстера для одной из двух образующих ее линейно поляризованных волн, то отраженная волна оказывается линейно поляризованной, а преломленная – эллиптически поляризованной.

Полное внутреннее отражение. Определим условия, при которых отсутствует преломленная волна, т. е. имеет место полное отражение. Угол преломления 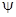может изменяться от нуля до π/2. Значение 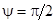является предельным. Назовем угол падения 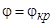, при котором 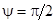, критическим углом. Полагая во втором законе Снеллиуса 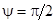, получаем 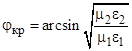. Так как 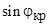не может быть больше единицы, полученное равенство возможно лишь в том случае, если 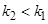, т. е. при условии, что вторая среда является оптически менее плотной, чем первая.

При углах падения, больших критического имеет место полное отражение, т. е. по абсолютной величине коэффициент отражения должен быть равен единице.

Для возникновения полного отражения необходимо выполнение двух условий:

– вторая среда должна быть оптически менее плотной по сравнению с первой ();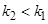

– угол падения должен быть больше критического ( ).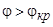

Запишем выражения для коэффициентов отражения и преломления при углах падения больше критического:

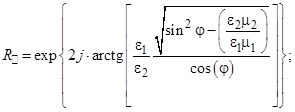
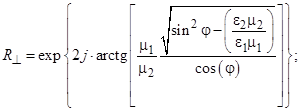
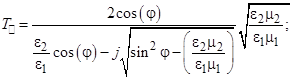
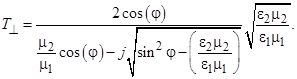
Из полученных выражений следует, что поле в первой среде имеет структуру плоской волны, распространяющейся вдоль поверхности раздела.

Во второй среде образовалась волна с плоским фазовым фронтом, перпендикулярным оси x, и меняющейся вдоль этого фронта амплитудой – плоская неоднородная волна. Неоднородная волна с экспоненциально убывающей амплитудой при удалении от граничной поверхности (как бы прилипающая к этой поверхности) называется поверхностной. Фазовая скорость и длина волны такие же, как в первой среде.

Экспоненциальное убывание амплитуды волны в направлении z определяется коэффициентом a, зависит от угла падения j и не связано с потерями во второй среде (они здесь не учитываются). Более детальные исследования показывают, что волна в среде 2 движется по эллиптическим траекториям, проходя определенное расстояние вдоль оси z.

Падение ЭМВ на границу поглощающей среды. Пусть плоская волна падает под углом 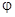на плоскую границу раздела двух сред, из которых первая – идеальный диэлектрик, а вторая – поглощающая. В этом случае можно использовать формулы Френеля, если считать 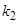комплексной величиной: .

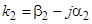Относительная диэлектрическая проницаемость среды с потерями может быть выражена формулой:

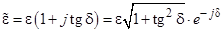
где 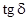– тангенс угла диэлектрических потерь.

Волновое сопротивление среды с потерями .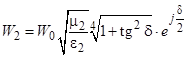

Параметр 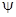нельзя рассматривать как геометрический угол. Введем обозначения:

.

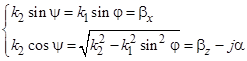Запишем поле во второй среде, ограничиваясь случаем нормальной поляризации:

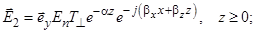
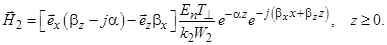
Поле в поглощающей среде представляет собой плоскую волну, волна является неоднородной: поверхности равных фаз не совпадают с поверхностями равных амплитуд. Направление распространения волны образует некоторый угол с осью z, называемый действительным углом преломления :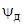

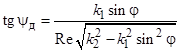
Амплитуды векторов E и H экспоненциально убывают в направлении нормали к поверхности раздела (вдоль оси Z). Имеется продольная по отношению к направлению распространения преломленной волны составляющая вектора Н (в случае нормальной поляризации) или продольная составляющая вектора Е (в случае параллельной поляризации).

Поле в первой среде складывается из падающей и отраженной волн и не имеет принципиальных особенностей по сравнению с полем, возникающим при отражении волны от границы раздела двух диэлектриков.

Аналогичные результаты можно получить, анализируя случай параллельной поляризации.

Практически важным является случай, когда вторая среда оптически намного плотнее первой. Частным случаем таких сред являются хорошо проводящие среды (металлы). У металлов 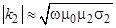. Так как удельная проводимость 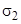велика, то .

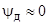Это означает, что при любом угле падения φ на поверхность хорошо проводящей среды преломленная волна распространяется практически вдоль нормали к поверхности раздела. Плоскости равных фаз и плоскости равных амплитуд при этом (практически совпадают, и волну можно считать однородной. Продольная по отношению к направлению распространения составляющая вектора Н (или, в случае параллельной поляризации, вектора Е) будет пренебрежимо мала по сравнению с поперечной составляющей. Можно считать, таким образом, что волна является поперечной, причем векторы Е и Н в ней сдвинуты по фазе друг относительно друга на угол .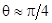

Поле во второй среде для нормальной поляризации может быть описано следующими формулами:

,

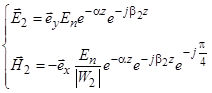где .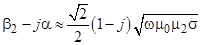

Подчеркнем, что амплитуды векторов Е и Н преломленной волны в металле быстро убывают с удалением от границы раздела и волна фактически существует лишь в тонком слое вблизи поверхности раздела. Глубина проникновения поля в проводник 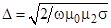.