Главное значение (в смысле Коши)

Если функция такова, что при любом существуют собственные интегралы

и ,

то под главным значением в смысле Коши (v. p.) понимается число

v. p. .

24. признаки сравнения несобственных интегралов от неотрицательных функций. Следствие.

Все теоремы сформулированы для положительных функций, однако они справедливы для знакопостоянных функций.

Теоремы сравнения.

А) Несобственные интегралы с бесконечными пределами интегрирования

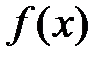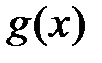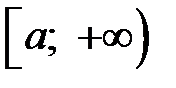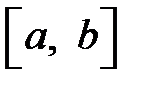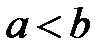Первая теорема сравнения. Пусть и определены на , интегрируемы на любом отрезке , где и 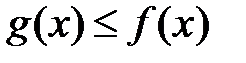, причем 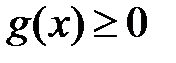. Тогда:

1. если сходится 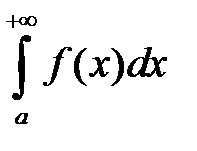, то сходится и ;

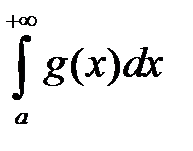2. если расходится 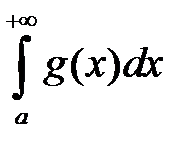, то расходится и .

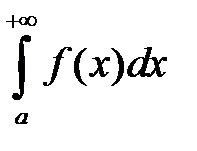Вторая теорема сравнения.Пусть функци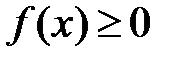и и 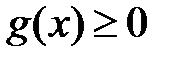определены на 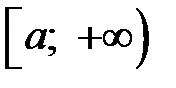, и пусть существует 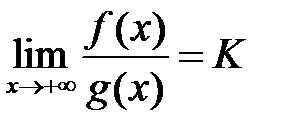. Тогда

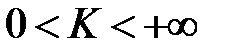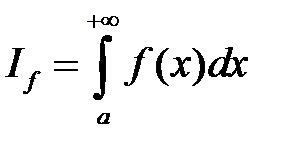1) Если , то и 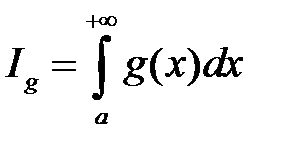сходятся или расходятся одновременно.

2) Если 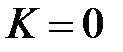, то из сходимости 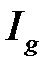следует сходимость 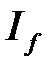, а из расходимости 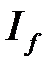следует расходимость .

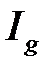3) Если 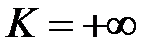, то из сходимости 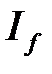следует сходимость 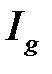, а из расходимости 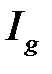следует расходимость .

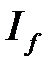Б) Несобственные интегралы от неограниченных функций.

Первая теорема сравнения. Пусть на отрезке 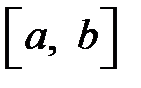функци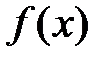и и 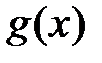разрывны в точке 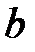, и для каждого 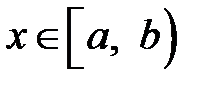выполняется неравенство 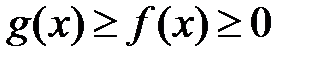. Тогда если сходится 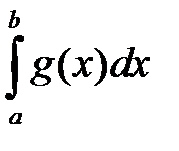, то сходится и 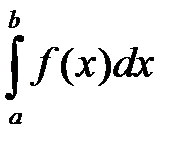; если расходится 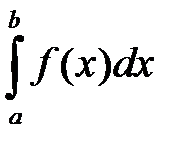, то расходится и .

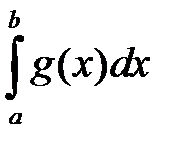Вторая теорема сравнения.Пусть на отрезке 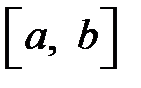функци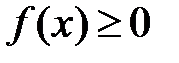и и 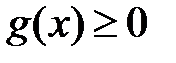разрывны в точке 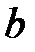, и пусть существует 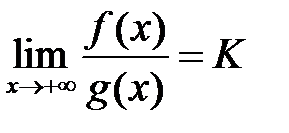. Тогда:

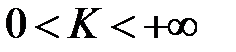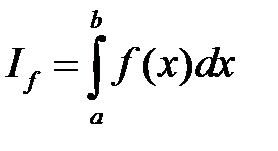1) Если , то и 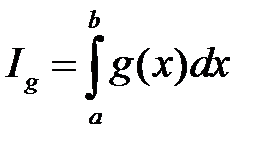сходятся или расходятся одновременно.

2) Если 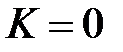, то из сходимости 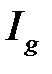следует сходимость 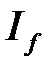, а из расходимости 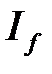следует расходимость .

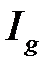3) Если 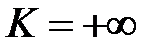, то из сходимости 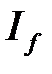следует сходимость 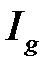, а из расходимости 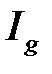следует расходимость .

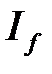25. Собственные интегралы зависящие от параметра, их непрерывности и дифференцируемости.

Для того чтобы дать определение интеграла, зависящего от параметра, введем функцию 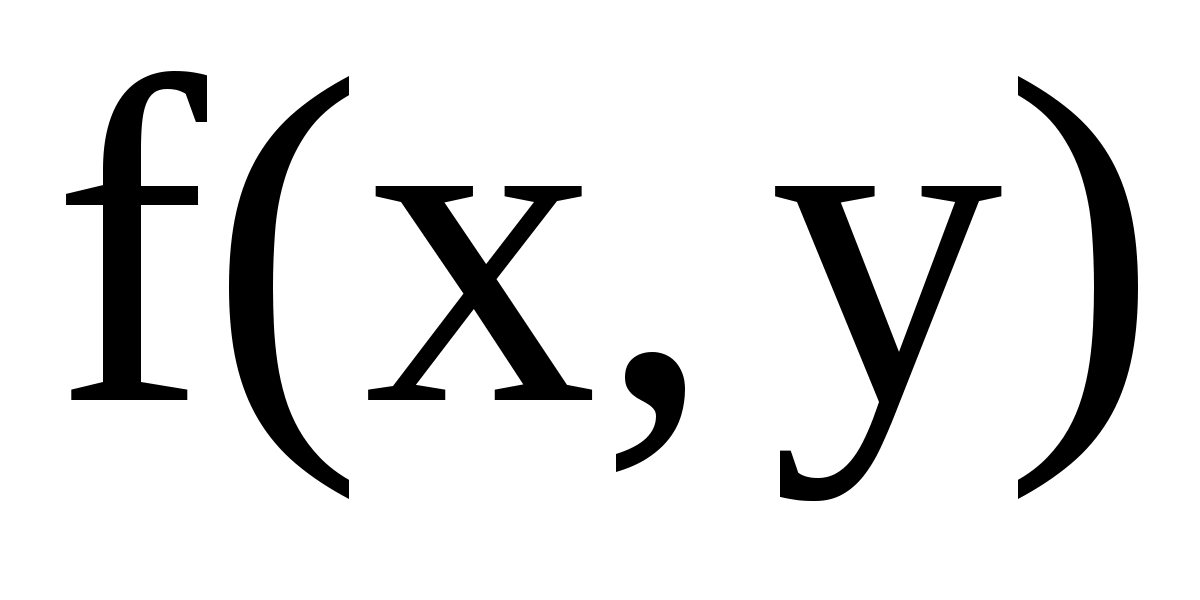. Пусть эта функция 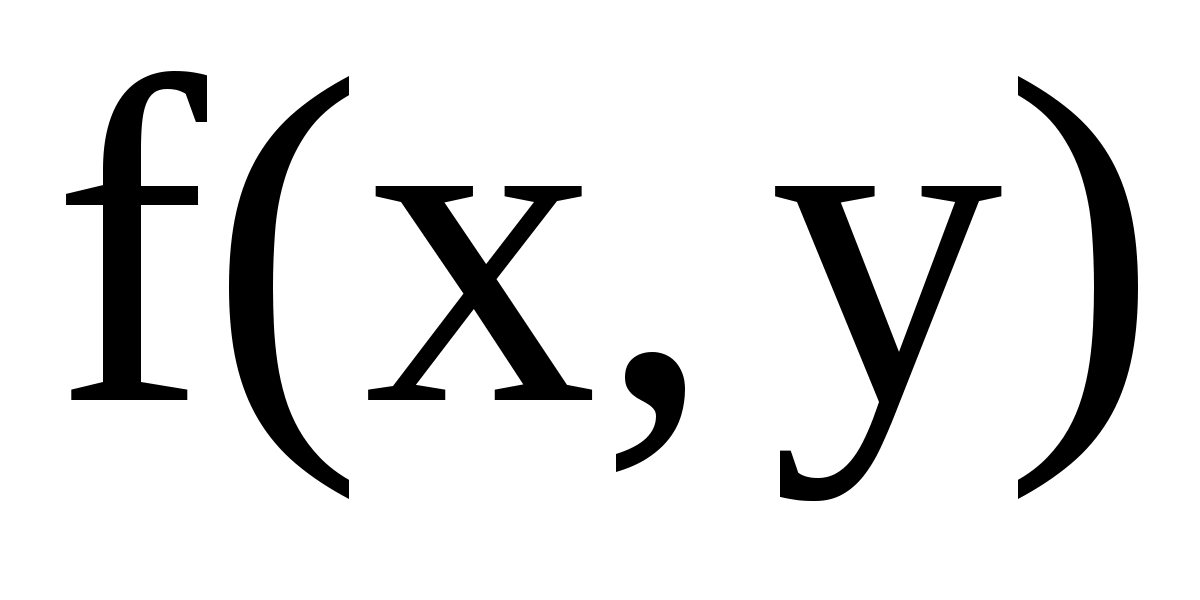будет определена на некотором множестве, где 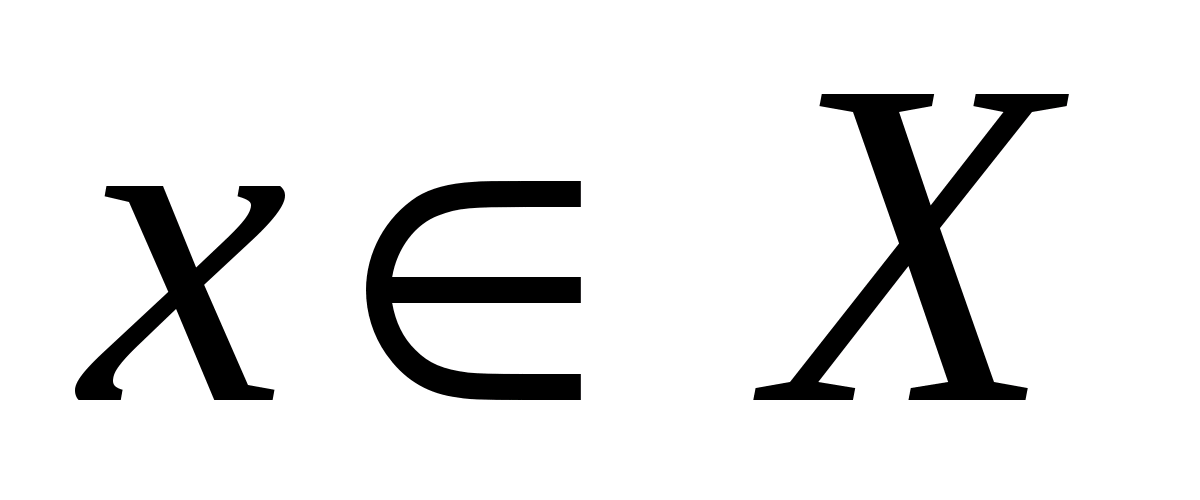и 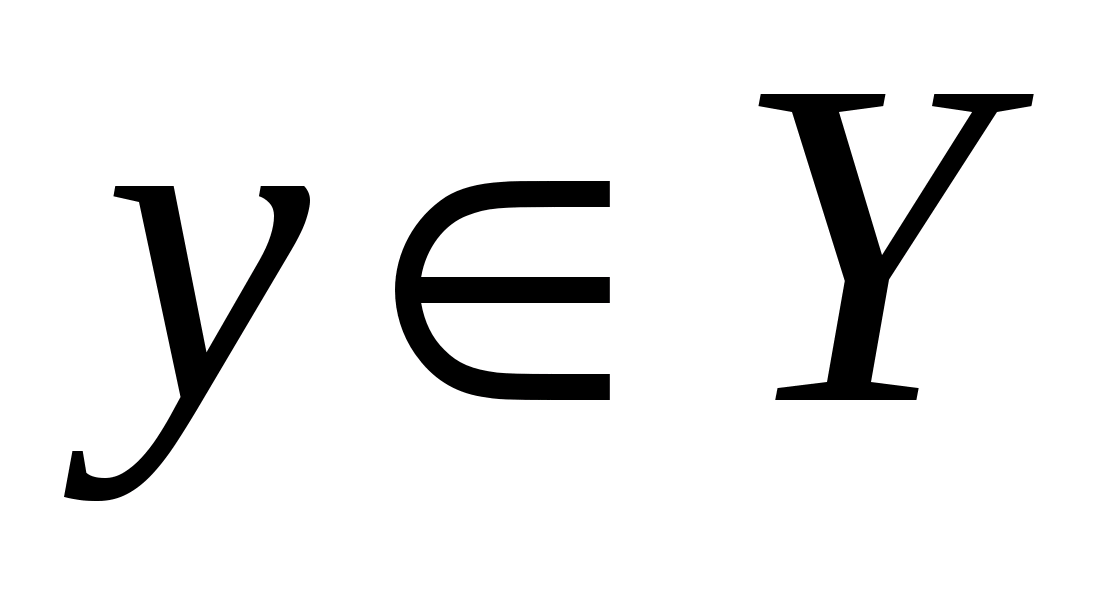, то есть в результате получится множество 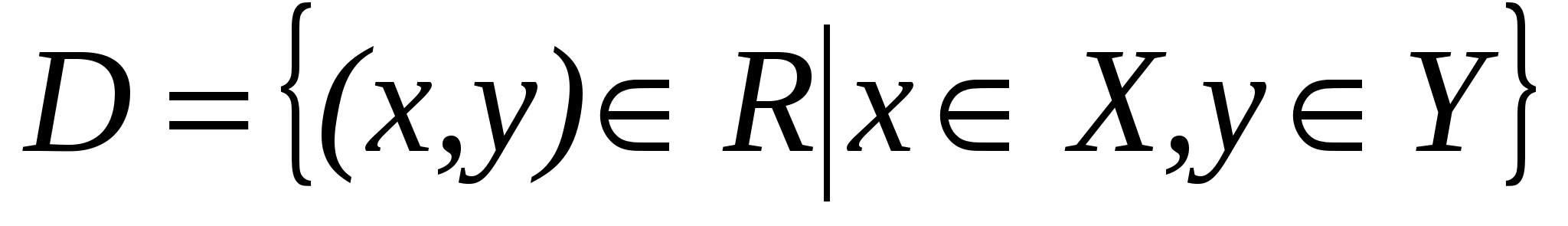. Если функция 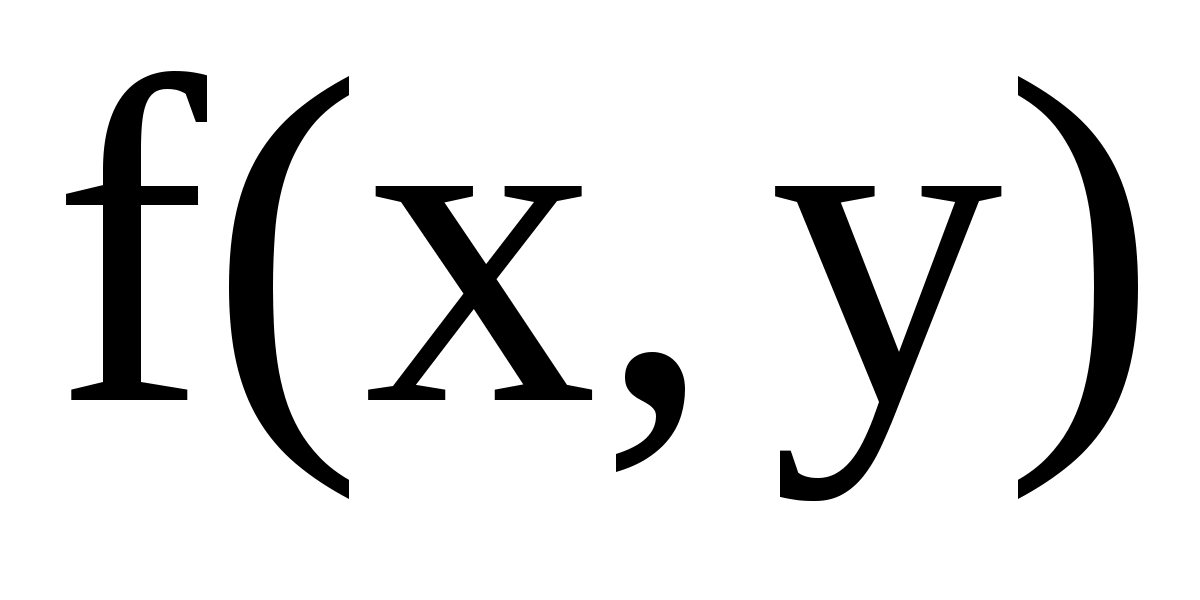непрерывна в D, то тогда имеет смысл интеграл 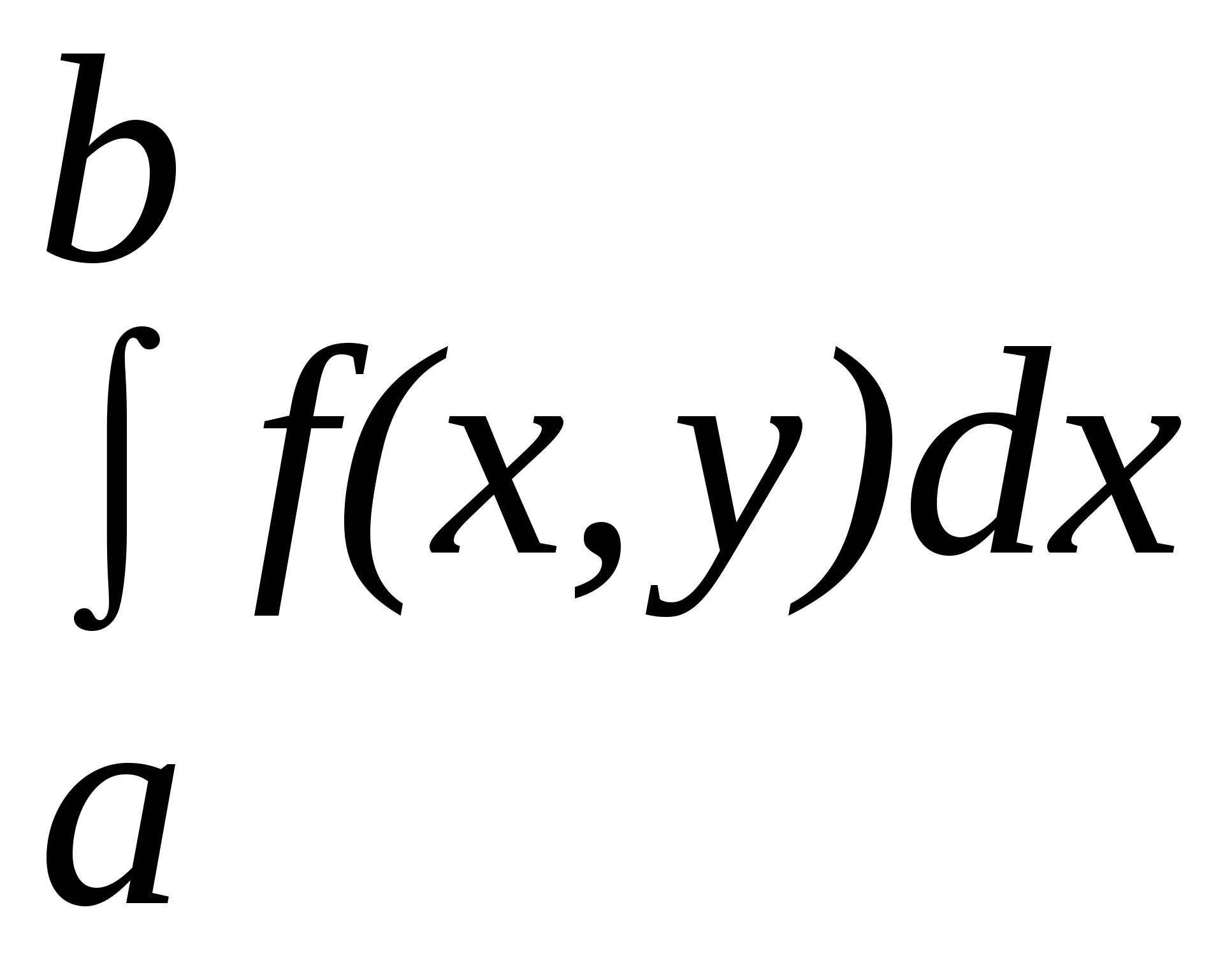, где x принадлежит некоторому конечному или бесконечному промежутку 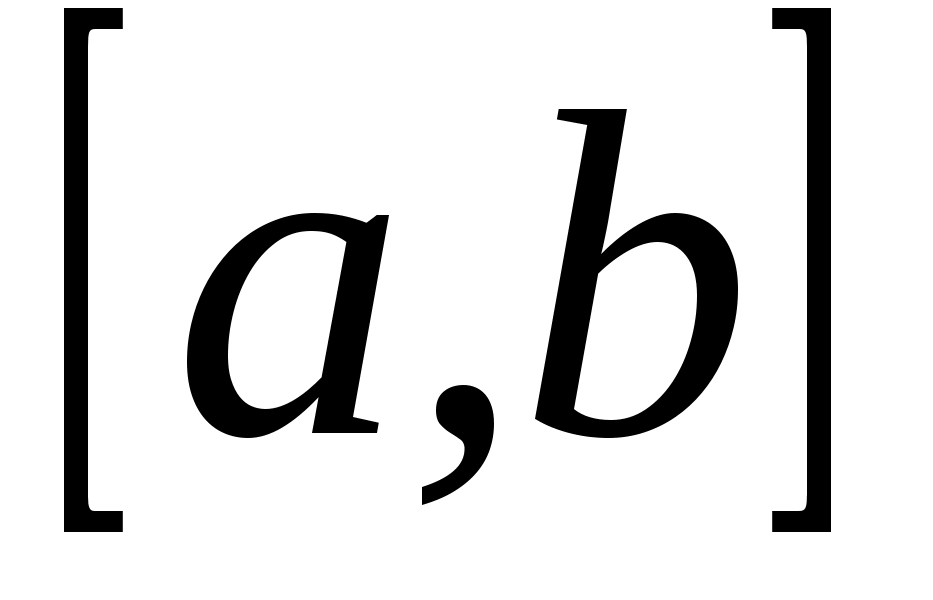, значит, интеграл может быть несобственным.

На основании этого можно дать определение интеграла, зависящего от параметра.

Определение.

Интеграл 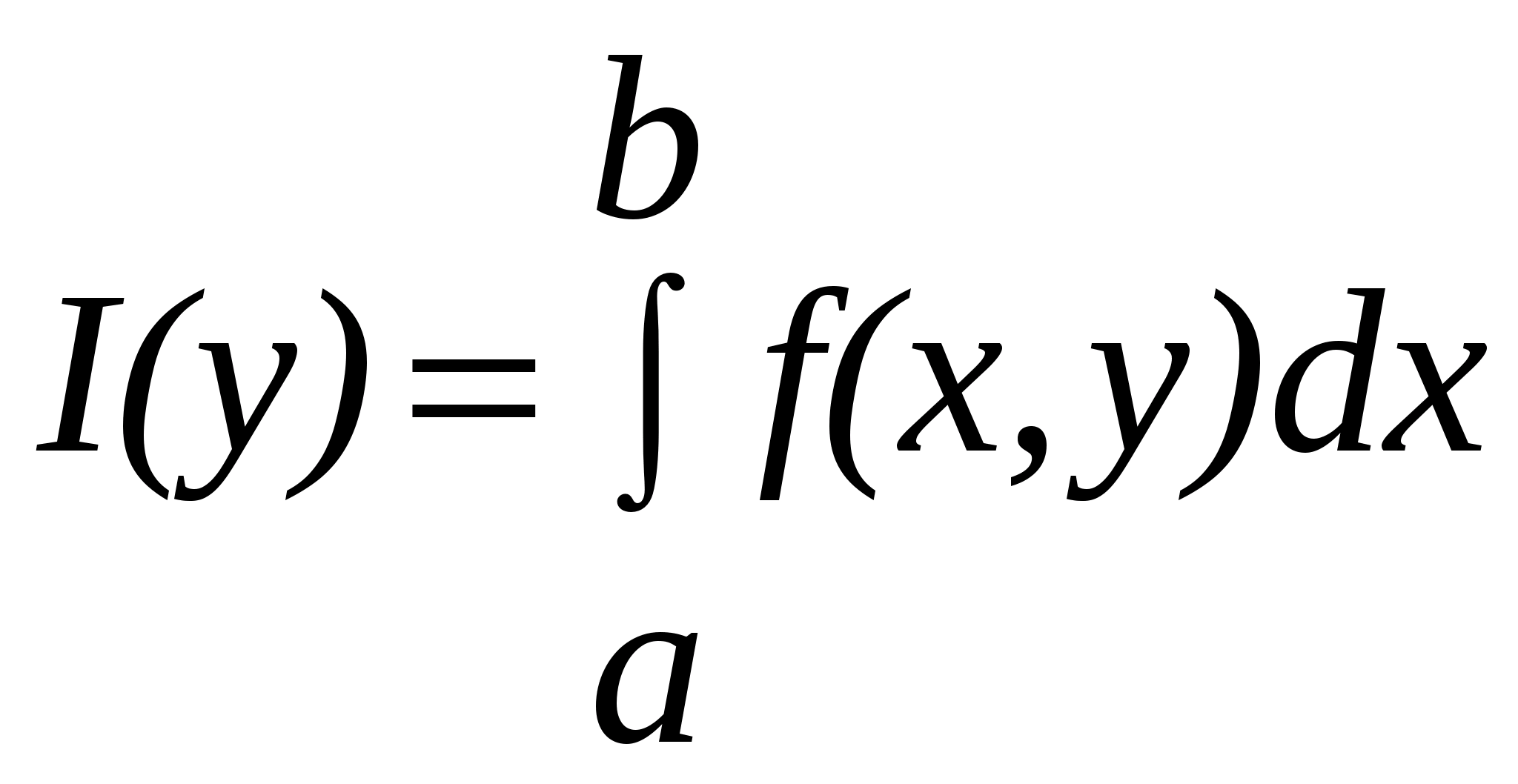называется интегралом, зависящим от параметра, если 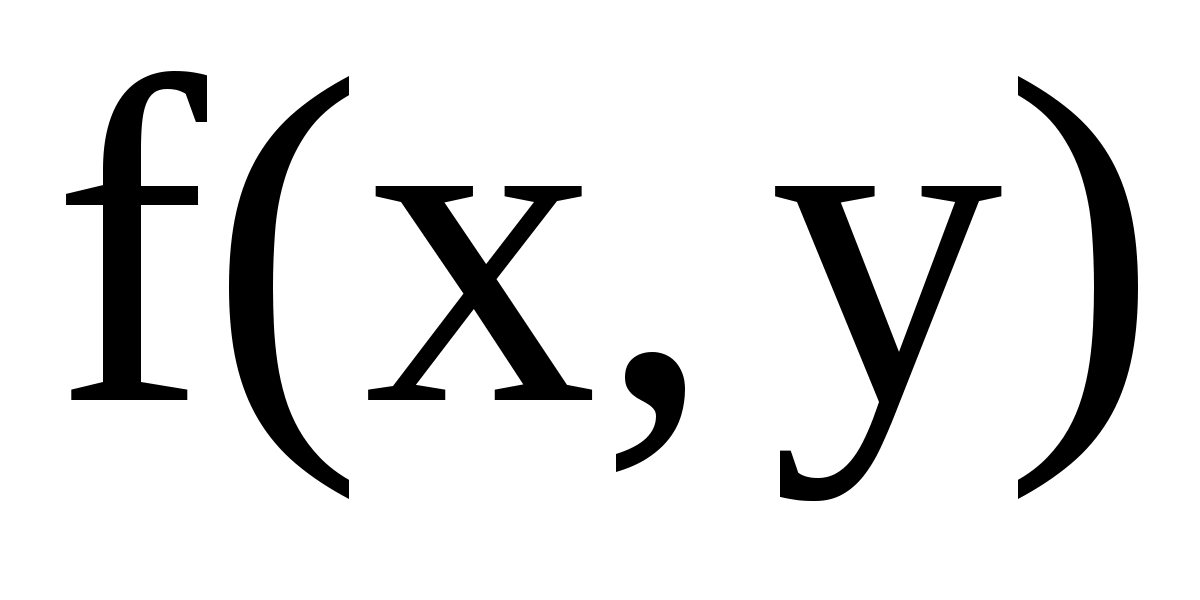интегрируема на промежутке 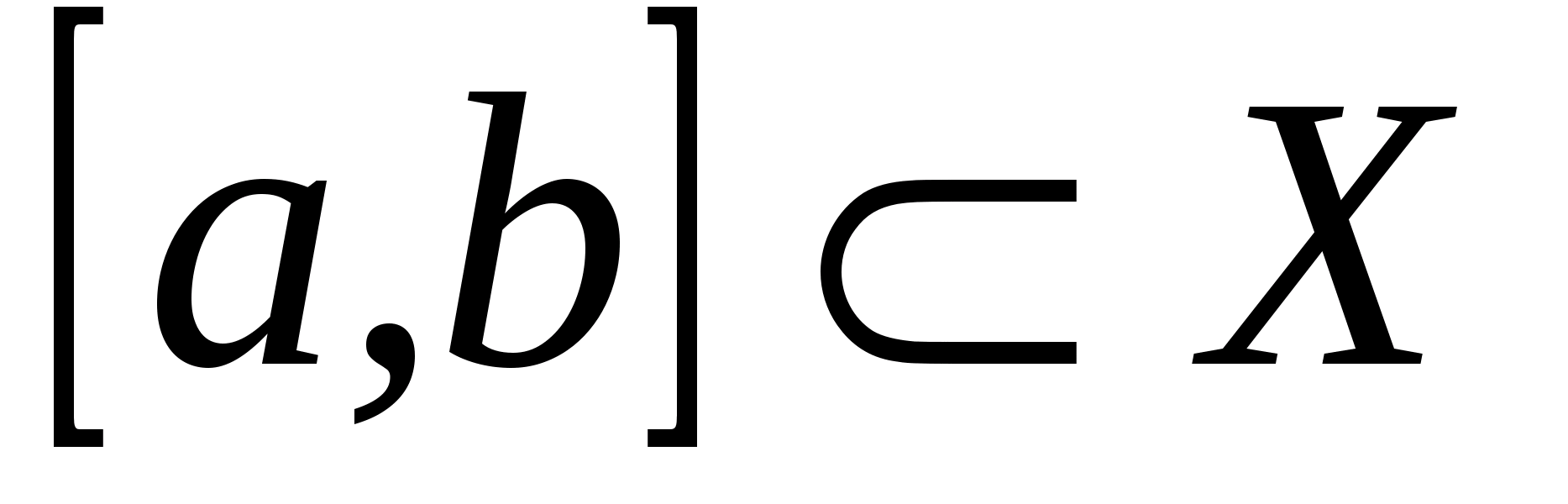при любом фиксированным 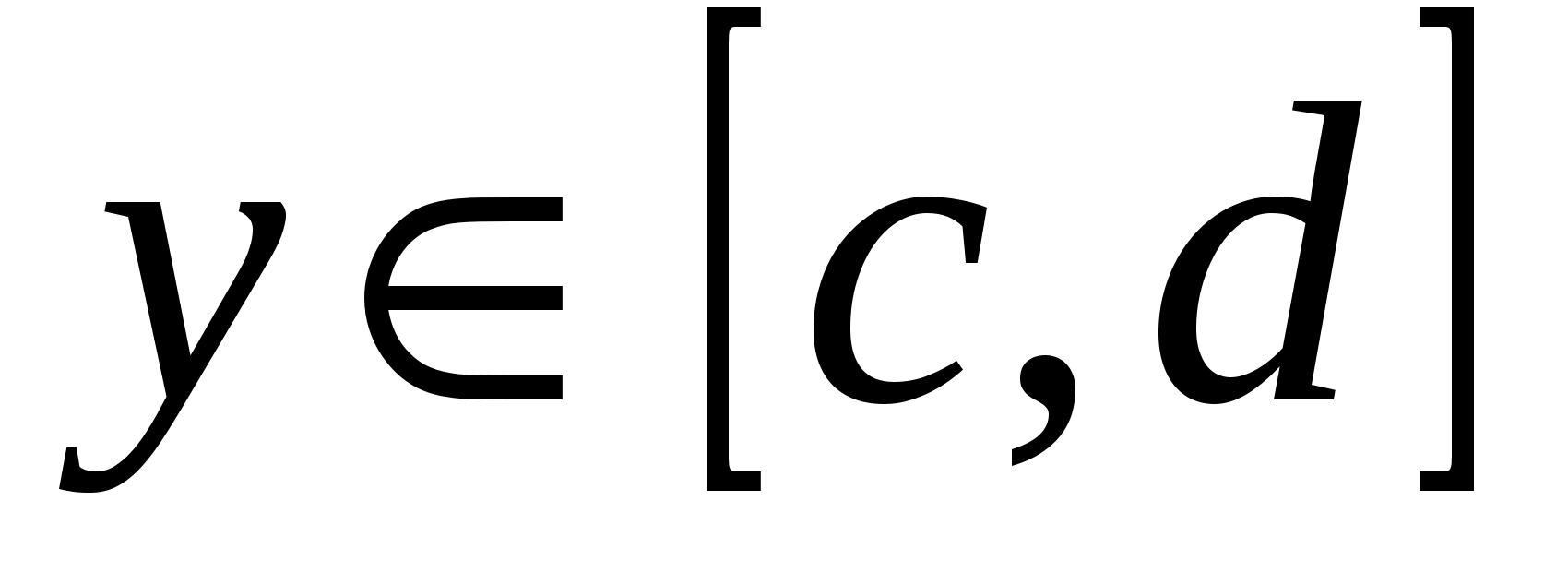, где .

Следовательно, представляет собой функцию 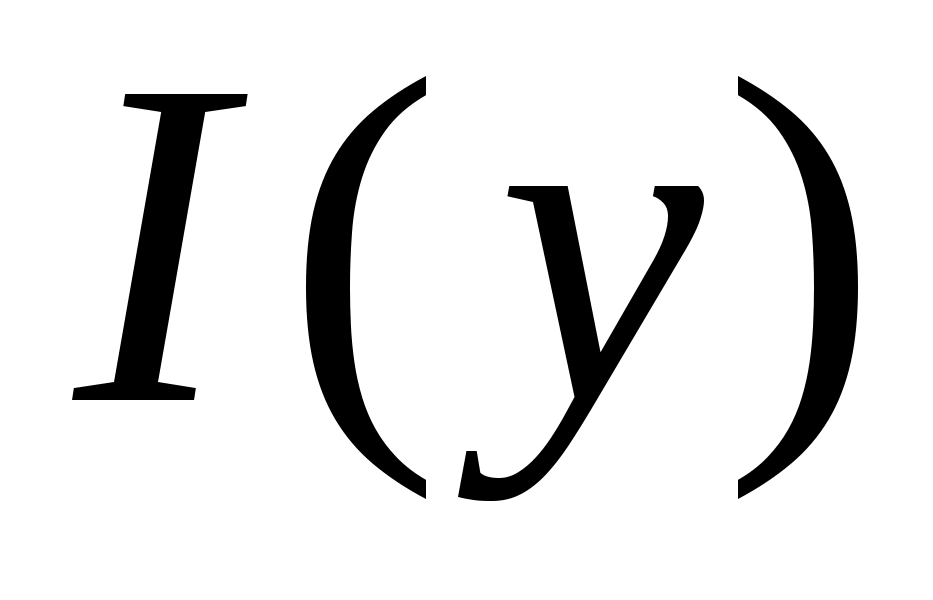переменной (параметра) 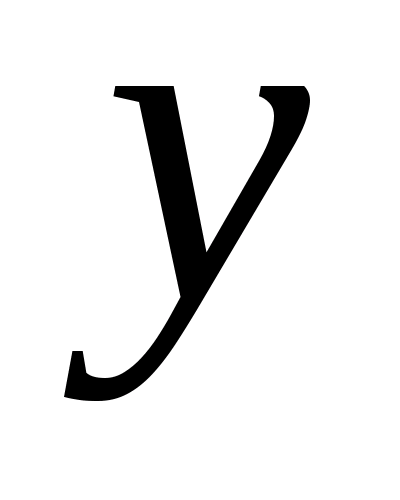, определенную в промежутке 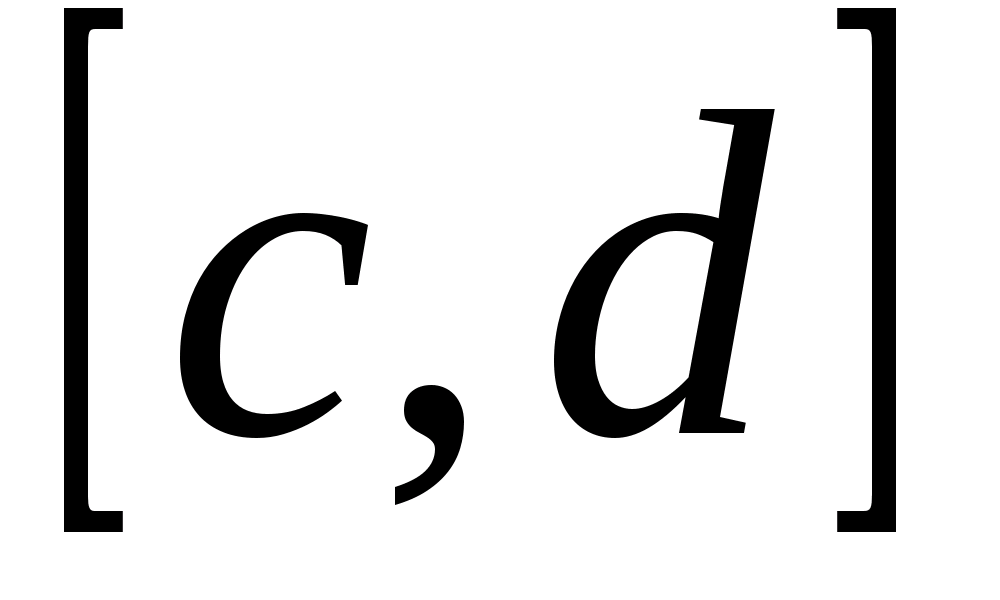. Возможно также существование интеграла при фиксированном 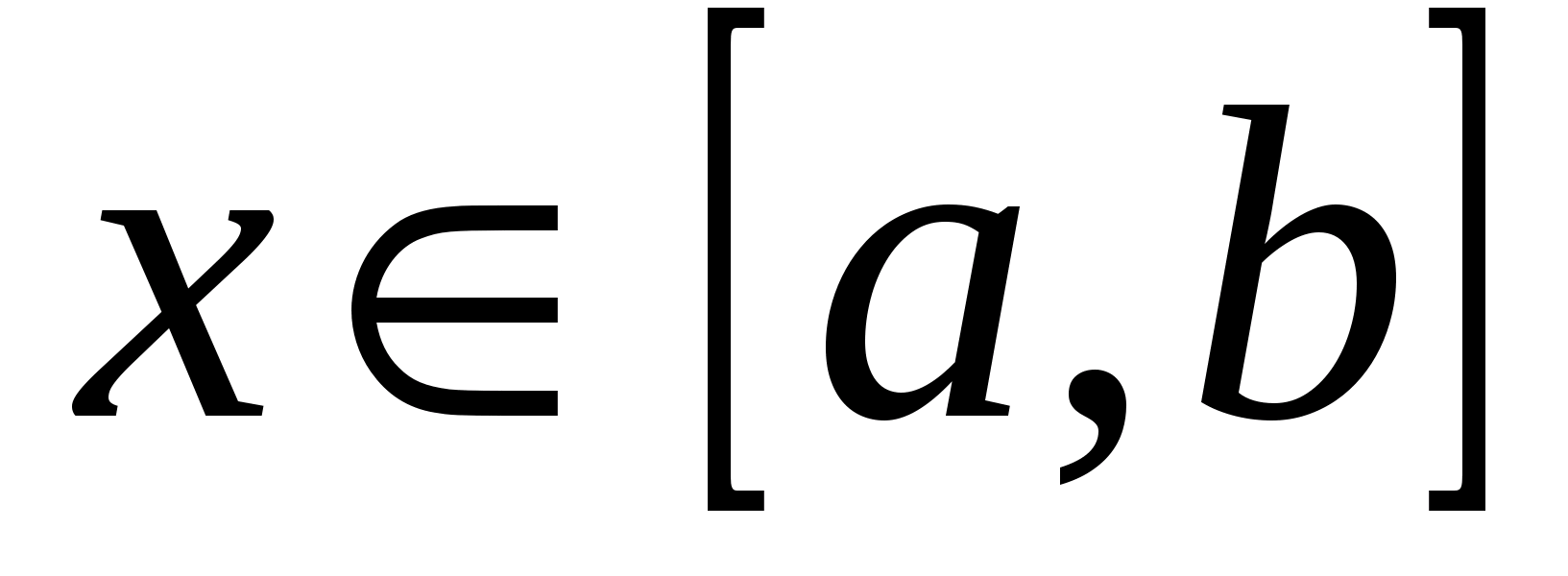, тогда он будет представлять собой функцию переменной (параметра) 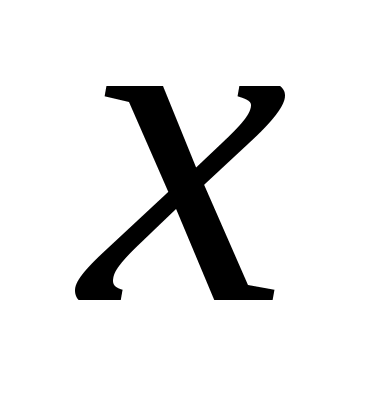, определенную в промежутке 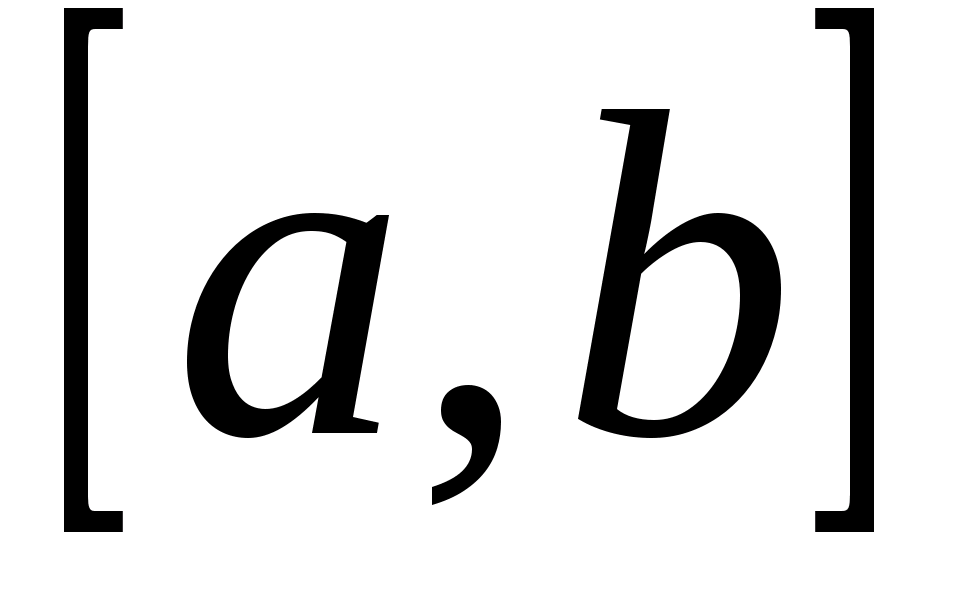. Обозначается она так 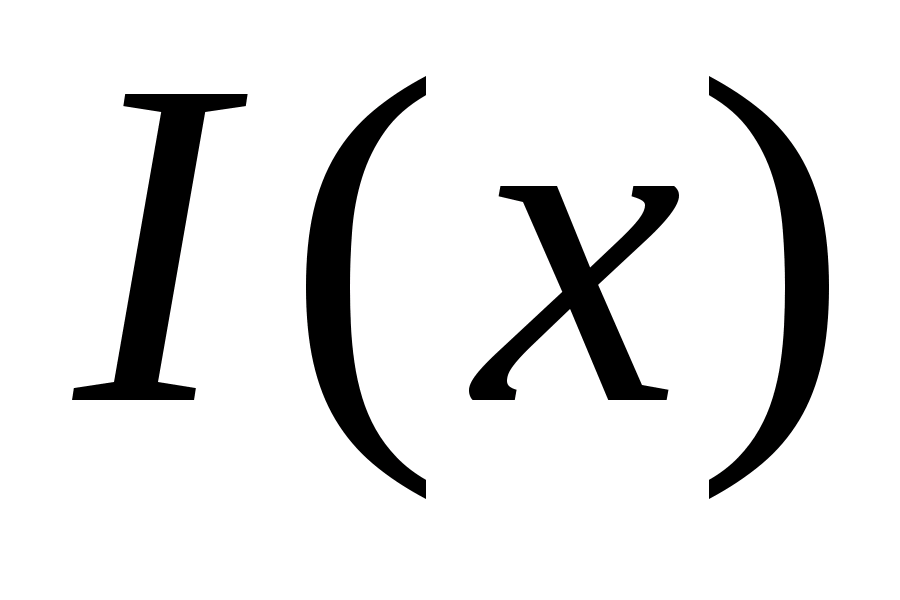, так что .

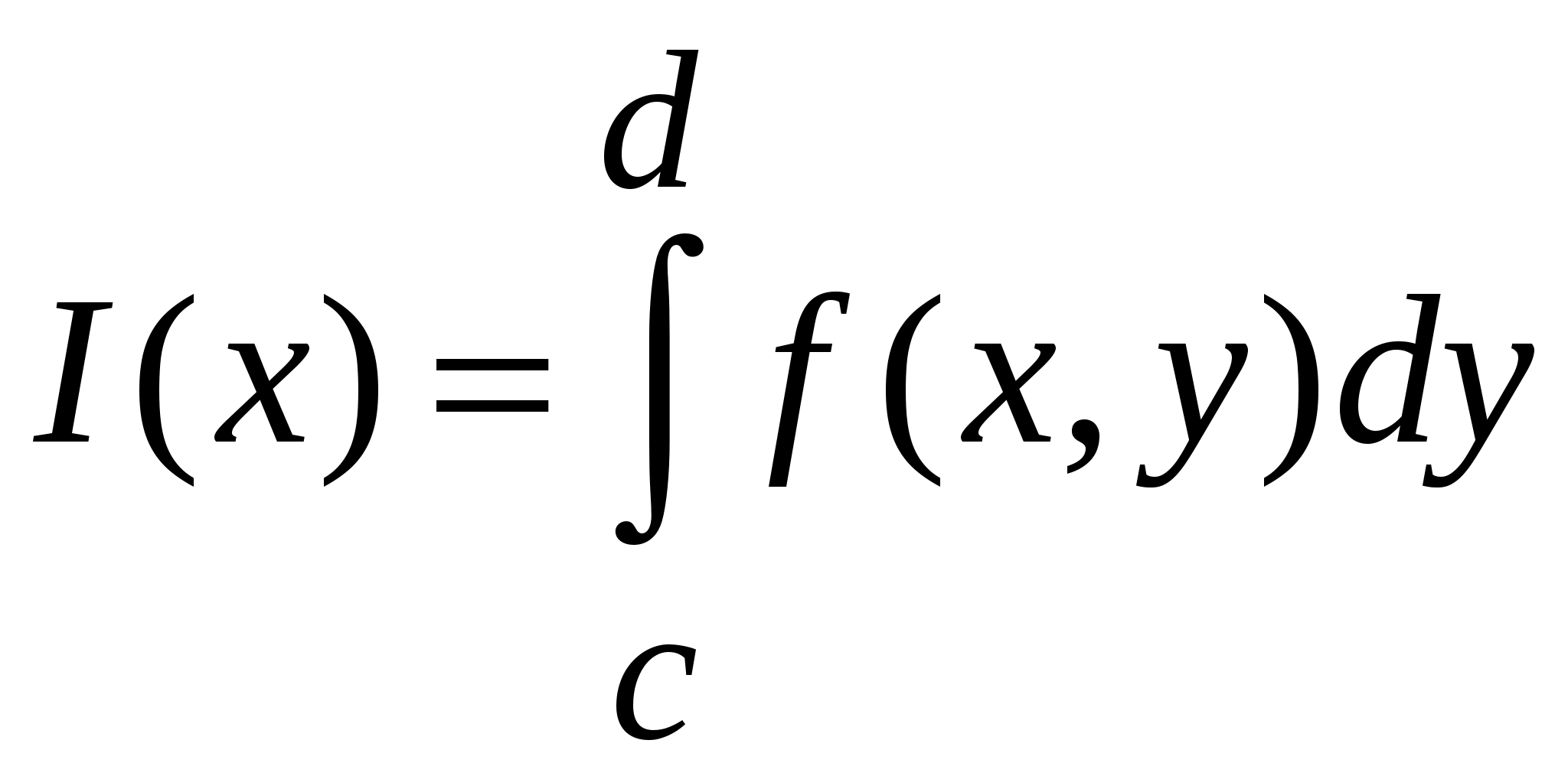Основная задача будет состоять в том, чтобы, зная свойства функции 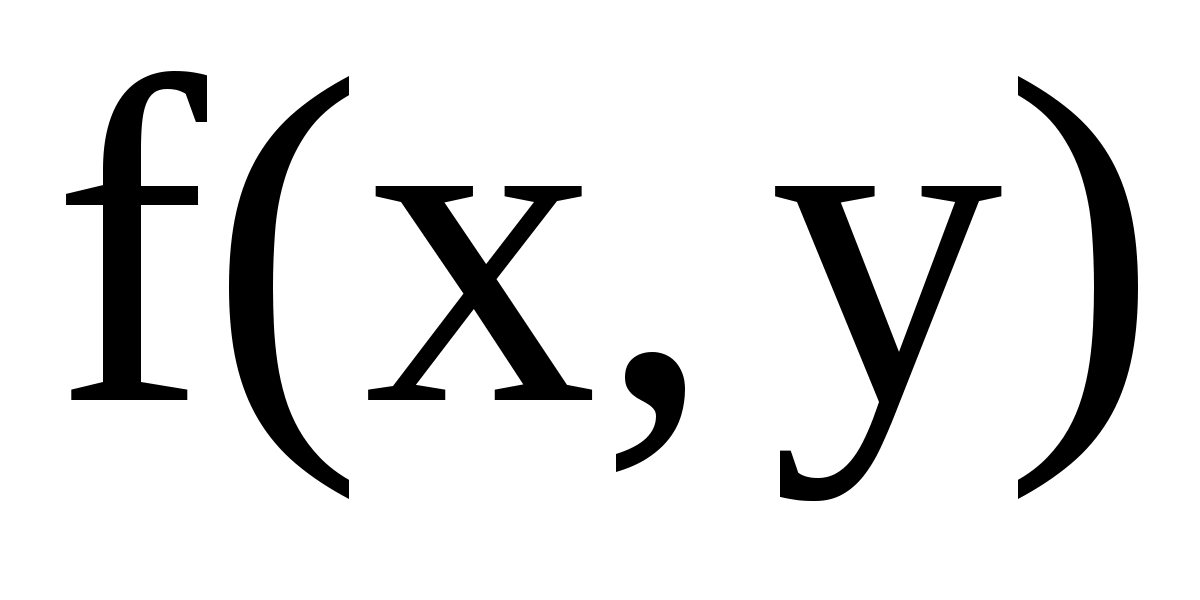, получить информацию о свойствах функции 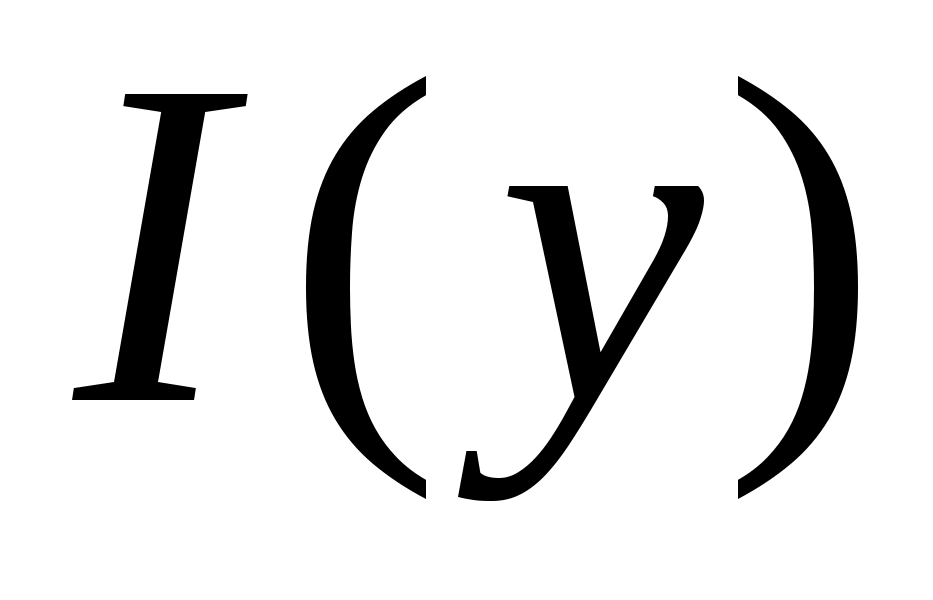. Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов.

Пример. Найти интеграл 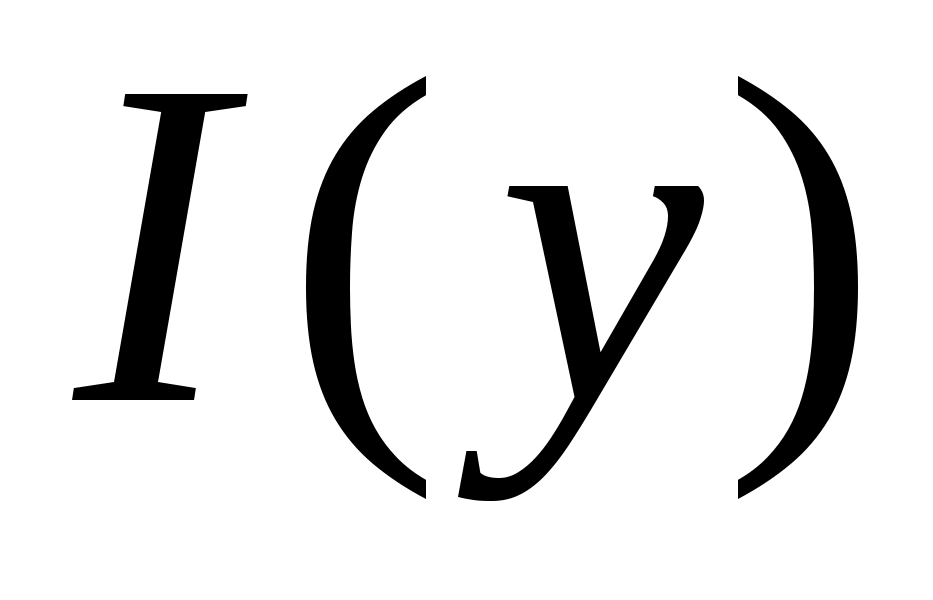от функции ,

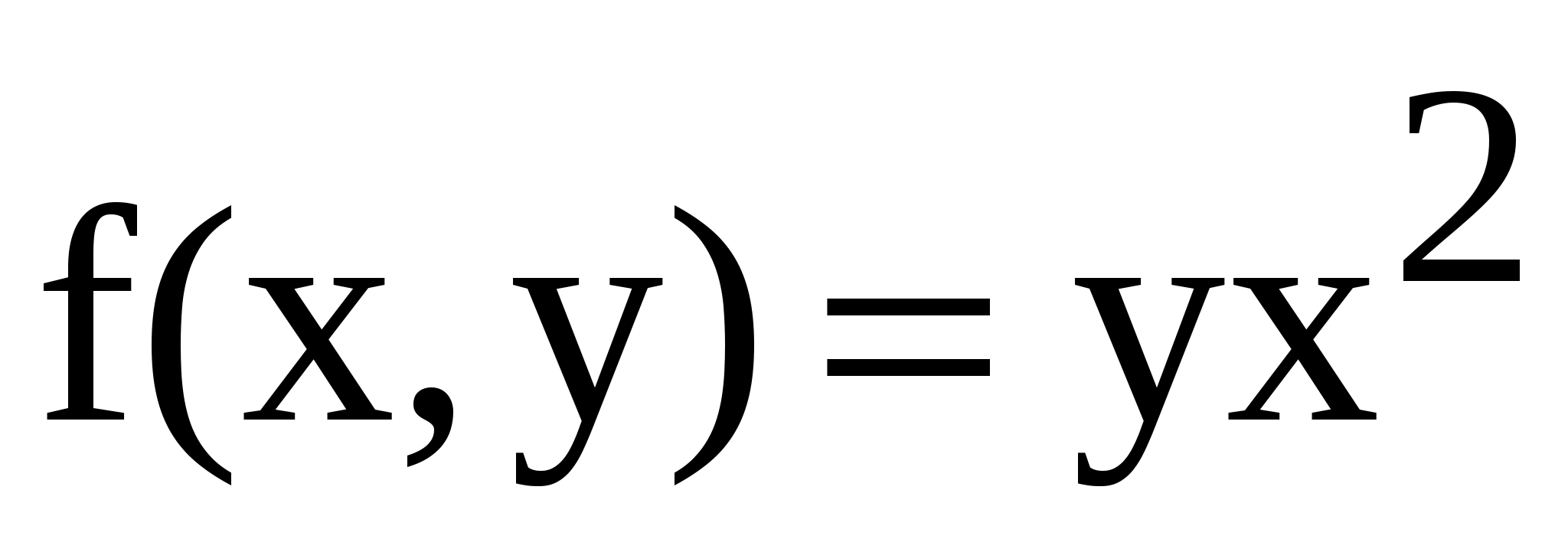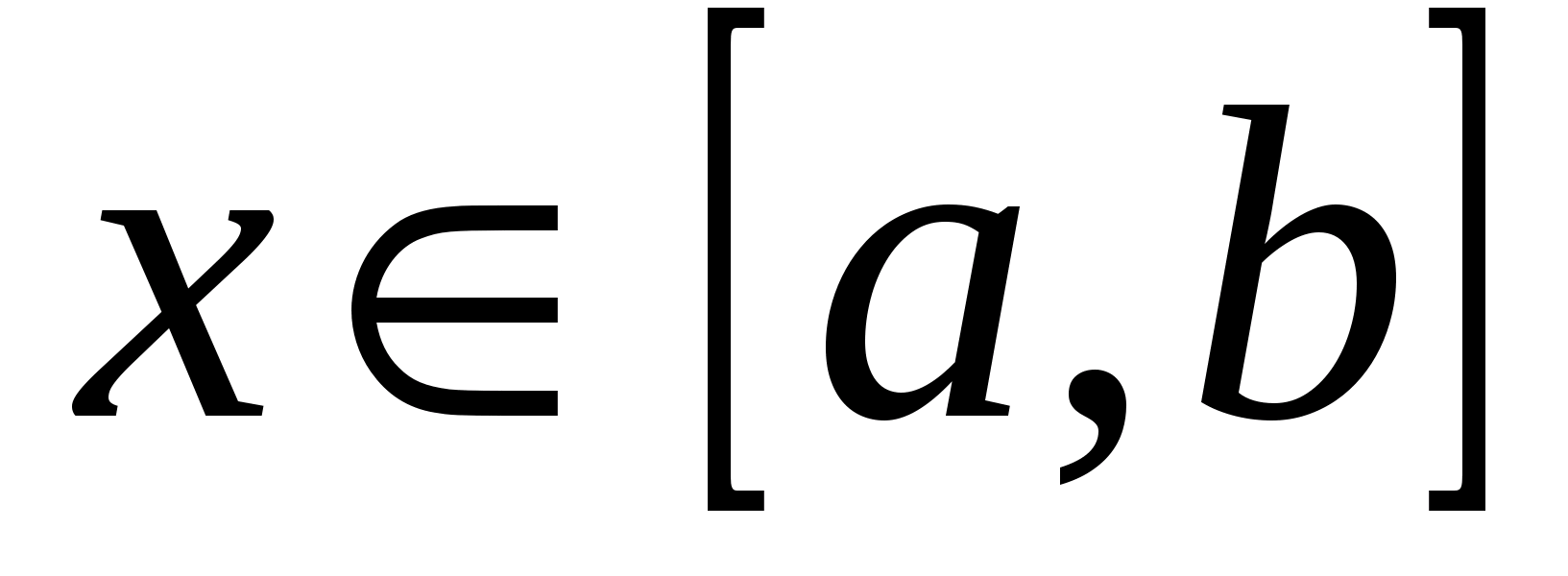
Функция 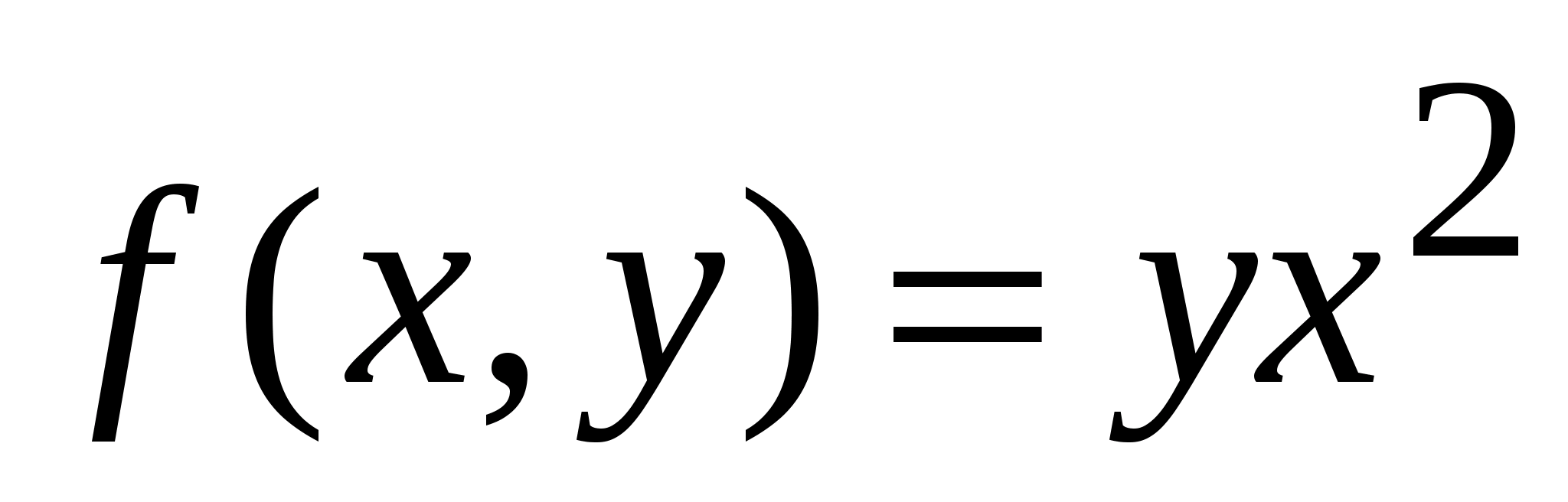непрерывна на отрезке 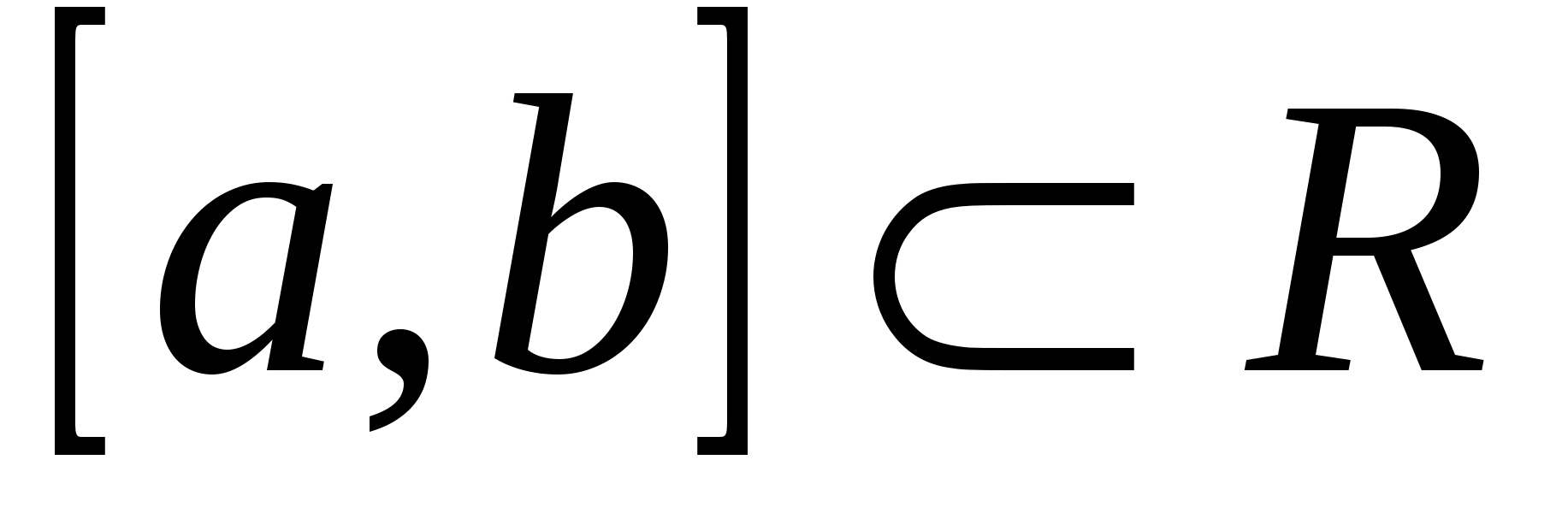при любом фиксированном 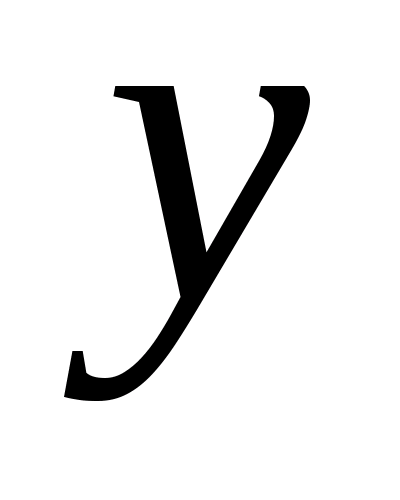, а значит, она интегрируема. Тогда

.
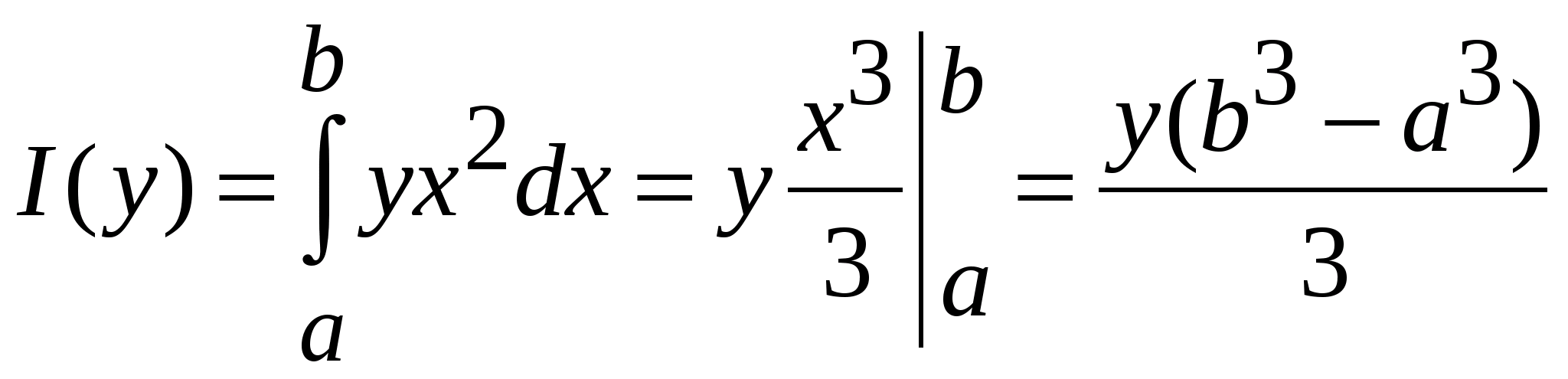