Дисконтирование по сложной ставке

1) Математическое дисконтирование– определение современной стоимости PV по будущей величине FV при заданной ставке процента.

,

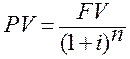где 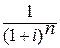- дисконтный множитель.

При наращении и капитализации процентов m раз в году формула имеет вид:

,

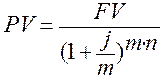где 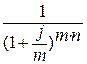- дисконтный множитель.

Разность FV – PV, в случае, когда PV определено дисконтированием, называют дисконтом. Обозначим его через D.

.

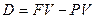Пример: Сумма 5 тыс. руб. выплачивается через 5 лет. Определить ее современную стоимость, если i = 12% годовых (для случая начисления процентов один и два раза в году).

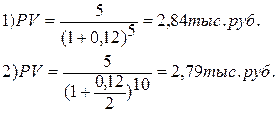
2) Учет по сложной учетной ставке. Дисконтирование по сложной учетной ставке осуществляется по формуле

,

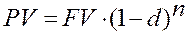где d – сложная годовая учетная ставка.

Пример: Долговое обязательство на сумму 5 млн. руб., срок оплаты которого наступает через 5 лет, продано с дисконтом по сложной учетной ставке 15% годовых. Каков размер полученной суммы за долг и величина дисконта (в тыс. руб.)?

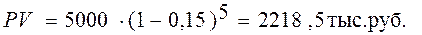
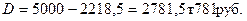
Номинальная и эффективная учетные ставки

Дисконтирование может производиться не один, а m раз в году, т.е. каждый раз учет производится по ставке f/m. В этом случае:

,

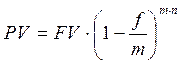где f – номинальная годовая учетная ставка.

Эффективная учетная ставка (d) характеризует степень дисконтирования за год. Определим ее на основе равенства дисконтных множителей:

,

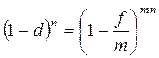Откуда

.

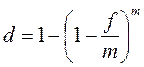В свою очередь

.

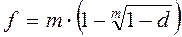Эффективная учетная ставка во всех случаях, когда m > 1, меньше номинальной.

Пример: Долговое обязательство на сумму 5 млн. руб., срок оплаты которого наступает через 5 лет. Определить сумму, полученную при поквартальном учете по номинальной учетной ставке 15%, и эффективную учетную ставку.

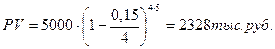
Эффективная учетная ставка составит:

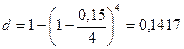или 14,17%

Наращение по сложной учетной ставке

Иногда наращенную сумму получают и с помощью сложной учетной ставки.

,

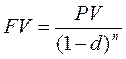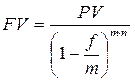
Множитель наращения при использовании сложной ставки d равен .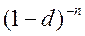

Определение срока ссуды и размера процентной ставки

Срок ссуды

1.1. При условии сложной годовой процентной ставки i и номинальной ставки j:

,

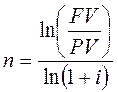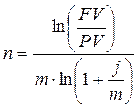
1.2. При условии сложной годовой учетной ставки d и номинальной учетной ставке f:

,

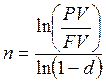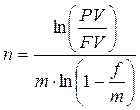
Пример: За какой срок в годах сумма, равная 75 млн. руб., достигнет 200 млн. руб. при начислении процентов по сложной ставке 15% раз в году и поквартально?

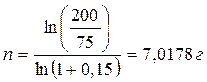
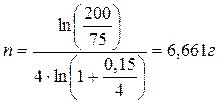
Размер ставки

2.1. При наращении по сложной годовой ставке процентов i и по номинальной ставке j:

,

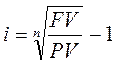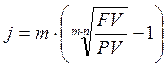
2.2. При дисконтировании по сложным учетным ставкам d и f :

,

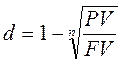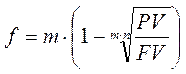
Пример: Сберегательный сертификат куплен за 100 тыс. руб., выкупная его сумма 160 тыс. руб., срок 2,5 года. Каков уровень доходности инвестиций в виде годовой ставки сложных процентов?

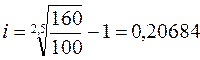или 20,684%.

Пример: Срок до погашения векселя равен 2 годам. Дисконт при его учете составил 30%. Какой сложной годовой учетной ставке соответствует дисконт?

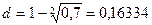или 16,334%.