Задания для самостоятельной работы. 1. Поменяйте условия задачи на предмет получения другого вида смеси (колбасы)

1. Поменяйте условия задачи на предмет получения другого вида смеси (колбасы).

1. Измените начальные параметры смеси и проанализируйте полученные изменения в себестоимости и отдельных компонентах.
2. Составьте самостоятельно задачу на получение смеси и оптимизацию ее себестоимости.
3. Измените количество компонентов и условий для смеси и рассмотрите трансформацию отчета по результатам.

Лабораторная работа №8
Тема: Расчет стоимости облигаций

Программное обеспечение:OS Windows, MS Excel, MS Word

Постановка целей занятия: познакомиться с финансовыми функциями по ценным бумагам и научиться их применять на практике.

Краткие теоретические сведения: Среди огромного разнообразия долгосрочных долговых обязательств, находящихся в обращении на отечественном и мировых финансовых рынках, следует особо выделить ценные бумаги, приносящие фиксированный доход (fixed income securities). Примерами подобных ценных бумаг являются облигации (bonds), депозитные сертификаты (deposit certificates), казначейские векселя (treasury bills) и некоторые другие виды обязательств, со сроком погашения свыше одного года . К этому виду ценных бумаг можно также отнести и привилегированные акции (preferred stocks), если по ним регулярно выплачивается фиксированный дивиденд.

Облигация, — согласно Федерального Закона «О рынке ценных бумаг», — это эмиссионная ценная бумага, закрепляющая право ее держателя на получение от эмитента облигации в предусмотренный ею срок ее номинальной стоимости и зафиксированного в ней процента от этой стоимости или иного имущественного эквивалента.

По сути, облигация является контрактом, удостоверяющим:

- факт предоставления ее владельцем денежных средств эмитенту;

- обязательство эмитента вернуть долг в оговоренный срок;

- право инвестора на получение регулярного или разового вознаграждения за предоставленные средства в виде процента от номинальной стоимости облигации или разницы между ценой покупки и ценой погашения.

Покупая облигацию, инвестор становится кредитором ее эмитента и получает преимущественное, по сравнению с акционерами, право на его активы в случае ликвидации или банкротства. Как правило, облигации приносят владельцам доход в виде фиксированного процента от номинала, который должен выплачиваться независимо от величины прибыли и финансового состояния заемщика.

Классификация облигаций достаточно разнообразна и зависит от положенного в ее основу признака.

В зависимости от эмитента, выделяют государственные, муниципальные (местных органов управления), корпоративные (предприятий и акционерных обществ) и иностранные (зарубежных заемщиков) облигации.

По физической форме выпуска облигации делятся на документарные (т.е. отпечатанные типографским способом, в виде бланков, сертификатов и т.д.) и бездокументарные (существующие в электронной форме, в виде записей компьютерных файлов на магнитных носителях).

По сроку обращения различают краткосрочные (до 1 года), среднесрочные (от 1 до 5 лет), долгосрочные (от 5 до 30 лет) и бессрочные облигации.

По форме выплаты дохода облигации делятся на купонные (с фиксированной или плавающей ставкой) и дисконтные (без периодических выплат доходов). Последние также часто называют облигациями с нулевым купоном (zero coupon bond). В ряде развитых стран имеют хождение облигации с выплатой процентов в момент погашения.

В общем случае, любая облигация имеет следующие основные характеристики: номинальная стоимость (par value, face value), купонная ставка доходности (coupon rate), дата выпуска (date of issue), дата погашения (date of maturity), сумма погашения (redemption value). Как будет показано ниже, важнейшую роль в анализе ценных бумаг играют дата и цена их приобретения, а также средняя продолжительность платежей (duration).

Номинальная стоимость – это сумма, указанная на бланке облигации, или в проспекте эмиссии.

Как правило, облигации выкупаются по номинальной стоимости. Однако текущая цена облигации может не совпадать с номиналом и зависит от ситуации на рынке.

Если цена, уплаченная за облигацию ниже номинала, говорят, что облигация продана со скидкой или с дисконтом (discount bond), а если выше – с премией (premium bond).

Для удобства сопоставления рыночных цен облигаций с различными номиналами в финансовой практике используется специальный показатель, называемый курсовой стоимостью или курсом ценной бумаги.

Купонная норма доходности – это процентная ставка, по которой владельцу облигации выплачивается периодический доход. Соответственно сумма периодического дохода равна произведению купонной ставки на номинал облигации и, как правило, выплачивается раз в год, полугодие или квартал.

Дата погашения – дата выкупа облигации эмитентом у ее владельца (как правило, по номиналу). Дата погашения указывается на бланке облигации. На практике в анализе важную роль играет общий срок обращения (maturity period) облигации, а также дата ее покупки (settlement date).

Общая формула стоимости облигации имеет следующий вид:

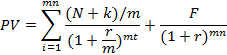
где F – сумма погашения (как правило – номинал, т.е. F = N); k – годовая ставка купона; r – рыночная ставка (норма дисконта); n – срок облигации; N – номинал; m – число купонных выплат в году.

Текущая стоимость облигации зависит от величины рыночной процентной ставки (требуемой нормы доходности) и срока погашения. Причем зависимость эта обратная. Из базовой модели оценки могут быть выведены две группы теорем.

Первая группа теорем отражает взаимосвязи между стоимостью облигации, ставкой купона и рыночной ставкой (нормой доходности):

- если рыночная ставка (норма доходности) выше ставки купона, текущая стоимость облигации будет меньше номинала (т.е. облигация будет продаваться с дисконтом);

- если рыночная ставка (норма доходности) меньше ставки купона, текущая стоимость облигации будет больше номинала (т.е. облигация будет продаваться с премией);

- при равенстве купонной и рыночной ставок текущая стоимость облигации равна номиналу.

Вторая группа теорем характеризует связь между стоимостью облигации и сроком ее погашения:

- если рыночная ставка (норма доходности) выше ставки купона, сумма дисконта по облигации будет уменьшаться по мере приближения срока погашения;

- если рыночная ставка (норма доходности) меньше ставки купона, величина премии по облигации будет уменьшаться по мере приближения срока погашения;

- чем больше срок обращения облигации, тем чувствительнее ее цена к изменениям рыночной ставки.

Рассмотрим два случая расчета цены и условий выплат облигаций:

1) стоимость облигации с фиксированной ставкой купона;

2) расчет по ценным бумагам с нарушением периодичности выплаты процентов.

Пример 1.

Срок обращения облигации с номиналом в 1000,00 составляет 10 лет. Ставка купона, выплачиваемая раз в год, равна 15%. Определить стоимость облигации, если:

а) рыночная ставка (требуемая норма доходности) равна 22%;

б) рыночная ставка (требуемая норма доходности) равна 10%.

Достижение поставленной цели осуществляется с использованием следующего алгоритма действий:

1) заполнить таблицу значениями, которые представлены на рис.1;

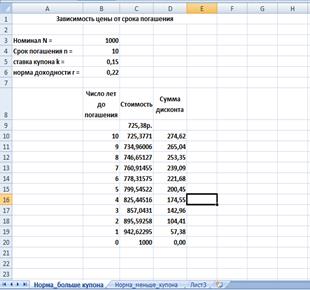
Рис.1 Фрагмент ЭТ для первого условия примера

2) Для того, чтобы получить значения, которые мы видим в ячейке С9, необходимо ввести следующую формулу: -ПС(B6;B4;B3*B5;B3)

3) Заполнить ячейки В10.В20 числами от 10 до 0.

4) Выделить блок ячеек В9.С20.

5) Выбрать из темы "Данные" главного меню блок "Работа с данными", далее «Анализ что-если» à «Таблица данных». На экране появится окно диалога (рис. 2).

6) Установить курсор в поле "Ячейка ввода столбца" и ввести имя ячейки, содержащей входной параметр (ячейка В4).

7) Нажать кнопку "ОК".

8) Ввести в ячейку D10 формулу: =1000-C10.

9) Скопировать ячейку D10 в блок D11.D20.

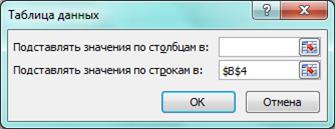
Рис.2 Таблица данных

Аналогичная таблица, реализующая расчеты для второго случая, представлена на рис. 3.

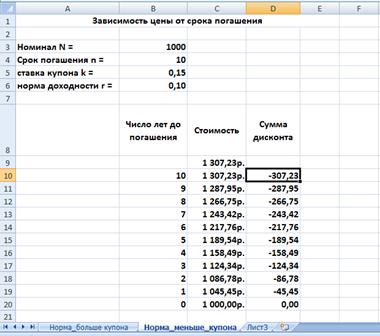
Рис. 3 Фрагмент ЭТ для второго условия примера

Краткие теоретические сведения по функциям ДОХОДПЕРВНЕРЕГ и ДОХОДПОСЛНЕРЕГ

Функция ДОХОДПЕРВНЕРЕГ () возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) первым периодом.

Примечание: Если данная функция недоступна или возвращает ошибку #ИМЯ?, установите и загрузите надстройку «Пакет анализа».

Синтаксис: ДОХОДПЕРВНЕРЕГ (дата_согл; дата_вступл_в_силу; дата_выпуска; первый_купон; ставка; цена; погашение; частота; базис)

Дата_согл — дата расчета за ценные бумаги (дата продажи ценных бумаг покупателю, более поздняя, чем дата выпуска).

Дата_вступл_в_силу — срок погашения ценных бумаг. Эта дата определяет момент, когда истекает срок действия ценных бумаг.

Дата_выпуска — дата выпуска ценных бумаг.

Первый_купон — дата первого купона для ценных бумаг.

Ставка — процентная ставка для ценных бумаг.

Цена— стоимость ценных бумаг.

Погашение — выкупная стоимость ценных бумаг за 100 рублей номинальной стоимости.

Частота — количество выплат по купонам за год. Для ежегодных выплат частота равна 1; для полугодовых — 2; для ежеквартальных — 4.

Базис — используемый способ вычисления дня.

Таблица 1

Вычисление дней для ввода значения в параметр Базис.

Базис	Способ вычисления дня
0 или опущен	Американский (NASD) 30/360
	Фактический/фактический
	Фактический/360
	Фактический/365
	Европейский 30/360

Замечания

- В Microsoft Excel даты хранятся в виде последовательности номеров, что позволяет выполнять над ними вычисления. По умолчанию день 1 января 1900 г. имеет номер 1, а 1 января 2008 — 39 448, так как интервал между этими датами составляет 39 448. В Microsoft Excel для компьютеров Макинтош по умолчанию используется другая система дат.

- Дата соглашения является датой продажи покупателю купона, например облигации. Срок платежа представляет собой дату истечения срока действия купона. Предположим, например, что облигация со сроком действия 30 лет выпущена 1 января 2008 г. и приобретена покупателем через шесть месяцев после выпуска. Датой выпуска будет 1 января 2008 г., датой расчета — 1 июля 2008 г., а срок погашения такой облигации наступит 1 января 2038 г., то есть через 30 лет после даты выпуска.

- Дата_согл, дата_вступл_в_силу, дата_выпуска, первый_купон и базис усекаются до целых.

- Если значение аргумента дата_согл, дата_вступл_в_силу, дата_выпуска или первый_купон не является допустимой датой, функция ДОХОДПЕРВНЕРЕГ возвращает значение ошибки #ЗНАЧ!.

- Если ставка < 0 или цена ≤ 0, то функция ДОХОДПЕРВНЕРЕГ возвращает значение ошибки #ЧИСЛО!.

- Если базис < 0 или базис > 4, то функция ДОХОДПЕРВНЕРЕГ возвращает значение ошибки #ЧИСЛО!.

- Должно выполняться следующее условие (в противном случае функция ДОХОДПЕРВНЕРЕГ возвращает значение ошибки #ЧИСЛО!):

- дата_вступл_в_силу > первый_купон > дата_согл > дата_выпуска

- В Microsoft Excel функция ДОХОДПЕРВНЕРЕГ вычисляется методом итераций. Используется метод Ньютона на основе формулы для функции ЦЕНАПЕРВНЕРЕГ. Доход вычисляется за 100 итераций пока вычисляемая цена для заданного дохода не станет близкой к значению аргумента «цена».

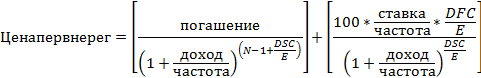
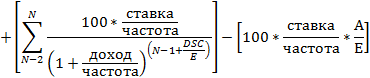
где:

- A = количество дней от начала периода купона до даты расчета (накопленные дни).

- DSC = количество дней от даты расчета до даты следующего купона.

- DFC = количество дней от начала периода нерегулярного купона до даты первого купона.

- E = количество дней в периоде купона.

- N = количество оплачиваемых купонов между датой расчета и датой погашения. (Если это число является дробным, то оно округляется с избытком до ближайшего целого).

Пример.

Определите доход от размещения облигаций с номиналом в 100 руб. при купонной ставке 5,75%, покупной цене 84,5 руб. Облигация была куплена 11 ноября 2008 года и должна погаситься 1 марта 2021 при полугодовой выплате процентов (частота = 2). Используйте 0 тип базиса. См. Таблицу 2.

Таблица 2

Исходные данные

Данные	Описание (результат)
11 ноября 2008 г.	Дата соглашения
1 марта 2021 г.	Дата вступления в силу
15 октября 2008 г.	Дата выпуска
1 марта 2009 г.	Дата первого купона
5,75%	Процентная ставка по купонам
84,50	Цена
	Выкупная стоимость
	Частота полугодовая (см. выше)
	Базис 30/360 (см. выше)
Формула	Описание (результат)
=ДОХОДПЕРВНЕРЕГ(A2;A3;A4;A5;A6;A7;A8;A9;A10)	Доход по облигации с нерегулярным (коротким или длинным) первым периодом (0,077245542 или 7,72%)

Алгоритм работы выполнения задания.

1) Создадим таблицу в Excel и заполним ее значениями, как представлено в вышестоящей таблице.

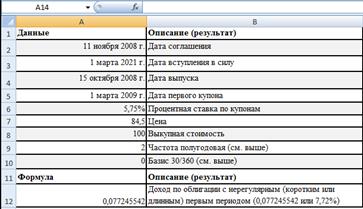
Рис. 4 Окно таблицы расчета

2) В ячейку А12 введем формулу ДОХОДПЕРВНЕРЕГ ().Для этого в строке ввода формул выберем ДОХОДПЕРВНЕРЕГ ()(Рис. 5).

3) После выбора необходимых ячеек нажмем ОК на окне рис.5 и получим результат. Рис. 6

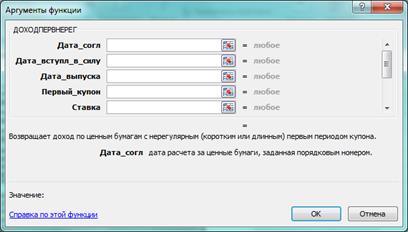
Рис. 5 Главное окно функции

Рис. 6 Результат расчета и формула

Таким образом, на вложенные нами при покупке облигации средства 84,5 руб., мы заработаем 7,72% в год.

ДОХОДПОСЛНЕРЕГ - Возвращает доход по ценным бумагам с нерегулярным (коротким или длинным) последним периодом.

Синтаксис: ДОХОДПОСЛНЕРЕГ (дата_согл; дата_вступл_в_силу; последняя_выплата; ставка; цена; погашение; частота; базис)

Дата_согл – дата расчета за ценные бумаги (более поздняя, чем дата выпуска, когда ценные бумаги были проданы покупателю).

Дата_вступл_в_силу – срок погашения ценных бумаг. Эта дата определяет момент истечения срока действия ценных бумаг.

Последняя_выплата– дата последнего купона для ценных бумаг.

Ставка – процентная ставка для ценных бумаг.

Цена – стоимость ценных бумаг.

Погашение – выкупная стоимость ценных бумаг за 100 грн. номинальной стоимости.

Частота – количество выплат по купонам за год. Для ежегодных выплат частота = 1; для полугодовых выплат частота = 2; для ежеквартальных выплат частота = 4.

Базис – используемый способ вычисления дня.

Базис	Способ вычисления дня
0 или опущен	Американский (NASD) 30/360
	Фактический/фактический
	Фактический/360
	Фактический/365
	Европейский 30/360

ДОХОДПОСЛНЕРЕГ вычисляется следующим образом:

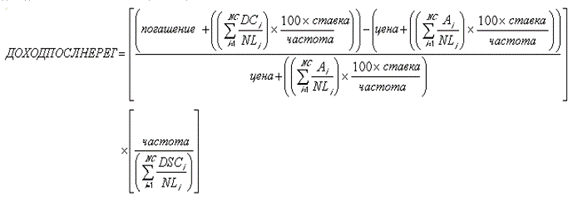
где:

A_i = количество накопленных дней для i‑го или последнего квазикупонного периода в нерегулярном периоде, отсчитанное вперед от даты последней выплаты перед погашением.

DC_i = количество дней, сосчитанных для i‑го или последнего квазикупонного периода, разделенное на продолжительность фактического купонного периода.

NC = количество квазикупонных периодов, укладывающихся в нерегулярный период. Если это число является дробным, то оно округляется с избытком до ближайшего целого.

NL_i = нормальная продолжительность в днях i‑го или последнего квазикупонного периода в нерегулярном купонном периоде.

Пример: Рассчитать доход облигации, есть номинальная стоимость 100 руб., при купонной ставке 3,75%, покупной цене 99,875руб. Облигация была куплена 20 апреля 2008 года, дата последней выплаты 24 декабря 2007 года согласно таблице 3.

Таблица 3

Исходные данные для решения задачи

Данные Описание 20 апреля 2008 г. Дата соглашения 15 июня 2008 г. Дата вступления в силу 24 декабря 2007 г. Дата последней выплаты 3,75% Процентная ставка по купонам 99,875р. Цена 100р. Выкупная стоимость Частота полугодовая (см. выше) Базис 30/360 (см. выше) Формула Описание (результат) =ДОХОДПОСЛНЕРЕГ(A2;A3;A4;A5;A6;A7;A8;A9) Доход по облигации с нерегулярным (коротким или длинным) последним периодом (0,045192)

Алгоритм решения поставленной задачи аналогичен вышеописанному. Реализуйте действие данное самостоятельно.