Рыночные подходы к оценке эффективности инвестиций: компондирование и дисконтирование
Переход к рыночной экономике в нашей стране объективно вызвал и необходимость изменения подходов к оценке эффективности инвестиций.
Если в условиях государственной экономики использование метода аннуитета (средних величин) еще как-то было оправдано: поскольку цены на продукцию, а следовательно и себестоимость и прибыль годами не изменялись и были постоянными, то в рыночной экономике колебания цен в зависимости от конъюнктуры рынка могут быть весьма значительными и использование в расчетах «средних» величин становится все более бессмысленным. Естественным выходом из этой ситуации является переход на метод денежных потоков (Cash flow – CF), когда все исходные данные: инвестиции, объемы продаж, себестоимость, прибыль и другие задаются не в виде постоянных «средних» величин (чаще всего среднегодовых), а виде изменяющихся во времени показателей.
Однако, как только мы начинаем описывать экономические процессы (показатели) во времени, мы тут же сталкиваемся с необходимостью каким-образом решить возникающую проблему фактора времени (ФВ).
Дело в том, что в рыночной экономике любые деньги выступают как потенциальный капитал, т.е. если их куда-либо вложить, то они с течением времени могут приносить доход. Следовательно, любая, условно говоря «тысяча» долларов (евро, рублей …) сегодняшних, через год можем стать суммой «тысяча сто» или даже большей. Поэтому грамотный экономист всегда оценивает деньги в зависимости от того, когда они будут получены (или затрачены).
Для разъяснения этого тезиса рассмотрим пример.
«При изучении наук примеры полезнее правил»
И. Ньютон; английский математик
ПРИМЕР 1.
Финансовый брокер предлагает Вам купить облигации эмитента А по цене 140 USD за облигацию на следующих условиях: номинал облигации 100 USD, ежегодный купон 20%, обращение – 3 года, после это «гашение» облигации по номиналу.
Пояснение. Купон характеризует доходность облигаций; выплаты по облигациям (в отличие от акций) обязательны; инфляция здесь не рассматривается.
РЕШЕНИЕ.
Если не брать во внимание влияние фактора времени, то будущие доходы покупателя (инвестора) за три года можно сосчитать следующим образом.
| Доходы | 1 год | 2 год | 3 год | Всего |
| 1. Выплаты по купону 2. Гашение по номиналу | - | - | ||
| Итого |
Сравнивая полученный за три года доход (160 USD), с ценой приобретения (140 USD) можно сделать «ложный» вывод, что инвестор заработает (плюс) 20 USD и поэтому облигации покупать можно.
Однако, если вы критически настроенный человек, то Вас будет терзать червь сомнений: ведь 140 долларов надо отдать сейчас «сегодня», а доходы Вы будете получать: 20 долларов через год, следующие 20 долларов через два года, 120 долларов через три!
Всем своим нутром и душой мы чувствуем, что сегодняшние «деньги» важней и ценней чем деньги «завтрашние», поэтому неправомерно с точки зрения грамотного экономиста суммировать их непосредственно; желательно и нужно их привести их к сопоставимому виду. Такую операцию приведения можно осуществить, используя известную формулу так называемых «сложных процентов».
1. Формула сложных процентов: компондирование и дисконтирование.
Хотя формула сложных процентов хорошо известна, не откажем себе в удовольствии вывести ее.
Введем обозначения:
Дс – деньги «сегодня»;
Дз – деньги «завтра»;
Т- время (например, количество лет, которое «работают» деньги);
Е – коэффициент эффективности, с которой «работают» размещенные в какой-либо бизнес деньги.
Представим, что мы имея какие-то деньги (Дс) размещаем их в некий проект (бизнес, банк, ценные бумаги…), где эти деньги «работают» с эффективностью Е; при этом сумма денег ежегодно у нас возрастает на величину Е и мы все это время деньги из оборота не вынимаем. Рассчитаем, как будет возрастать сумма наших денег во времени.
| Время | Формирование суммы денег во времени | В универсальном виде |
| 0 – старт проекта | Дс | Дс(1+Е)0 |
| 1 – прошел 1 год | Дс + Дс * Е | Дс(1+Е)1 |
| 2 – прошло 2 года | Дс + Дс * Е+( Дс + Дс * Е)*Е= Дс + Дс * Е+Е* Дс + Дс * Е2= Дс+2 Дс * Е+ Дс* Е2 | Дс(1+Е)2 |
| … | … | … |
| t – прошло t лет | Дс(1+Е)t |
Отсюда мы и получаем знаменитую формулу сложных процентов:
Дз = Дс * (1+ Е)t (1)
Вычисление по формуле (1) называется «компондирование» и широко используется в экономических расчетах. Например, по этой формуле вы можете рассчитать, сколько денег вы «заработаете» в течение определенного периода лет, разместив их на депозит (срочный вклад) в банке.
Замечательное свойство формулы (1) в том, что в разных ее сторонах через знак равенства связаны между собой деньги «завтра» (Дз) и деньги «сегодня» (Д  с). Это позволяет нам с успехом оценивать не только сегодняшние деньги в будущем, но и будущие деньги «переводить» в сегодняшние, а именно:
с). Это позволяет нам с успехом оценивать не только сегодняшние деньги в будущем, но и будущие деньги «переводить» в сегодняшние, а именно:
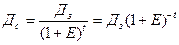 (2)
(2)
Вычисление по формуле (2) называется дисконтирование, от discount (анг.) – скидка, уменьшение.
В инвестиционном анализе, в оценке эффективности инвестиций используется, прежде всего, именно формула (2); инвестор, оценивая будущие доходы, хочет знать их сегодняшнюю стоимость, что бы сравнить ее с величиной сегодняшних инвестиций. Зная формулу (2) вернемся вновь к решению примера 1.
ПРИМЕР 1. (Продолжение)
Представим будущие доходы (выплаты) по облигациям в виде денежного потока по годам:
USD
| Наименование | |||
| 1. Доходы |
Приведем будущие доходы инвестора на сегодняшний день, используя чуть преобразованную формулу (2):
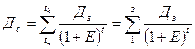 (3)
(3)
Значения Дз по годам нам известны, но возникает новый вопрос с выбором величины коэффициента Е?
Коэффициент Е, как следует вышесказанного, отражает эффективность с которой работают или могут работать вложенные куда-либо деньги (инвестиции).
Понятно, что в развитой рыночной экономике существует множество возможностей, куда вложить деньги, а, следовательно, имеют место и большие различия в коэффициентах эффективности. Выбор той или иной точки приложения капитала зависит от умения, возможностей, целей и желания инвестора. Таким образом, для решения Примера 1 с использованием формулы 3 мы для выбора коэффициента Е должны понять: кто такой наш инвестор, какими знаниями и возможностями он располагают и какого его поведение на рынке? Для того, чтобы выполнить расчеты, допустим, что наш инвестор (покупатель облигации) – это рядовой обыватель, не занимающийся бизнесом, не желающий рисковать и консервативно настроенный на получение пусть и небольшого дохода, но с высокой гарантией. Логично предположить тогда, что реальной альтернативой для него будет размещение денег на депозиты коммерческих банков. Если по депозитам банка уровень годовой доходности колеблется в пределах 10%, то именно эту величину Е и возьмет в расчеты примера 1 наш инвестор (Е=10% или Е=0,1) или мы это сделаем за него.
Подставляя эти данные в формулу (3) получим:
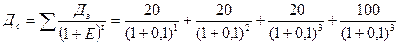 =
=
18,2+16,5+15,0+75,1=124,8 USD
Сравнивая величину доходов по облигации (124,8) с величиной цены покупки (140 USD) приходим к выводу, что для данного инвестора сальдо сделки (проекта) отрицательное (+124,8-140=-15,2 USD) – поэтому облигации ему покупать невыгодно (экономически нецелесообразно).
Как видим, решение Примера 1 с учетом фактора времени привело нас к совершенно противоположным выводам относительно возможности инвестирования! В англоязычной литературе стоимость будущих доходов, приведенная на сегодня обозначается аббревиатурой PDV, что означает Present Discounted Value - приведенная на сегодня стоимость.
Тема № 4
