Анализ чувствительности
Одной из задач анализа проектаявляется определение чувствительности показателей эффективности к изменениям различных параметров.
Необходимо анализировать устойчивость проекта к возможным изменениям как экономической ситуации в целом (изменение структуры и темпов инфляции, увеличение задержки платежей), так и внутренних показателей проекта (изменение объемов сбыта, цены продукции). Такой анализ называется анализом чувствительности.
Чем шире диапазон параметров, в котором показатели эффективности остаются в пределах приемлемых значений, тем выше «запас прочности» проекта, тем лучше он защищен от колебаний различных факторов, оказывающих влияние на результаты реализации проекта.
Исследование чувствительности показателей эффективности к изменению ставки дисконтирования позволяет определить устойчивость проекта по отношению к колебаниям конъюнктуры финансового рынкаи возможным изменениям макроэкономических условий деятельности. Для анализа чувствительности необходимо:
• выбрать основные показатели (NPV, IRR, FV ит. д.), изменение которых существенно отразится на потоках проекта;
• проанализировать при изменении уровня факторов (изменение выручки, себестоимости, затрат на зарплату, налоги и т. д.), какой из показателей будет наиболее чутким к этим изменениям и какой фактор оказывает самое большое воздействие на модель;
• проверить чувствительность выбранного показателя при вероятности отклонений первого (вероятность того, что фактор изменится, т. е. станет больше, меньше или останется плановым) и второго уровней (если фактор все же окажется ниже планового уровня, то с вероятностью 60 % отклонение будет не более 10 %).
48. МЕТОД МОНТЕ‑КАРЛО
Цель статистического анализа– определить степень воздействия случайных факторов на показатели эффективности проекта.
Анализ производится следующим образом.Допустим, определено, какие именно данные следует признать неопределенными, а также установлен диапазон значений, в пределах которого они могут изменяться случайным образом. Если речь идет, например, о двух параметрах, это означает, что определена область значений исходных данных, имеющая форму прямоугольника. Для трех переменных эта область представляет собой параллелепипед. Совокупность исходных данных, от которых зависит судьба проекта, отображается точкой, лежащей внутри выделенной области. Таких точек великое множество, поэтому выполнить расчет проекта для каждой из них невозможно. Тем не менее необходимо определить, какое воздействие оказывает неопределенность исходных данных на поведение модели. Эта задача решается с помощью метода Монте‑Карло.
Предположим, в нашем распоряжении имеется способ выбирать точки в выделенной области данных случайным образом, аналогичный рулетке в игорном заведении. Для каждой выбранной таким способом точки мы проведем расчет показателей эффективности и запишем их в таблицу. Проделав достаточно большое количество опытов, мы можем подвести некоторые итоги.
Для количественной оценки результатов используются два критерия. среднее значение и неопределенность. Предположим, мы проделали Nопытов и получили набор значений некоторого показателя f(n= 1, N). Тогда среднее значение Mопределяется по формуле
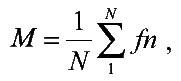
где М– ожидаемое значение величины fn; f– некий исследуемый показатель; N– количество проделанных опытов.
Неопределенность (или коэффициент вариации) рассчитывается следующим образом:
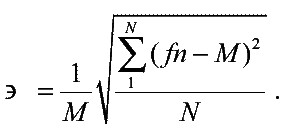
Величину Мможно интерпретировать как ожидаемое значение случайной величины fn.
Неопределенность можно рассматривать также как оценку риска, связанного с тем, что значение fn отклонится от ожидаемой величины М.
