Корреляционно-регрессионный анализ

С помощью корреляционно-регрессионного анализа выявляется теснота связи, тип зависимости (прямолинейная, параболическая и т.д.), рассчитываются уравнения и определяется влияние каждого анализа. В отличии от детерминированных методов, которые используются для жесткой взаимосвязи, предложенные модели могут учитывать только часть влияния факторов, а не все 100%.

ПР = 3,6Ф_в – 1,2УТК + 48,7В.

где ПР – прибыль, Ф_в – фондовооруженность, УТК – уровень текучести кадров, В – выработка.

Корреляционно-регрессионный анализ (КРА) используется в стохастических (вероятностных) системах. Он состоит в выявлении тесноты связи между показателями, определении вида связи и влияния факторов. Данный метод используют, например, для исследований на уровне региона. Особенность этого метода состоит в том, чтовыявленные с его помощью закономерности справедливы только для тех условий, для которых они определялись (т. е. для условий, в которых были получены исходные показатели для анализа). Таким образом, необходимо каждый раз самостоятельно выявлять закономерности для тех условий, которые интересуют исследователя. Так, например, с помощью метода корреляционно-регрессионного анализа были получены Z-счета Альтмана, применяемые для определения вероятности банкротства. Но поскольку они были рассчитаны на основании данных о деятельности ста крупнейших акционерных обществ США, распространять их на малые предприятия нельзя (более того, и на крупных предприятиях России их тоже применять некорректно, поскольку условия экономической деятельности в этих странах разные).

Необходимым условием применения данного метода является то, что объем информации (т. е. количество периодов, за которые имеются данные) должен превосходить количество факторов в два-три раза, причем всего должно быть не менее 20 точек для построения теоретической кривой.

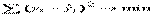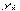В основе метода корреляционно-регрессионного анализа лежит метод наименьших квадратов (МНК). В соответствии с МНК для любых фактических данных всегда можно найти такую теоретическую кривую, которая пройдет через максимальное количество точек (отражающих фактические данные). Отсюда сумма квадратов отклонений фактических данных от теоретической кривой будет минимальной, т. е. , где и 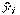- фактические и теоретические значения признака соответственно. Для каждого вида теоретической кривой существует своя система нормальных уравнений.

Для прямой 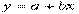система нормальных уравнений выглядит следующим образом:

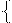
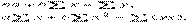
где n – количество данных.

ŷ (теоретическое значение y) определяем на основе уравнения регрессии, коэффициенты которого рассчитывают с помощью системы нормальных уравнений.

При выборе теоретической кривой в КРА для каждого вида кривой рассчитывают среднюю ошибку аппроксимации 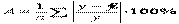. Для выбранной нами линейной зависимости А=0,015 или 1,5%. Для грубого приближения регрессии к реальной зависимости ошибка не должна превышать 12-15%. Выбирается тот вид теоретической кривой, для которого ошибка оказалась наименьшей. На последнем этапе проводят оценку надежности по критерию Фишера. Если при заданном уровне значимости 0,05 расчетное значение критерия больше табличного, то полученное уравнение регрессии признается значимым. Задача 2