Функции «Процентный платеж» (ПРПЛТ) и «Основной платеж» (ОСПЛТ)
Функция ПРПЛТ вычисляет за отдельный учетный период сумму выплаты процентов с учетом ставки процентов, начальной и накопленной суммы, периодического платежа, периодичности платежей (или капитализации) и срока договора. Синтаксис функции:=ПРПЛТ(ставка; период; кпер; пс; бс; тип).
Функция ОСПЛТ вычисляет за отдельный учетный период сумму накопления вклада или погашения долга с учетом ставки процентов, начальной и накопленной суммы, суммы периодического платежа, периодичности платежей (или капитализации) и срока действия договора. Синтаксис функции:= ОСПЛТ(ставка; период; кпер; пс; бс; тип)
За один и тот же период величина (ПРПЛТ + ОСПЛТ) остается неизменной, изменяется только соотношение этих компонентов в различные периоды.
Пример 14.
Сумма 2000р. размещены на депозитном счете сроком на 4 года под 10% годовых, дополнительные вложения осуществляются в конце года. Сумма накоплений составит 6000 р. Период капитализации - год.
Постоянный ежегодный платеж вычисляется с помощью функции ПЛТисоставляет -661,88р.
Соотношение ПРПЛТ и ОСПЛТ по периодам:
| Год | ПРПЛАТ | ОСПЛТ | ИТОГО (ПЛТ) |
| 200,00р. | -861,88р. | -661,88р. | |
| 286,19р. | -948,07р. | -661,88р. | |
| 381,00р. | -1042,88р. | -661,88р. | |
| 485,28р. | -1147,17р. | -661,88р. |
Значение ПРПЛАТ положительное, так как это проценты, которые начисляются за пользованием вкладом.
Значение ОСПЛТ отрицательное, так как за счет дополнительного взноса и остающихся в распоряжении банка суммы по процентам увеличивается общая сумма накопления.
Пример 15.
Взят кредит 10000 р. сроком на 5 лет под 20% годовых. Период капитализации - год.
Определить по периодам:
· суммы выплат,
· изменение суммы долга,
· структуру выплат процентов за пользование кредитом и в счет погашения долга,
· сумму выплат процентов за пользование кредитом и в счет погашения долга.
Изобразить графически полученные соотношения.
Пример 16.
На депозитном счете размещена сумма 10000 р. сроком на 5 лет под 10% годовых. Сумма накопления составит 18000 р. Период капитализации - год.
Определить по периодам:
· суммы выплат,
· сумму на счете,
· структуру начисления процентов и увеличения суммы накопления.
· Изобразить графически полученные соотношения.
Функции «Накопительный процентный платеж» (ОБЩПЛАТ) и «Накопительный доход» (ОБЩДОХОД)
Функция ОБЩПЛАТ вычисляетсумму процентов за интервал учетных периодов (начальный – конечный), является итогом для смежных учетных периодов, вычисленных с помощью функции ПРПЛТ. Синтаксис функции:
= ОБЩПЛАТ(ставка; кпер; пс; начальный_период; конечный_период; тип)
Функция ОБЩДОХОД вычисляет сумму накопления (выплаты долга) за интервал учетных периодов(начальный – конечный), является итогом для смежных учетных периодов, вычисленных с помощью функции ОСПЛТ. Синтаксис функции:
= ОБЩДОХОД(ставка; кпер; пс; начальный_период; конечный_период; тип)
Эти функции имеют специфику вычисления:
- Для погашения кредита (ссуды) величины ОБЩПЛАТ и ОБЩДОХОД — отрицательные.
- Для расчетов по депозитному счету в функциях ОБЩПЛАТ и ОБЩДОХОД значение параметра начальной суммы вклада указывается как положительное число. Вычисляемое значение ОБЩДОХОД показывает накопленную сумму дополнительных взносов и процентов за интервал времени.
- К концу любого n-го учетного периода (N — общее число периодов договора, начальный период равен 1) выполняется соотношение:
ОБЩПЛАТn + ОБЩДОХОДn = n* ПЛТ n = 1 N.
Эта сумма показывает накопленную сумму выплат в интервале от начала договора до текущего учетного периода.
Пример 17.
Взят кредит 10000 р. сроком на 5 лет под 20% годовых. Определить за каждый интервал: первый год, первые два года, первые три года, за весь срок (четыре года):
- суммы выплат,
- изменение суммы долга,
- сумму выплат процентов за пользование кредитом и в счет погашения долга.
Изобразить графически полученные соотношения.
Пример 18.
На депозитном счете размещена сумма 10000 р. сроком на 5 лет под 10% годовых. Сумма накопления составит 18000 р. Определить за каждый интервал: первый год, первые два года, первые три года, за весь срок (четыре года):
- суммы выплат,
- изменение суммы вклада,
- сумму процентов и накоплений.
Изобразить графически полученные соотношения.
Непериодические или нефиксированные платежи, переменная ставка процентов
Если платежи непериодические, а величина платежа — переменная (рис.8), денежный поток представляется в виде потоков за каждый период (вход - выход).
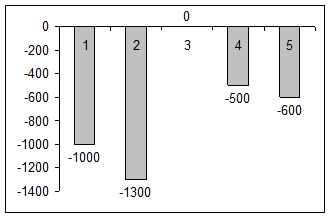
Рисунок 8
Пример 19.
Вычислить сумму накопления на депозитном счете за 4 года, если начальная сумма составляет 1000 р. с последующим вложением средств по схеме:
| Период | Сумма в начале периода | Ставка процентов за период | Формула расчета наращенной суммы | Наращенная сумма | Сумма вложений | Сумма в конце периода |
| 1000,00 | 10% | =БС(10%;1;-1000;-1000;0) | 1 100,00р. | 2100,00 | ||
| 2100,00 | 9% | =БС(9%;1;-1300;-2100;0) | 2 289,00р. | 3589,00 | ||
| 3589,00 | 6% | =БС(6%;1;0;-3589;0) | 3 804,34р. | 3804,34 | ||
| 3804,34 | 5% | =БС(5%;1;-500;-3804,34;0) | 3 994,56р. | 4494,56 |
Пример 20.
Вычислить сумму накопления на депозитном счете за 6 лет, если начальная сумма составляет 3000 р. с последующим вложением средств по схеме:
| Период | Сумма взноса | Ставка процентов |
| -500 | 10% | |
| 10% | ||
| -500 | 9% | |
| 9% | ||
| -500 | 8% | |
| 8% |
Вычислить эквивалентную постоянную ставку процентов для средней суммы дополнительного периодического платежа.
