Сопоставление линии рынка ценных бумаг и линии рынка капитала
Наиболее простая и наглядная интерпретация взаимосвязи доходности инвестиции с ее систематическим риском дана в широко известной и популярной в финансовом мире модели САРМ, которая была разработана У. Шарпом.
Модель САРМ представляет собой теорию, призванную объяснить, какими должны быть премии за риск, на которые согласились бы инвесторы в ситуации рыночного равновесия при условии, что все они обладают равными возможностями, ведут себя рационально, стремятся диверсифицировать свои портфели и при их формировании руководствуются одинаковы ми прогнозами относительно ожидаемых доходностей, их вариабельности (стандартных отклонений) и взаимозависимостей (корреляций).
Портфель рисковых активов любого инвестора независим общего объема вложенных в него средств в условиях равновесия спроса и предложения по своей структуре будет точной копией рынка в целом. Поскольку невозможно построить портфель более диверсифицированный, чем рынок в целом, он будет представлять собой эталон, или идеал, диверсификации и содержать только систематический, или рыночный, риск.
Портфель М, включающий все существующие активы и структурно копирующий рынок, называется рыночным. Очевидно, что его ожидаемая доходность 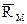 и риск
и риск 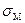 будут соответствовать среднерыночным значениям.
будут соответствовать среднерыночным значениям.
Предположим, на рынке существует хотя бы один безрисковый актив F, например ценные бумаги, эмитированные государством. Такой актив обеспечивает получение за период владения некоторого гарантированного уровня доходности 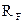 , при этом его риск равен нулю, т. е.
, при этом его риск равен нулю, т. е. 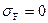 .
.
Рассмотрим портфель, построенный комбинированием рыночного портфеля М с безрисковым активом F. Определим ожидаемую доходность такого портфеля:
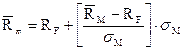 . (1)
. (1)
Выражение (1) задает прямую линию получившую название «линия рынка капитала» (Capital Market Line –CML) с началом в точке с координатами (0, 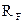 ) и проходящую через точку (
) и проходящую через точку ( 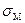 ,
, 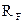 ), т.е. местоположение рыночного портфеля (рисунок 4). Рассмотрим ее свойства более детально.
), т.е. местоположение рыночного портфеля (рисунок 4). Рассмотрим ее свойства более детально.
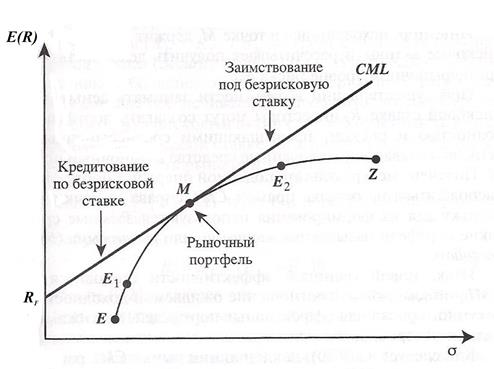
Рисунок 4 – Линия рынка капитала CML [1, с. 415]
Возможность проводить операции с безрисковыми активами позволяет инвесторам создавать новые варианты портфелей, сочетающих рисковые и безрисковые вложения. Таким образом, они могут выбирать любые комбинации риска и доходности, находящиеся на прямой CML. При этом, как следует из приведенного графика, все портфели, попадающие на линию CML, предпочтительнее, чем портфели, попадающие на кривую EZ, за исключением точки М (т. е. рыночного портфеля). Следовательно, все точки прямой CML представляют собой наилучшие возможные комбинации риска и доходности.
Наличие безрискового актива приводит к тому, что теперь рациональные инвесторы будут выбирать портфели, лежащие на эффективной линии рынка CML.
Инвестор, находящийся в точке 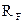 , вложил свои средства в безрисковые активы и рассчитывает на получение гарантированного дохода.
, вложил свои средства в безрисковые активы и рассчитывает на получение гарантированного дохода.
Портфели, попадающие на отрезок 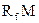 , состоят из комбинаций вложений в рисковые и безрисковые активы. Они называются ссудными, поскольку, вкладывая средства в государственные бумаги, инвестор фактически ссужает деньги правительству по безрисковой ставке
, состоят из комбинаций вложений в рисковые и безрисковые активы. Они называются ссудными, поскольку, вкладывая средства в государственные бумаги, инвестор фактически ссужает деньги правительству по безрисковой ставке 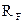 .
.
Инвестор, находящийся в точке М, держит в портфеле только рисковые активы и рассчитывает получить доходность 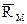 при среднерыночном уровне риска
при среднерыночном уровне риска 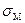 .
.
При существовании возможности занимать деньги по безрисковой ставке 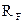 инвесторы могут создавать портфели с доходностью и риском, превышающими среднерыночный уровень, вкладывая заимствованные средства в рыночный портфель М. Полученные в результате подобной операции портфели будут располагаться на отрезке прямой CML справа от точки М. Поскольку для их формирования используются заемные средства, такие портфели называются заемными, или рычаговыми.
инвесторы могут создавать портфели с доходностью и риском, превышающими среднерыночный уровень, вкладывая заимствованные средства в рыночный портфель М. Полученные в результате подобной операции портфели будут располагаться на отрезке прямой CML справа от точки М. Поскольку для их формирования используются заемные средства, такие портфели называются заемными, или рычаговыми.
Итак, новой границей эффективности становится линия СМL, описывающая соотношение ожидаемой доходности и совокупного риска для эффективных портфелей, достижимых при наличии безрискового актива.
Как следует из (1), наклон линии рынка CML равен выражению в скобках. При этом числитель 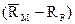 характеризует превышение доходности рыночного портфеля над безрискововой ставкой. Это премия за риск инвестирования в рыночный портфель М, состоящий из рисковых активов.
характеризует превышение доходности рыночного портфеля над безрискововой ставкой. Это премия за риск инвестирования в рыночный портфель М, состоящий из рисковых активов.
Знаменатель представляет собой риск рыночного портфеля. Таким образом, наклон прямой CML показывает величину премии за «единицу» рыночного риска. Другими словами, наклон линии рынка определяет требуемую дополнительную доходность на каждую дополнительную единицу рыночного риска, или награду (плату) за риск.
Можно показать, что для отдельного актива i равновесная взаимосвязь между риском и доходностью в CAMP будет иметь вид:
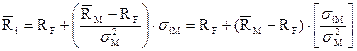 , (2)
, (2)
где 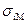 - ковариация актива i с рыночным портфелем М.
- ковариация актива i с рыночным портфелем М.
Уравнение (2), описывающее прямую с началом в точке (0, 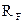 ) и наклоном
) и наклоном 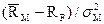 , получило название рыночной линии ценной бумаги (Security Market Line – SML). Как следует из (2), активы с большим значением ковариации с рыночным портфелем должны обеспечивать большую доходность. Нетрудно также заметить, что рисковый актив с
, получило название рыночной линии ценной бумаги (Security Market Line – SML). Как следует из (2), активы с большим значением ковариации с рыночным портфелем должны обеспечивать большую доходность. Нетрудно также заметить, что рисковый актив с 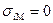 будет иметь доходность, равную безрисковой ставке
будет иметь доходность, равную безрисковой ставке 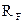 , а рисковый актив с
, а рисковый актив с 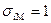 будет иметь доходность рыночного портфеля
будет иметь доходность рыночного портфеля 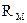 .
.
Графическая интерпретация взаимосвязи между рыночным риском и доходностью актива, отражаемая SML, представ на рисунке 5.
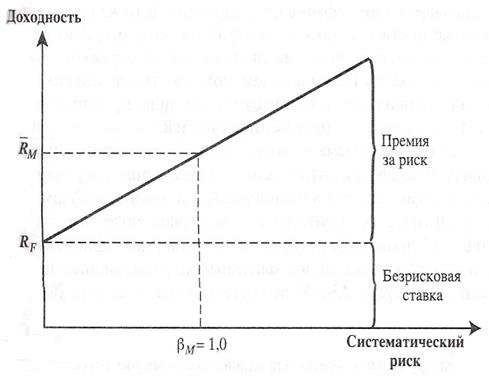
Рисунок 5 – Графическая интерпретация SML [1, с.419]
Обозначим 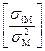 в (2) через
в (2) через 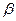 и перепишем формулу следующим образом:
и перепишем формулу следующим образом:
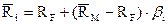 . (3)
. (3)
Уравнение (3) является окончательной формулировкой модели САРМ и альтернативным способом задания прямой SML. Выражение в квадратных скобках известно как коэффициент, или индекс, «бета», используемый в САРМ в качестве количественной меры систематического риска. Нетрудно показать, что для рыночного портфеля M этот коэффициент равен 1:
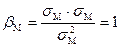 . (4)
. (4)
Таким образом, коэффициент, равный 1, отражает среднюю степень риска, сложившегося на рынке ценных бумаг. Если для конкретного актива значение коэффициента 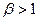 , он является более рисковым по сравнению с рынком в целом, при
, он является более рисковым по сравнению с рынком в целом, при 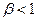 - менее рисковым. Для безрисковой инвестиции
- менее рисковым. Для безрисковой инвестиции 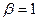 .
.
Основным достоинством САРМ является наглядное представление взаимосвязи риска и доходности. Согласно (3) доходность рискового актива i равна безрисковой ставке 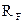 плюс премия за риск. В свою очередь, премия за риск равна его цене
плюс премия за риск. В свою очередь, премия за риск равна его цене 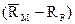 , умноженной на его количество
, умноженной на его количество 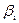 .
.
Несмотря на значительную условность базовых допущений, модель САРМ получила широкое распространение в финансовом и инвестиционном менеджменте, а ее автор У. Шарп в 1990 г. был удостоен Нобелевской премии в области экономики.
Список литературы
1. Лукасевич И.Я. Финансовый менеджмент: учебник / И.Я. Лукасевич. – М.: Эксмо, 2008. – 768 с.
2. Поляк Г.Б. Финансовый менеджмент: учебник / Г.Б. Поляк. – М.: ЮНИТИ, 2003. – 264 с.
