ВОПРОС 5: Факторный анализ и его теоретические составляющие. Понятие, типы и задачи факторного анализа. Способы измерения влияния факторов в детерминированном анализе

1. Понятие, типы и задачи факторного анализа.

2. Способы измерения влияния факторов в детерминированном анализе.

1.

Каждый результативный показатель зависит от многочислен­ных и разнообразных факторов. Чем более детально исследуется влияние факторов на величину результативного показателя, тем точнее результаты анализа и оценка качества работы предприя­тий. Отсюда важным методологическим вопросом в анализе яв­ляется изучение и измерение влияния факторов на величину ис­следуемых экономических показателей.

Под факторным анализом (диагностикой) понимается методика и системного изучения и измерения воздействия факторов на величину результативных показателей.

Различают следующие типы факторного анализа:

• детерминированный (функциональный) и стохастический (корреляционный);

• прямой (дедуктивный) и обратный (индуктивный);

• одноступенчатый и многоступенчатый;

• статический и динамический;

• ретроспективный и перспективный (прогнозный).

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с резуль­тативным показателем носит функциональный характер, т.е. ре­зультативный показатель может быть представлен в виде произ­ведения, частного или алгебраической суммы факторов.

Стохастический факторный анализ представляет собой методику иссле­дования влияния факторов, связь которых с результативным показателем в отличие от функциональной является неполной, ве­роятностной (корреляционной). Если при функциональной зави­симости с изменением аргумента всегда происходит соответству­ющее изменение функции, то при корреляционной связи измене­ние аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих дан­ный показатель. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочета­ния других факторов, воздействующих на этот показатель.

При прямом факторном анализе исследование ведется дедук­тивным способом - от общего к частному. Обратный факторный анализ осуществляет исследование причинно-следственных свя­зей способом логичной индукции - от частных, отдельных факто­ров к обобщающим.

Факторный анализ может быть одноступенчатым и многоступенчатым. Первый тип используется для исследования факторов только одного уровня (одной ступени) подчинения без их детали­зации на составные части. Например, у = а - b. При многоступен­чатом факторном анализе проводится детализация факторов а и b на составные элементы с целью изучения их поведения. Дета­лизация факторов может быть продолжена дальше. В данном случае изучается влияние факторов различных уровней соподчиненности.

Статический анализ применяется при изучении влияния фак­торов на результативные показатели на соответствующую дату. Динамический анализ представляет собой методику исследования причинно-следственных связей в динамике.

Ретроспективный факторный анализ изучает причины изме­нения результативных показателей за прошлые периоды, а перс­пективный - исследует поведение факторов и результативных по­казателей в перспективе.

Основными задачами факторного анализа являются следую­щие:

· отбор факторов, которые определяют исследуемые результа­тивные показатели;

· классификация и систематизация факторов с целью обеспече­ния возможностей системного подхода;

· определение формы зависимости между факторами и: резуль­тативным показателем;

· моделирование взаимосвязей между результативными и фак­торными показателями;

· расчет влияния факторов и оценка роли каждого из них в из­менении величины результативного показателя;

· работа с факторной моделью, т.е. практическое ее использо­вание для управления экономическими процессами.

Отбор факторов для анализа того или другого показателя осу­ществляется на основе теоретических и практических знаний, при­обретенных в этой отрасли. При этом обычно исходят из принци­па: чем больше комплекс факторов исследуется, тем точнее будут результаты анализа.

Вместе с тем необходимо иметь в виду, что если этот комплекс факторов рассматривается как механическая сумма, без учета их взаимодействия, без выделения главных, оп­ределяющих, то выводы могут быть ошибочными. В экономичес­ком анализе взаимосвязанное исследование влияния факторов на величину результативных показателей достигается с помощью их систематизации.

2.

В детерминированном анализе для определения величины вли­яния отдельных факторов на изменение результативных показа­телей используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропор­ционального деления, интегральный и логарифмирования.

Простейшие детерминированные математические модели широко используются в анализе факторов производства. В практике анализа используют различные типы и виды моделей.

Аддитивные модели представляют собой алгебраическую сумму показателей и имеют следующий вид:

.

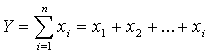К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях.

Мультипликативные модели в обобщенном виде могут быть представлены следующей формулой.

.

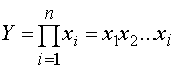Примером мультипликативной модели является двухфакторная модель объема реализации:

,

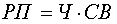где Ч – среднесписочная численность работников;

CB – средняя выработка на одного работника.

Кратные модели:

.

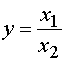Примером кратной модели служит показатель срока оборачиваемости товаров (в днях) - Т_ОБ.Т:

,

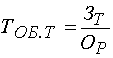где ЗТ – средний запас товаров;

ОР – однодневный объем реализации.

Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

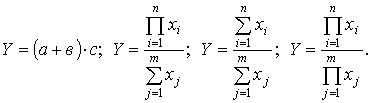
Примерами таких моделей служат показатели затрат на 1 руб. товарной продукции, показатели рентабельности и др.

Наиболее универсальным из сложных детерминированных моделей является способ цепной под­становки. Его сущность состоит в пос­ледовательном рассмотрении влияния отдельных факторов на общий результат. При этом последовательно заменяют базисные или плановые показатели фактическими и сравнивают новый ре­зультат, получаемый после замены, с прежним.

В общем виде применение способа цепных постановок можно описать следующим образом:

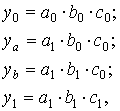
где a₀, b₀, c₀ – базисные значения факторов, оказывающих влияние на обобщающий показатель у;

a₁ , b₁, c₁ – фактические значения факторов;

y_a, y_b – промежуточные изменения результирующего показателя, связанного с изменением факторов а, b, соответственно.

Общее изменение ∆у=у₁–у₀ складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

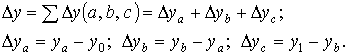
Способ абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:

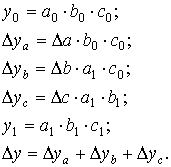
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида у = (а – в) х с. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.

Для мультипликативных моделей типа у = а х в х с методика анализа следующая:

- находят относительное отклонение каждого факторного показателя:

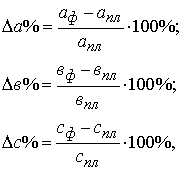
- определяют отклонение результативного показателя у за счет каждого фактора

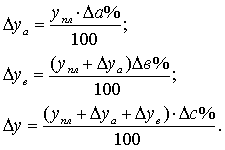
Метод цепных подстановок и способ абсолютных разниц име­ют общий недостаток, суть которого сводится к возникновению неразложимого остатка, который присоединяется к числовому значению влияния последнего фактора. В связи с этим величина влияния факторов на изменение ре­зультативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.

Чтобы избавиться от этого недостатка, в детерминированном факторном анализе в мультипликативных, кратных и смешанных моделях используется интегральный метод. Использование интег­рального метода позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов потому, что в данном случае результаты не зависят от местоположения факторов в мо­дели, а дополнительный прирост результативного показателя, который образуется от взаимодействия факторов, раскладывает­ся между ними пропорционально изолированному их воздействию на результативный показатель.

В ряде случаев для определения величины влияния факторов на прирост результативного показателя может быть использован способ пропорционального деления. Например, рентабельность ак­тивов снизилась на 5% в связи с увеличением активов предприя­тия на 200 тыс. руб. При этом стоимость внеоборотных активов возросла на 300 тыс. руб., а оборотных - уменьшилась на 100 тыс. руб. Значит, за счет первого фактора уровень рентабельности сни­зился, а за счет второго, повысился:

∆Р_осн = 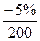*300 = -7,5%;

∆Р_об = 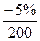*(-100) = +2,5%.

Индексный метод основывается на относительных показате­лях, выражающих отношение уровня данного явления к уровню его в прошлое время или к уровню аналогичного явления, приня­тому в качестве базы. Всякий индекс исчисляется соизмерением отчетной величины с базисной.

Классическая задача, решаемая с помощью индексного метода, - расчет влияния на объем продаж факторов количества и цен по схеме:

∑q₁p₁ - ∑q₀p₀ = (∑q₁p₀ - ∑q₀p₀) + (∑q₁p₁ - ∑q₁p₀),

где ∑q₁p₀ - ∑q₀p₀ – влияние количества;

∑q₁p₁ - ∑q₁p₀ – влияние цен.

Тогда индекс объема продаж (товарооборота), взятый в ценах соответствующих лет, имеет вид:

I_qp = .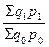

А индекс физического товарооборота:

I_q = .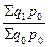

Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае резуль­таты расчета, как и при интегрировании, не зависят от места рас­положения факторов в модели и по сравнению с интегральным методом обеспечивается более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток в ограниченности сферы его при­менения.