Расчет амортизации имущества в EXCEL

EXCEL позволяет рассчитывать амортизацию имущества четырьмя способами:

1. Стандартный способ;

2. Метод постоянного учета амортизации;

3. Метод многократного учета амортизации;

4. Метод непосредственного учета амортизации.

Отличительно чертой всех четырех способов является то, что ни в одном из них норма амортизации не задается, а вычисляется на основе значений начальной и конечной (остаточной) стоимости имущества и периода эксплуатации. Это делается с помощью специальных функций. Все аргументы в этих функциях должны быть положительными числами.

Введем обозначение аргументов:

НС – начальная стоимость имущества;

ОС – остаточная стоимость имущества;

ВЭ – время эксплуатации имущества (лет, месяцев, дней);

П – период за который вычисляется амортизация ( имеет значение от 1 до ВЭ и измеряется в тех же единицах).

Остальные аргументы специфичны для различных функций.

Функция АМГД

Вычисляет величину амортизации имущества, используя стандартный метод расчета. Функция имеет формат:

АМГД(НС;ОС;ВЭ;П)

Стандартный учет амортизации предполагает следующую формулу расчета амортизации за конкретный период П:

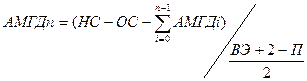
Т.е. амортизация считается, как некоторая доля от остаточной стоимости амортизации на данный период.

Пример: Начальная стоимость имущества – 100000 руб., остаточная стоимость – 10000 руб., срок эксплуатации – 5 лет. Вычислить стандартным способом амортизацию за каждый год.

Внесем данные в таблицу:

	А	В	С

Введем в ячейки с В2 по В6 формулы:

= АМГД(А1;В1;С1;А2), получим 30000 руб.

= АМГД(А1;В1;С1;А3), получим 24000 руб.

= АМГД(А1;В1;С1;А4), получим 18000 руб.

= АМГД(А1;В1;С1;А5), получим 12000 руб.

= АМГД(А1;В1;С1;А6), получим 6000 руб.

То есть:

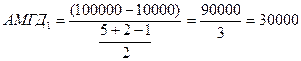
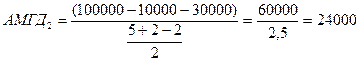
Фактически в 1-й период амортизация вычисляется исходя из нормы, равной (ВЭ +1)/2, а каждый последующий год числитель уменьшается на 0,5.

Сложив все полученные значения, получим 90000 руб.

Функция АМР

Вычисляет величину амортизации имущества за конкретный период, используя метод непосредственного учета. Функция имеет формат:

АМР(НС;ОС;ВЭ)

Непосредственная амортизация – это амортизация с фиксированной нормой амортизации, вычисляемая от стоимости амортизации (величины НС - ОС). Она постоянна каждый год и вычисляется по формуле:

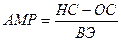
Пример: Начальная стоимость имущества 100000 руб., конечная – 10000 руб., срок эксплуатации 5 лет. Определить непосредственную амортизацию за каждый год.

Введем данные в таблицу:

	А	В	С	D

Введем в D1 формулу: = АМР(А1;В1;С1), получим 18000 руб.

То есть: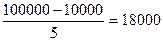

Проверим: 18000*5=90000 руб.

Функция ДДОБ

Вычисляет величину амортизации имущества за конкретный период, используя метод многократного учета. Метод многократного учета основан на использовании постоянной нормы амортизации, умноженной на остаточную стоимость имущества и предлагает ускоренную амортизацию от периода к периоду. Степень этого ускорения характеризуется специальным коэффициентом. Функция имеет формат:

ДДОБ_П= (НС;ОС;ВЭ;П;[К]),

где К – коэффициент, характеризующий степень ускорения амортизации; по умолчанию он равен 2 (метод двукратного учета амортизации). Амортизация при этом вычисляется по формуле:

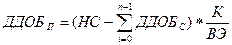
Если для какого-то года (чаще всего это бывает для последнего года) вычисленная амортизация превышает остаток амортизируемой стоимости, то амортизация равна этому остатку:

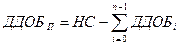, а в остальные годы равна 0.

Пример 1. Начальная стоимость имущества – 100000 руб., конечная – 10000 руб., срок эксплуатации – 5 лет. Найти амортизацию за каждый год методом двукратного учета.

Введем данные в таблицу:

	А	В	С

Введем следующие формулы в любые другие ячейки:

= ДДОБ(А1;В1;С1;1), получим 40000 руб.

= ДДОБ(А1;В1;С1;2), получим 24000 руб.

= ДДОБ(А1;В1;С1;3), получим 14400 руб.

= ДДОБ(А1;В1;С1;4), получим 8640 руб.

= ДДОБ(А1;В1;С1;5), получим 2960 руб.

То есть: ДДОБ₁=100000*2/5=40000

ДДОБ₂=(100000-40000)*2/5=24000

Для последнего периода должно бы получиться:

ДДОБ₅=(100000-40000-24000-14400-8640)*2/5=5184 руб.

Но в этом случае остаточная стоимость через 5 лет:

ОС=100000-40000-24000-14400-8640-5184=7776 руб.,

что меньше 10000, поэтому для этого периода

ДДОБ₅=100000-10000-40000-24000-14400-8640=2960 руб.

Пример 2. Начальная стоимость имущества – 100000 руб., конечная – 25000 руб., срок эксплуатации – 5 лет. Определить амортизацию за каждый год методом двукратного учета.

Введем в таблицу формулы:

= ДДОБ(100000;25000;5;1), получим 40000 руб.

= ДДОБ(100000;25000;5;2), получим 24000 руб.

= ДДОБ(100000;25000;5;3), получим 11000 руб.(хотя по формуле должно быть

14400)

= ДДОБ(100000;25000;5;4), получим 0.

= ДДОБ(100000;25000;5;5), получим 0.

Пример 3. Если для последнего периода (П=ВЭ) окажется, что остаточная стоимость не достигнута, то этот факт игнорируется, т.е. используется обычная формула. Пусть начальная стоимость – 100000 руб., остаточная стоимость – 100 руб., срок эксплуатации – 5 лет. Определить амортизацию за каждый год методом двукратного учета.

Введем в таблицу формулы:

= ДДОБ(100000;100;5;1), получим 40000 руб.

= ДДОБ(100000;100;5;2), получим 24000 руб.

= ДДОБ(100000;100;5;3), получим 14400 руб.

= ДДОБ(100000;100;5;4), получим 8640 руб.

= ДДОБ(100000;100;5;5), получим 5184 руб.

Остаточная стоимость имущества при этом:

ОС=100000-40000-24000-14400-8640-5184=7776 руб., а надо 100 руб., но это игнорируется.

Функция ДОБ

Вычисляет величину амортизации имущества за конкретный период, используя метод постоянного учета амортизации. Постоянная амортизация – это амортизация с постоянной процентной ставкой от остаточной стоимости имущества на данный период. Формула имеет формат:

ДОБ(НС;ОС;ВЭ;П;[М]),

где М – количество месяцев в первом году; если оно опущено, то по умолчанию принимается величина М=12.

Норма амортизации при этом вычисляется по формуле:

,

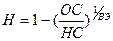а сама амортизация за период П:

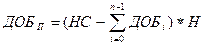
Если М¹12, то для первого и последнего периода используются особые формулы.

Пример. Начальная стоимость имущества – 100000 руб., конечная 10000 руб., срок эксплуатации – 5 лет. Определить амортизацию за каждый год методом постоянного учета.

Введем данные в таблицу:

	А	В	С

Введем в ячейки В2-В6 формулы:

= ДОБ(А1;В1;С1;А1), получим 36900,00 руб.

= ДОБ(А1;В1;С1;А2), получим 23283,90 руб.

= ДОБ(А1;В1;С1;А3), получим 14692,14 руб.

= ДОБ(А1;В1;С1;А4), получим 9270,74 руб.

= ДОБ(А1;В1;С1;А5), получим 5849,83 руб.

Для проверки вычислим процентную ставку:

За первый год: 36900/100000=0,369

За второй год: 23283,90/100000-36900=0,369 и т.д.

Функция ПДОБ

Вычисляет суммарную амортизацию за ряд периодов, используя метод многократного учета амортизации. Функция имеет формат:

ПДОБ(НС;ОС;ВЭ;НП;КП;[К;ПЕР], где

НП – начальный период, для которого вычисляется амортизация (лежит в диапазоне от 0 до ВЭ);

КП – конечный период (лежит в диапазоне от 0 до ВЭ, КП>НП);

К – коэффициент, имеющий тот же смысл, что и в функции ДДОБ;

ПЕР – логический переключатель, по умолчанию имеет значение ЛОЖЬ. Он имеет следующий смысл. Как видно из примера 3 на функцию ДДОБ, при данном методе не всегда достигается требуемая остаточная стоимость, чтобы избежать этого, если ПЕР имеет значение ЛОЖЬ, то данная функция переключается на режим непосредственного учета амортизации (по формуле АМР) за оставшийся период, если непосредственная амортизация больше многократной (по функции ДДОБ). Если ПЕР имеет значение ИСТИНА, то переключения не происходит (многократная амортизация вычисляется всегда).

Остаточная стоимость имущества при этом:

ОС=100000-40000-24000-14400-8640-5184=7776 руб., а надо 100 руб., но это игнорируется.

Пример1. Начальная стоимость имущества – 100000 руб., конечная – 10000 руб., срок эксплуатации – 5 лет. Определить суммарную амортизацию за первые два года.

Введем данные в таблицу:

	А	В	С	D	E	F

Введем в F1 формулу: = ПДОБ(А1;В1;С1;D1;Е1), получим 64000 руб.

Действительно, ДДОБ₁+ДДОБ₂= 40000+24000=64000 руб.

Пример2. Начальная стоимость имущества – 100000 руб., конечная – 10000 руб., срок эксплуатации – 5 лет. Найти суммарную амортизацию за 5 лет.

Введем данные в таблицу:

	А	В	С	D	E	F

Введем в F1 формулу: = ПДОБ(А1;В1;С1;D1;Е1), получим 99900 руб.

Действительно 100000-100=99900 руб.

Разберем эти расчеты.

Вычислим двукратную амортизацию за каждый год:

ДДОБ₁=40000 руб.

ДДОБ₂=24000 руб.

ДДОБ₃=14400 руб.

ДДОБ₄=8640 руб.

ДДОБ₅=5184 руб.

Сумма равна 92224 р., т.е. остаточная стоимость через 5 лет не достигается. Обозначим сумму амортизации за каждый год через А_i. Учитывая, что переключатель ПЕР по умолчанию имеет значение ЛОЖЬ, вычислим также непосредственную амортизацию.

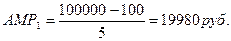
Т.к. ДДОБ₁>АМР₁, амортизация А₁=ДДОБ₁

За оставшиеся 4 года:

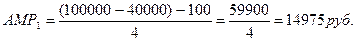
Т.к. ДДОБ₂>АМР₂, амортизация А₂=ДДОБ₂.

За оставшиеся 3 года:

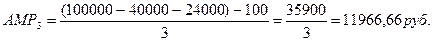
Т.К. ДДОБ₃>АМР₃, то амортизация А₃=ДДОБ₃.

За оставшиеся 2 года:

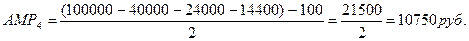
Т.к. ДДОБ₄<АМР₄, амортизация А₄=АМР₄ и соответственно

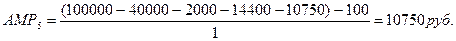
ДДОБ₅<АМР₅, то А₅=АМР₅

Итоговая сумма:

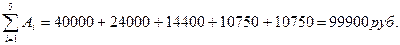
Пример3. В условиях примера 2 введем данные в F1 формулу:

=ПДОБ(А1;В1;С1;D1;Е1;2;1), получим 92224 руб.

Т.к. значение переключателя ПЕР=1(ИСТИНА), функция не переключается на равномерное непосредственное начисление амортизации.

Как видно из примера, если явно указывается значение переключателя ПЕР, то надо также явно указывать значение коэффициента К (даже если он равен 2).

Примечание.

В версии EXCEL XP и 2003 названия некоторых финансовых функций изменились. Эти изменения приведены в таблице:

Название функции в EXCEL 97 и 2000	Название функции в EXCEL XP и 2003
БЗ	БС
НПЗ	ЧПС
ПЗ	ПС
ВНДОХ	ВСД
НОРМА	СТАВКА
ОСНПЛАТ	ОСПЛТ
ПЛПРОЦ	ПРПЛТ
ППЛАТ	ПЛТ
АМГД	АСЧ
АМР	АПЛ
ПДОБ	ПУО

Задачи

Задача 1

Некто вложил 5 млн. рублей на 7 лет под 25% годовых, планируя ежегодно снимать по 350 тыс. рублей. Написать формулу для вычисления с помощью Excel, которая останется при этих условиях через 7 лет. Как проверить полученное решение с помощью обратной функции?

Задача 2

Банк выдал кредит в 10 млн. рублей под 40% годовых и рассчитывает получить в конце платежей утроенную сумму. Как с помощью Excel вычислить, на сколько лет он может выдать такой кредит (при условии возврата всех денег сразу, ежегодные платежи отсутствуют)?

Задача 3

Банк выдал кредит в 10 млн. рублей на три года под 35% годовых. Как с помощью Excel вычислить, какую сумму основного платежа получит банк за второй год?

Задача 4

Некто вложил деньги в акции компьютерной фирмы. В первый год было вложено 4 млн. руб., во второй – 5 млн. руб., в третий – 3 млн. руб. В первый год был получен доход 3,5, млн. руб., во второй и третий – по 4,5 млн. руб. Как с помощью Excel определить внутреннюю скорость оборота денег.

Задача 5

Некто положил 3,5 млн. руб. в банк под 25% годовых, планируя ежегодно снимать 1 млн. руб. Как с помощью Excel вычислить на сколько лет должно хватить этого вклада (т.е. через сколько лет на счету ничего не останется)?

Задача 6

Некто собирается взять через год кредит в 5 млн. руб. на 3 года с возвратом в первый год 1 млн. руб., во второй – 3 млн. руб. и в третий – 4 млн. руб. Деньги он собирается вложить в дело под 20% годовых. Как с помощью Excel определить, выгодно ли такое вложение?

Задача 7

Некто взял кредит в 3 млн. руб. под 30% годовых на пять лет. Написать формулу для вычисления с помощью Excel суммы основного платежа за кредит за третий год.

Задача 8

Некто вложил деньги в акции компьютерной фирмы. Для этого взят кредит в 4 млн. руб. под 20% годовых. В первой год акции принесли 5 млн. руб., во второй – 6 млн. руб. прибыль в обоих случаях была вложена в другие акции с доходностью 15% годовых. Как с помощью Excel определить внутреннюю скорость оборота денег?

Задача 9

Некто взял в банке кредит в 5 млн. руб. под 35% годовых, рассчитывая через несколько лет получить прибыль, из которой вернуть банку 15 млн. руб. Как с помощью Excel определить, на сколько лет банк может выдать такой кредит (при условии возврата всех денег сразу, ежегодные платежи отсутствуют)?

Задача 10

Банк выдал кредит в 15 млн. руб. на 10 лет, рассчитывая без промежуточных платежей в итоге получить утроенную сумму. Как с помощью Excel определить, какую процентную ставку он должен установить?

Задача 11

Некто собирается взять в начале года кредит в 5 млн. руб. на три года с возвратом в первый год 1 млн. руб., во второй – 3 млн. руб., и в третий – 4 млн. руб. Деньги он собирается вложить в дело под 20% годовых. Как с помощью Excel определить, выгодно ли такое вложение?

Задача 12

Некто взял в банке ссуду в 15 млн. руб. на 5 лет под 20% годовых. Написать формулу вычисления с помощью Excel суммы ежегодных выплат по ссуде.

Задача 13

Некто сделал вклад в 3 млн. руб. на 4 года, планируя в течение этого срока не делать никаких снятий, а в конце срока получить 10 млн. руб. Как с помощью Excel определить, под какой процент он должен положить деньги?

Задача 14

Некто собирается взять через год кредит в 5 млн. руб. на 3 года с возвратом в первый год 1 млн. руб., во второй – 2 млн. руб. и в третий – 4 млн. руб. Деньги он собирается вложить в дело под 20% годовых. Как с помощью Excel определить, выгодно ли такое вложение?

Задача 15

Некто взял в банке ссуду в 15 млн. руб. на 5 лет под 20% годовых. Написать формулу вычисления с помощью Excel платы по процентам за первый, второй и третий год.

Задача 16

Как с помощью Excel определить, сколько денег окажется на счету, если каждый год в течение пяти лет вкладывать по 1 млн. руб. при условии, что банк гарантирует доход 15%? Как проверить это решение с помощью обратной функции?

Задача 17

Некто собирается взять в начале года кредит в 5 млн. руб. на три года с возвратом в первый год 1 млн. руб., во второй – 2 млн. руб. и в третий – 4 млн. руб. Деньги он собирается вложить в дело под 20% годовых. Как с помощью Excel определить, выгодно ли такое вложение?

Задача 18

Банк принимает вклады в 10 млн. руб. на 5 лет с правом ежегодного снятия клиентом по 1 млн. руб. Как с помощью Excel определить, какую процентную ставку он должен установить, чтобы в конце срока выплатить сумму в 25 млн. руб.?

Задача 19

Некто хочет сделать заем в конце года из расчета 15% годовых с ежегодной выплатой 2млн. руб., погашение которого гарантируется в течение 5 лет. Как с помощью Excel определить, на какую сумму можно сделать такой заем? Как проверить решение с помощью обратной функции?

Задача 20

Некто собирается в начале года вложить деньги в предприятие стоимостью 50 млн. руб., рассчитывая получить в первый год доход в 15 млн. руб., во второй – 30 млн. руб., в третий – 40 млн. руб. Как с помощью Excel определить, выгодно ли такое вложение, если степень инфляции – 8%?

Задача 21

Некто взял ссуду в 10 млн. руб. на 2 года под 40% годовых. Как с помощью Excel определить общую плату за кредит и сумму основного платежа и платы по процентам за каждый год? Чему должна быть равна сумма основного платежа и платы по процентам за каждый год?

Задача 22

Некто собирается в конце года вложить деньги в предприятие стоимостью 50 млн. руб., рассчитывая получить в первый год доход в 15 млн. руб., во второй – 30 млн. руб., в третий – 40 млн. руб. Как с помощью Excel определить, выгодно ли такое вложение, если степень инфляции – 8%?

Задачи 23 – 31

Найти величину амортизации имущества за каждый год следующими способами:

- стандартного учета амортизации;

- постоянного учета амортизации;

- непосредственного учета амортизации;

- двукратного учета амортизации.

Сравнить полученные результаты.

По результатам расчета амортизации стандартным способом построить диаграмму, отражающую зависимость величины амортизации от времени (т.е. по годам). Тип диаграммы выбрать по своему желанию.

К задаче 23

Начальная стоимость некоторого имущества составляет 1 млн. руб., конечная стоимость – 150 тыс. руб., срок эксплуатации – 6 лет.

К задаче 24

Начальная стоимость некоторого имущества составляет 1,2 млн. руб., конечная стоимость – 250 тыс. руб., срок эксплуатации – 6 лет.

К задаче 25

Начальная стоимость некоторого имущества составляет 3 млн. руб., конечная стоимость – 150 тыс. руб., срок эксплуатации – 6 лет.

К задаче 26

Начальная стоимость некоторого имущества составляет 2,7 млн. руб., конечная стоимость – 0,8 млн. руб., срок эксплуатации – 6 лет.

К задаче 27

Начальная стоимость некоторого имущества составляет 8,8 млн. руб., конечная стоимость – 1 млн. руб., срок эксплуатации – 6 лет.

К задаче 28

Начальная стоимость некоторого имущества составляет 11 млн. руб., конечная стоимость – 1,4 млн. руб., срок эксплуатации – 6 лет.

К задаче 29

Начальная стоимость некоторого имущества составляет 4,7 млн. руб., конечная стоимость – 500 тыс. руб., срок эксплуатации – 6 лет.

К задаче 30

Начальная стоимость некоторого имущества составляет 5,3 млн. руб., конечная стоимость – 400 тыс. руб., срок эксплуатации – 6 лет.

К задаче 31

Начальная стоимость некоторого имущества составляет 6,4 млн. руб., конечная стоимость – 1,5 млн. руб., срок эксплуатации – 6 лет.