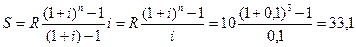Номинальная и эффективная учетные ставки процентов

Номинальная учетная ставка. В тех случаях, когда дисконтирование применяют m раз в году, используют номинальную учетную ставкуf. Тогда в каждом периоде, равном 1/m части года, дисконтирование осуществляется по сложной учетной ставке f/m. Процесс дисконтирования по этой сложной учетной m раз в году описывается формулой

P=S(1-f/m)^N, (3.10)

где N - общее число периодов дисконтирования (N=mn).

Дисконтирование не один, а m раз в году быстрее снижает величину дисконта.

Эффективная учетная ставка. Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную (по финансовым результатам) номинальной, применяемой при заданном числе дисконтирований в году m.

соответствии с определением эффективной учетной ставки найдем ее связь с номинальной из равенства дисконтных множителей

(1-f/m)^mn=(1-d_сл)ⁿ,

из которого следует, что

d_сл=1-(1-f/m)^m. (3.11)

Отметим, что эффективная учетная ставка всегда меньше номинальной.

Наращение по сложной учетной ставке.Наращение является обратной задачей для учетных ставок. Формулы наращения по сложным учетным ставкам можно получить, разрешая соответствующие формулы для дисконтирования (38 и 3.10) относительно S. Получаем

Из P=S(1-d_сл)ⁿ

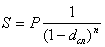, (3.12)

а из P=S(1-f/m)^N

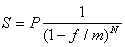. (3.13)

Пример.Какую сумму следует проставить в векселе, если реально выданная сумма равна 20 млн. руб., срок погашения 2 года. Вексель рассчитывается, исходя из сложной годовой учетной ставки 10%.

Решение.

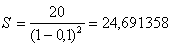млн. руб.

Пример.

Решить предыдущую задачу при условии, что наращение по сложной учетной ставке осуществляется не один, а 4 раза в год.

Решение.

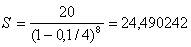млн. руб.

Непрерывные проценты

2.3.1. Наращение и дисконтирование. Наращенная сумма при дис­кретных процентах определяется по формуле

S=P(1+j/m)^mn,

где j - номинальная ставка процентов,

m - число периодов начисления процентов в году.

Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m®¥ имеем

S = lim P(1 + j/m)^mn = P lim[(1 + j/m)^m]ⁿ (2.23)

m®¥ m®¥

Используя известный из математического анализа второй замеча­тельный предел, можно записать

lim(1 + j/m)^m = lim[(1 + j/m)^m/j]^j = e^j, (2.23)

m®¥ m®¥

где e - основание натуральных логарифмов.

Подставляя полученное выражение в формулу (2.23), окончательно получаем, что наращенная сумма в случае непрерывного начисления про­центов по ставке j равна

S=Pe^{j n}. (2.24)

Для того чтобы отличать ставку непрерывных процентов от ставок дис­кретных процентов, ее называют силой роста и обозначают символом δ. С учетом введенного обозначения равенство (2.24) принимает вид

S=Pe ^{δ n}. (2.25)

Сила роста δ представляет собой номинальную ставку процентов при m→∞.

Дисконтирование на основе непрерывных процентных ставок осу­ществляется по формуле

P=Se ^{-δ n}. (2.26)

2.3.2. Связь дискретных и непрерывных процентных ставок. Дис­кретные и непрерывные процентные ставки находятся в функциональной зависимости, благодаря которой можно осуществлять переход от расчета непрерывных процентов к дискретным и наоборот. Формулу эквивалент­ного перехода от одних ставок к другим можно получить, приравнивая со­ответствующие множители наращения

(1+i)ⁿ=e ^δn. (2.27)

Из записанного равенства следует, что

δ =ln(1+i), (2.28)

i=e^δ -1. (2.29)

Пример 2.13. Годовая ставка сложных процентов равна 15%. Чему равна эквивалентная сила роста?

Решение. Воспользуемся формулой (2.28)

δ =ln(1+i)=ln(1+0,15)=0,13976, т.е. эквивалентная сила роста равна 13,976%.

2.3.3. Расчет срока ссуды и процентных ставок В ряде практических задач начальная (P) и конечная (S) суммы зада­ны контрактом, и требуется определить либо срок платежа, либо процент­ную ставку, которая в данном случае может служить мерой сравнения с рыночными показателями и характеристикой доходности операции для кредитора. Указанные величины нетрудно найти из исходных формул на­ращения или дисконтирования. По сути дела, в обоих случаях решается в известном смысле обратная задача.

Срок ссуды. А) При наращивании по сложной годовой ставке i.

Из исходной формулы наращения S=P(1+i)ⁿ следует, что

n = log(S/P) / log(1 + i) (2.30)

где логарифм можно взять по любому основанию, поскольку он имеется как в числителе, так и в знаменателе.

Б) При наращивании по номинальной ставке процентов m раз в году из формулы: S=P(1+j/m)^mn получаем:

n = log(S / P) / mlog(l + j/m) (2.31)

В) При дисконтировании по сложной годовой учетной ставке d.

Из формулы P=S(1-d)ⁿ имеем

n = log(P/S) / log (l - d) (2.32)

Г) При дисконтировании по номинальной учетной ставке m раз в году. Используя равенство P=S(1-f/m)^mn, приходим к формуле:

n = log(P/S) / mlog(1-f/m) (2.33)

Д) При наращивании по постоянной силе роста. Исходя из S=Pe^δn

получаем:

ln(S/P)=δn. (2.34)

Расчет процентных ставок. Из тех же исходных формул, что и вы­ше, получим выражения для процентных ставок.

А) При наращивании по сложной годовой ставке i. Из исходной формулы наращения S=P(1+i)ⁿ следует, что

(2.35)

Б) При наращивании по номинальной ставке процентов m раз в году из формулы S=P(1+j/m)^mn, получаем:

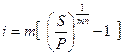(2.36)

В) При дисконтировании по сложной годовой учетной ставке d. Из формулы P=S(1-d)ⁿ имеем

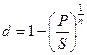(2.37)

Г) При дисконтировании по номинальной учетной ставке m раз в го­ду. Из P=S(1-f/m)^mn приходим к формуле:

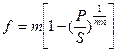(2.38)

Д) При наращивании по постоянной силе роста. Исходя из

S=Pe^δn,

Получаем

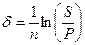(2.39)

2.4. Начисление процентов в условиях инфляции и налогообложения

Следствием инфляции является падение покупательной способности денег, которое за период n характеризуется индексом J_n. Индекс покупа­тельной способности равен обратной величине индекса цен J_p, т.е.

Jn=1/J_p. (2.40)

Напомним, что индекс цен показывает во сколько раз выросли цены за рассматриваемый промежуток времени.

2.4.1. Наращение по простым процентам. Если наращенная за n лет сумма денег составляет S, а индекс цен равен J_p, то реально наращен­ная сумма денег, с учетом их покупательной способности, равна

C=S/J_P. (2.41)

Пусть ожидаемый средний годовой темп инфляции (характеризую­щий прирост цен за год) равен h. Тогда годовой индекс цен составит (1 +h).

Если наращение производится по простой ставке в течение n лет, то реальное наращение при темпе инфляции h составит:

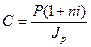(2.42)

где в общем случае

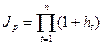(2.43)

и, в частности, при неизменном темпе роста цен h

Jp=(1+h)ⁿ. (2.44)

Процентная ставка, которая при начислении простых процентов компенсирует инфляцию, равна

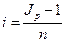--------------------------------------- (2.45)

Один из способов компенсации обесценения денег заключается в увеличении ставки процентов на величину так называемой инфляционной премии. Скорректированная таким образом ставка называется брутто- ставкой. Брутто-ставка, которую мы будем обозначать символом r, нахо­дится из равенства скорректированного на инфляцию множителя нараще­ния по брутто-ставке множителю наращения по реальной ставке процента

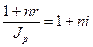(2.46)

откуда

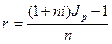(2.47)

2.4.2. Наращение по сложным процентам. Наращенная по слож­ным процентам сумма к концу срока ссуды с учетом падения покупатель­ной способности денег (т.е. в неизменных рублях) составит

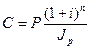(2.48)

где индекс цен определяется выражением (2.43) или (2.44), в зависи­мости от непостоянства или постоянства темпа инфляции.

В этом случае падение покупательной способности денег компенсируется при ставке i = h, C=P.

Применяются два способа компенсации потерь от снижения покупа­тельной способности денег при начислении сложных процентов.

А) Корректировка ставки процентов, по которой производится нара­щение, на величину инфляционной премии. Ставка процентов, увеличен­ная на величину инфляционной премии, называется брутто-ставкой. Будем обозначать ее символом r. Считая, что годовой темп инфляции равен h, можем написать равенство соответствующих множителей наращения

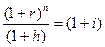(2.49)

где i - реальная ставка.

Отсюда

r=i+h+ih. (2.50)

То есть инфляционная премия равна h+ih.

Б) Индексация первоначальной суммы P. В этом случае сумма P корректируется согласно движению заранее оговоренного индекса. Тогда

S=PJ_p(1+i)ⁿ. (2.51)

Нетрудно заметить, что и в случае А) и в случае Б) в итоге мы при­ходим к одной и той же формуле наращения (2.51). В ней первые два со­множителя в правой части отражают индексацию первоначальной суммы, а последние два - корректировку ставки процента.

2.4.3. Измерение реальной ставки процента. На практике прихо­дится решать и обратную задачу - находить реальную ставку процента в условиях инфляции. Из тех же соотношений между множителями нараще­ния нетрудно вывести формулы, определяющие реальную ставку i по за­данной (или объявленной) брутто-ставке r.

При начислении простых процентов годовая реальная ставка про­центов равна

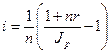(2.52)

При начислении сложных процентов реальная ставка процентов оп­ределяется следующим выражением

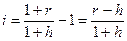(2.53)

2.4.4. Учет налогов. В ряде стран проценты, получаемые кредито­ром или вкладчиком, облагаются налогом. Это, конечно, уменьшает вели­чину реально получаемой наращенной суммы. Расчет этой суммы можно представить следующим образом.

Обозначим наращенную сумму до уплаты налогов, как и раньше, че­рез S, а после уплаты через C. Пусть ставка налога равна g.

Тогда при начислении простых процентов получаем, что сумма на­лога равна Ig = (S-P)g, а наращенная сумма после уплаты налогов

C = S-(S-P)g = S(1-g)+Pg = P[1+n(1-g)i]. (2.54)

Это выражение означает, что при начислении простых процентов учет на­лога сводится к соответствующему сокращению процентной ставки: для получения реального наращения следует вместо ставки i применять ставку (1-g)i.

При начислении налога на сложные проценты, применяемые обыч­но в среднесрочных и долгосрочных операциях, возможны два варианта расчета: определение налога за весь срок сразу или расчет процентов за каждый год в отдельности. Первый вариант удобен, когда налоговая ставка в пределах облагаемого налогом периода, остается неизменной. Второй оказывается единственно возможным, когда налоговая ставка из года в год меняется.

В первом варианте расчета сумма налога за весь срок равна

(S-P)g=P [(1+i)ⁿ-1]g, (2.55)

а наращенная сумма после выплаты налога рассчитывается по формуле

C = S-(S-P)g = S(1-g)+Pg = P[(1-g)(1+i)ⁿ+g]. (2.56)

Во втором варианте сумма налога рассчитывается за каждый истекший год. Поскольку речь идет о сложных процентах, ясно, что сумма про­центов будет из года в год возрастать, соответственно будет изменяться и сумма налога.

Обозначим сумму налога за год t через G_t. Ее можно найти с помо­щью следующего рекуррентного соотношения

G_t=I_tg=(S_t-S_t-1)g=P[(1+i)^t-(1+i)^t-1]g. (2.57)

Если налоговая ставка постоянна, то сумма налогов за весь срок, рассчитанная первым способом, равна сумме налогов, рассчитанных за со­ответствующие годы вторым способом.

2.5. Потоки платежей

Очень часто в контрактах финансового характера предусматривают­ся не отдельные разовые платежи, а серию платежей, распределенных во времени. Примерами могут быть регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами, пе­риодические взносы на расчетный счет, на котором формируется некото­рый фонд различного назначения (инвестиционный, пенсионный, страхо­вой, резервный, накопительный и т.д.), дивиденды, выплачиваемые по ценным бумагам, выплаты пенсий из пенсионного фонда и пр. Ряд после­довательных выплат и поступлений называют потоком платежей. Выпла­ты представляются отрицательными величинами, а поступления - положи­тельными.

Обобщающими характеристиками потока платежей являются нара­щенная сумма и современная величина. Каждая из этих характеристик яв­ляется числом.

Наращенная сумма потока платежей это сумма всех членов по­следовательности платежей с начисленными на них процентами к концу срока ренты.

Под современной величиной потока платежей понимают сумму всех его членов, дисконтированных (приведенных) на некоторый момент времени, совпадающий с началом потока платежей или предшествующий ему.

Конкретный смысл этих обобщающих характеристик определяется природой потока платежей, причиной, его порождающей. Например, на­ращенная сумма может представлять собой итоговый размер формируемо­го инвестиционного или какого-либо другого фонда, общую сумму задол­женности. Современная величина может характеризовать приведенную прибыль, приведенные издержки.

2.5.1. Финансовые ренты и их классификация. Поток платежей, все члены которого положительные величины, а временные интервалы по­стоянны, называют финансовой рентой или аннуитетом.

Финансовая рента имеет следующие параметры: член ренты - вели­чина каждого отдельного платежа, период ренты - временной интервал между двумя соседними платежами, срок ренты - время, измеренное от начала финансовой ренты до конца ее последнего периода, процентная ставка - ставка, используемая при наращении или дисконтировании пла­тежей, образующих ренту.

Виды финансовых рент. Классификация рент может быть произве­дена по различным признаками. Рассмотрим их.

В зависимости от продолжительности периода, ренты делят на годо­вые и p-срочные, где p - число выплат в году.

По числу начислений процентов различают ренты с начислением один в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей.

По величине членов различают постоянные (с равными членами) и переменные ренты. Если размеры платежей изменяются по какому-либо математическому закону, то часто появляется возможность вывести стан­дартные формулы, значительно упрощающие расчеты.

По вероятности выплаты членов различают ренты верные и услов­ные. Верные ренты подлежат безусловной выплате, например, при пога­шении кредита. Выплата условной ренты ставится в зависимость от насту­пления некоторого случайного события. Поэтому число ее членов заранее неизвестно. Например, число выплат пенсий зависит от продолжительно­сти жизни пенсионера.

По числу членов различают ренты с конечным числом членов, или ограниченные, и бесконечные, или вечные. В качестве вечной ренты вы­ступают, например, выплаты по облигационным займам с неограниченны­ми или не фиксированными сроками.

В зависимости от наличия сдвига момента начала ренты по отноше­нию к началу действия контракта или какому-либо другому моменту вре­мени ренты подразделяются на немедленные и отложенные, или отсро­ченные. Срок немедленных рент начинается сразу, а у отложенных запаз­дывает.

Ренты различают по моменту выплаты платежей. Если платежи осу­ществляются в конце каждого периода, то такие ренты называются обыч­ными или постнумерандо. Если же выплаты производятся в начале каж­дого периода, то ренты называются пренумерандо. Иногда предусматри­ваются платежи в середине каждого периода.

Анализ потоков платежей в большинстве случаев предполагает рас­чет наращенной суммы или современной величины ренты.

2.5.2. Формулы наращенной суммы. Обычная годовая рента.

Пусть в конце каждого года в течение n лет на расчетный счет вносится по R рублей, сложные проценты начисляются один раз в год по ставке i. В этом случае первый взнос к концу срока ренты возрастет до величины R(1+i)^n-1, так как на сумму R проценты начислялись в течение n-1 года. Второй взнос увеличится до R(1+i)^n-2 и т.д. На последний взнос проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометрической прогрессии S=R+R(1+i)+R(1+i)²+…….+R(1+i)^n-1,

в которой первый член равен R, знаменатель (1+i), число членов n. Как из­вестно из курса школьной алгебры, эта сумма равна

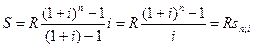(2.58)

где

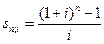(2.59)

называется коэффициентом наращения ренты. Он зависит только от срока ренты n и уровня процентной ставки i. Поэтому его значения могут быть представлены в таблице с двумя входами.

Пример. В течение 3 лет на расчетный счет в конце каждого го­да поступает по 10 млн. руб., на которые 1 раз в год начисляются процен­ты по сложной годовой ставке 10%. Требуется определить сумму на рас­четном счете к концу указанного срока.

Решение. По формуле (2.58) находим