Основные термины и понятия
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Кузбасский государственный технический университет»
Кафедра вычислительной техники и информационных технологий
ОСНОВЫ РАБОТЫ В MS EXCEL 2007
Часть 2
Методические указания к лабораторным работам
по дисциплине «Информатика» для студентов специальности
080502 – "Экономика и управление на предприятии"
| Составитель | Е.В. Прокопенко |
| Утверждены на заседании кафедры Протокол № __ от "__" "_______" 2010г | |||
| Рекомендованы к печати учебно-методической комиссией специальности 080502 Протокол № ___ от "__" "_________" 2010г Электронная копия хранится в библиотеке ГУ КузГТУ | |||
КЕМЕРОВО 2010
Содержание
Введение. 2
Цель работ. 2
Запуск MS Excel 2007. 2
Основные термины и понятия. 2
ЛАБОРАТОРНАЯ РАБОТА № 1. 5
ЛАБОРАТОРНАЯ РАБОТА № 2. 7
ЛАБОРАТОРНАЯ РАБОТА № 3. 8
ЛАБОРАТОРНАЯ РАБОТА № 4. 9
ЛАБОРАТОРНАЯ РАБОТА № 5. 11
ЛАБОРАТОРНАЯ РАБОТА № 6. 13
ЛАБОРАТОРНАЯ РАБОТА № 7. 16
Приложение 1. Список финансовых функций MS EXCEL. 23
Список рекомендуемой литературы.. 27
Интернет-ресурсы.. 27
Введение
Методические указания к лабораторным работам по дисциплине «Информатика» часть 2 содержат сведения, необходимые для выполнения лабораторных работ по темам: "Использование финансовых функций MS Excel для расчета по займам и кредитам", " Решение систем линейных алгебраических уравнений средствами MS Excel". Количество часов – 4, количество лабораторных работ – 7.
Цель работ
Целью лабораторных работ является изучение практических навыков и основных принципов работы в программе, а именно:
Uuml; Изучение возможностей пакета MS Excel при решении финансовых задач. Приобретение навыков решения финансовых задач, расчетов по займам и кредитам.
Uuml; Изучение возможностей пакета MS Excel при решении задач линейной алгебры. Приобретение навыков решения систем линейных алгебраических уравнений и выполнение действий над матрицами средствами пакета.
Запуск MS Excel 2007
Запуск MS Excel осуществляется посредством выбора на рабочем столе ярлыка программы или с помощью кнопки Пуск→
Все программы → Microsoft Office → MS Excel.
При запуске MS Excel на экране появляется рабочая книга
Книга1, содержащая несколько рабочих листов. Каждый лист представляет собой таблицу, состоящую из строк и столбцов. В этих таблицах хранятся данные.
Основные термины и понятия
Количественный финансовый анализ предполагает применение унифицированных моделей и методов расчета финансовых показателей.
Условно методы финансовой математики делятся на две категории:
базовые и прикладные. К базовым методам и моделям относятся:
1) простые и сложные проценты как основа операций, связанных с наращением или дисконтированием платежей;
2) расчет последовательностей (потоков) платежей применительно к различным видам финансовых рент.
К прикладным методам финансовых расчетов относятся:
1) планирование и оценка эффективности финансово-кредитных операций;
2) расчет страховых аннуитетов;
3) планирование погашения долгосрочной задолженности;
4) планирование погашения ипотечных ссуд и потребительских кредитов;
5) финансовые расчеты по ценным бумагам;
6) лизинговые, факторинговые и форфейтинговые банковские операции;
7) планирование и анализ инвестиционных проектов и др.
Особенностью всех финансовых расчетов является временная ценность денег, то есть принцип неравноценности денег, относящихся к разныммоментам времени. Предполагается, что полученная сегодня сумма обладаетбольшей ценностью, чем ее эквивалент, полученный в будущем, то естьбудущие поступления менее ценны, чем современные. Неравноценностьодинаковых по абсолютной величине сумм связана прежде всего с тем, чтоимеющиеся сегодня деньги могут быть инвестированы и принести доход вбудущем.
Основными понятиями финансовых методов расчета являются:
процент – абсолютная величина дохода от предоставления денег в долг в любой его форме;
процентная ставка – относительная величина дохода за фиксированный интервал времени, измеряемая в процентах или в виде дроби;
период начисления – интервал времени, к которому приурочена процентная ставка;
капитализация процентов – присоединение начисленных процентов к основной сумме;
наращение – увеличение первоначальной суммы в связи с капитализацией;
дисконтирование – приведение стоимостной величины, относящейся к будущему, на некоторый, обычно более ранний момент времени (операция, обратная наращению).
В финансовых расчетах используются следующие виды процентных ставок:
• в зависимости от базы для начисления процентов различают простые проценты (постоянная база) и сложные проценты (переменная база);
• по принципу расчета различают ставку наращения – декурсивная ставка и учетную ставку – антисипативнал ставка;
• по постоянству значения процентной ставки в течение действия контракта – фиксированные и плавающие (фиксируется ли изменяющаяся во времени база и размер надбавки к ней – маржи).
Существуют различные способы начисления процентов от предоставления денег в долг в любой форме. Соответственно применяют разные виды процентных ставок.
Проценты различаются по базе их начисления. Применяется постоянная и последовательно изменяющаяся база для расчета. В последнем случае за базу принимается сумма, полученная на предыдущем этапе наращения или дисконтирования.
При постоянной базе используют простые проценты, при переменной – сложные процентные ставки.
ЛАБОРАТОРНАЯ РАБОТА № 1
Задача:
Фирма создает фонд для погашения долгосрочных обязательств, для чегоперечисляет ежегодно в течение 4 лет платежи размером 200тыс.р. В конце каждого года, на которые начисляются сложные проценты по ставке 25% годовых, начисляемых ежеквартально. Определить величину фонда к концувыплат.
Технология работы:
Для решения данной задачи необходимо выполнить следующие действия:
1. Вызвать мастер функций.
2. Из общего списка выбрать функцию БС.
3. Заполнить диалоговое окно, то есть внести необходимые аргументы функции (в поля ввода можно вводить как ссылки на ячейки, содержащие значения аргументов, так и сами значения), рис.1.
4. Завершить ввод аргументов и запуск расчета значений функции нажатием – кнопки ОК.
5. При отказе работы с функцией нажать кнопку Отмена.
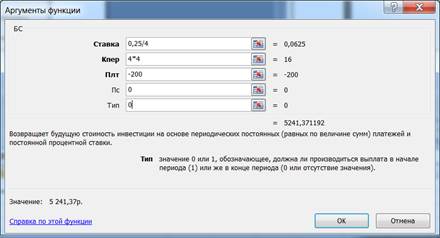
Рис. 1. Диалоговое окно ввода аргументов функции БС.
Краткие комментарии по значениям аргументов функции БС:
• величина периодических выплат (поле Выплата), согласно правилам заполнения должна быть введена со знаком минус;
• по условию задачи мы соответствующим образом скорректировали поля Норма и Число периодов, так как предусматривается ежеквартальное начисление процентов.
• значение 0 у параметра Тип принимается по умолчанию и означает, что применяется аннуитетпостнумерандо(взносы в конце года), значение –1 означает аннуитетапренумерандо (взносы в начале года).
Параллельно процессу заполнения полей аргументов происходит формирование результата расчетов, окончательно он равен 2271,93.Для завершения ввода функции БЗ в ячейку рабочего листа MS Excel следует нажать кнопку ОК. Читателю в качестве упражнения предлагается проверить самостоятельно, что в случае аннуитета пренумерандо результат был бы равен 5241,37.
Врезультате ячейка будет содержать формулу:
=БЗ(0,25/4*4;-4;-200;;0)
Ответ: 5241,37.
ЛАБОРАТОРНАЯ РАБОТА № 2
Задача:
Банк выдает долгосрочный кредит в размере 2000 тыс. р. по сложной ставке 15% годовых. Определить сумму долга через 10 лет.
Технология работы:
Для решения данной задачи необходимо выполнить следующие действия:
1. Вызвать мастер функций.
2. Из общего списка выбрать функцию БС.
3. Заполнить диалоговое окно, то есть внести необходимые аргументы функции (в поля ввода можно вводить как ссылки на ячейки, содержащие значения аргументов, так и сами значения), рис.2.
4. Завершить ввод аргументов и запуск расчета значений функции нажатием – кнопки ОК.
5. При отказе работы с функцией нажать кнопку Отмена.
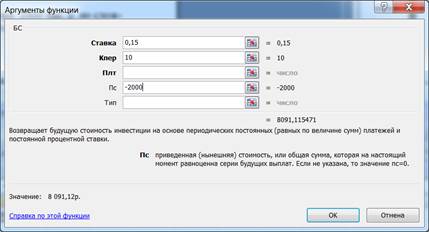
Рис.2. Диалоговое окно ввода аргументов функции БС.
Необходимо правильнозаполнить поля ввода функции БС. Для решения этой задачи нужно заполнить не поле Выплата, а поле ПС, так как в этом случае финансовая функция будет рассчитывать значение FV просто по формуле нахождения будущей стоимости дли сложных процентов:
FV=PV(1+i)".
Заполним финансовую функцию БС следующим образом: =БЗ(0,15;10;;-2000).
Ответ: 8091,12.
ЛАБОРАТОРНАЯ РАБОТА № 3
Задача:
Платежи в фонд будут вноситься ежегодно по 350 тыс.р. в течение 7 лет с начислением па них сложных процентов по ставке 12% годовых. Определить современную сумму всех платежей с начисленными процентами.
Технология работы:
Для решения данной задачи необходимо выполнить следующие действия:
1. Вызвать мастер функций.
2. Из общего списка выбрать функцию ПС.
3. Заполнить диалоговое окно, то есть внести необходимые аргументы функции (в поля ввода можно вводить как ссылки на ячейки, содержащие значения аргументов, так и сами значения), рис.3.
4. Завершить ввод аргументов и запуск расчета значений функции нажатием – кнопки ОК.
5. При отказе работы с функцией нажать кнопку Отмена.
Для решения следует использовать функцию
=ПС(норма:0,12; число периодов:7; выплата:-350;; тип:0).
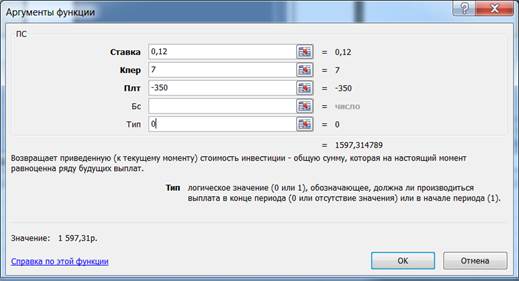
Рис.3. Диалоговое окно ввода аргументов функции ПС.
Ответ: 1597,31.
ЛАБОРАТОРНАЯ РАБОТА № 4
Задача:
Инвестиции в проект составляют 700тыс.р. В последующие 4 года ожидаются следующие годовые доходы по проекту: 150; 250; 300; 450тыс.р. Издержки привлечения капитала 5%. Рассчитать чистую текущую стоимость проекта.
Технология работы:
Для решения данной задачи необходимо выполнить следующие действия:
1. Вызвать мастер функций.
2. Из общего списка выбрать функцию ЧПС.
3. Заполнить диалоговое окно, то есть внести необходимые аргументы функции (в поля ввода можно вводить как ссылки на ячейки, содержащие значения аргументов, так и сами значения), рис.4.
4. Завершить ввод аргументов и запуск расчета значений функции нажатием – кнопки ОК.
5. При отказе работы с функцией нажать кнопку Отмена.
Для решения следует использовать функцию
=ЧПС(норма: 0,05; значения: — диапазон ячеек со значениями доходов по проекту).
Для нахождения непосредственного значения NPV необходимо вычесть начальную инвестицию.
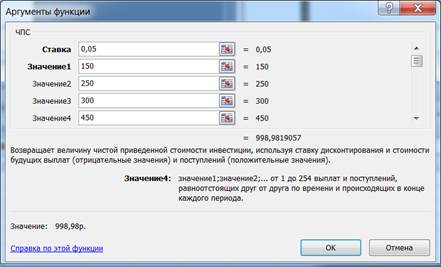
Рис.4. Диалоговое окно ввода аргументов функции ЧПС.
Для нахождения непосредственного значения NPV необходимо вычесть начальную инвестицию: 998,98-700=298,98.
Следует заметить, что положительное значение NPV является показателем того, что проект приносит чистую прибыль своим инвесторам после покрытия всех связанных с ним расходов.
Ответ: 298,98.
ЛАБОРАТОРНАЯ РАБОТА № 5
Задача:
Инвестиции в проект составляют 700 тыс.р. В последующие 4 года ожидаются следующие годовые доходы по проекту: 150; 250; 300; 450 тыс.р. Издержки привлечения капитала 5%. Рассчитать чистую текущую стоимость проекта.
Заданы конкретные даты: выплата – 1.01.11г., поступления –2.02.11г., 15.03.11г., 25.03.11г., 10.04.11г. соответственно.
Технология работы:
Для решения данной задачи необходимо выполнить следующие действия:
1. В ячейки А2:А6 денежные значения. В ячейки В2:В6 ввести значения даты. В С2 значение процентной ставки. Установить курсор в ячейку А1. Далее, вызвать мастер функций.
2. Из общего списка выбрать функцию ЧИСТНЗ.
3. Заполнить диалоговое окно, то есть внести необходимые аргументы функции (в поля ввода можно вводить как ссылки на ячейки, содержащие значения аргументов, так и сами значения), рис.5.
4. Завершить ввод аргументов и запуск расчета значений функции нажатием – кнопки ОК.
5. При отказе работы с функцией нажать кнопку Отмена.
Для решения следует использовать функцию ЧИСТНЗ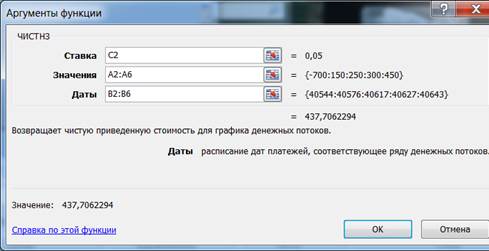 
Рис.5. Диалоговое окно ввода аргументов функции ЧИСТНЗ.
Заметим, что значение начальной выплаты должно быть введено со знаком минус.
Вид листа MS Excel представлен на рисунке 6.
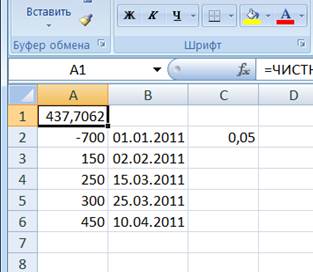
Рис.6. Вид рабочего листа.
Ответ: 437,70.
ЛАБОРАТОРНАЯ РАБОТА № 6
Получение требуемого результата путем изменения входного значения средством "Подбор параметра"
Если результат, который необходимо получить при вычислении формулы, известен, но неясно, какое входное значение формулы требуется для получения этого результата, можно использовать средство подбора параметров.
Задача:
Скрыть все
Предположим, что необходимо занять некоторую сумму денег. Известно, сколько денег требуется, на какой срок необходимо их занять и сколько можно платить каждый месяц. Определить приемлемую процентную ставку.
Средство подбора параметров поддерживает только одно входное значение переменной. Если необходимо определить несколько входных значений, например размер кредита и сумму ежемесячного платежа, следует использовать вместо этого надстройку "Поиск решения".
Технология работы:
Поскольку для достижения цели необходимо рассчитать ссудный процент, потребуется функция ПЛТ. Этафункция рассчитывает сумму ежемесячного платежа. В данной задаче эту сумму и требуется определить.
Для решения данной задачи необходимо выполнить следующие действия:
1. Откройте новый пустой лист. Сначала добавьте в первый столбец несколько названий, что упростит прочтение данных на листе.
2. В ячейку A1 введите текст Сумма ссуды.
3. В ячейку A2 введите текст Срок в месяцах.
4. В ячейку A3 введите текст Процентная ставка.
5. В ячейку A4 введите текст Платеж.
Затем добавляем известные значения.
1. В ячейку B1 введите значение 100000. Это требуемая сумма ссуды.
2. В ячейку B2 введите значение 180. Это число месяцев, за которое требуется выплатить ссуду.
Несмотря на то, что сумма платежей известна, она не вводится как значение, поскольку представляет собой результат вычисления формулы. Вместо этого на лист добавляется формула и значение платежа указывается на одном из последующих этапов при использовании средства подбора параметров.
3. Вводим формулу, для которой требуется подобрать параметры. Воспользуемся функцией ПЛТ:
В ячейку B4 введите функцию ПЛТ(B3/12;B2;B1). Эта формула вычисляет сумму платежа. В данном примере каждый месяц требуется выплачивать 900р. Это значение здесь не вводится, поскольку необходимо определить процентную ставку с помощью средства подбора параметров, а использование этого средства начинается с формулы.
Формула ссылается на ячейки B1 и B2, в которых находятся значения, указанные на предыдущих этапах. Формула также ссылается на ячейку B3, в которую средство подбора параметров поместит процентную ставку. Формула делит значение из ячейки B3 на 12, поскольку был указан ежемесячный платеж, а функция ПЛТ предусматривает использование годовой процентной ставки.
Поскольку в ячейке B3 отсутствует значение, MS Excel полагает процентную ставку равной 0% и с использованием значений из примера возвращает значение платежа 555,56 р. В данный момент это значение можно проигнорировать.
4. Наконец, отформатируем целевую ячейку B3 так, чтобы результат в ней отображался в процентном формате. На вкладке Главная в группе Число нажмите кнопку Процентный формат. Чтобы задать количество дробных разрядов, нажмите кнопку Увеличитьразрядность или Уменьшитьразрядность.
Использование средства подбора параметров для определения процентной ставки
1. На вкладке Данные в группе Средства обработки данных выберите команду Анализ условия, а затем выберите в списке пункт Подбор параметра.
2. В поле Установить в ячейке введите ссылку на ячейку, содержащую формулу, параметры которой требуется подобрать B4.
3. Введите искомый результат формулы в поле Значение. (-900). Обратите внимание на то, что число отрицательное, поскольку оно представляет собой платеж.
4. В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать $B$3.
Формула в ячейке, указанной в поле Установить в ячейке, должна ссылаться на эту ячейку. На рисунке изображен пример ввода значений.
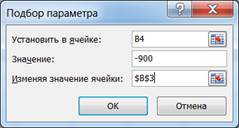
Рис.7. Подбор параметра
5. Нажмите кнопку ОК.
Средство подбора параметров проанализирует данные и выдаст результат, как показано на приведенном ниже рисунке 8.
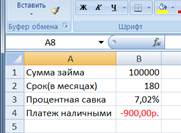
Рис.8. Вид рабочего листа.
Ответ: 7,02%.
ЛАБОРАТОРНАЯ РАБОТА № 7
Решение систем линейных алгебраических уравнений (СЛАУ)
Пусть задана СЛАУ следующего вида:
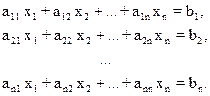
Эту систему можно представить в матричном виде: AX = b, где
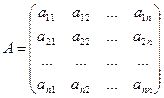- матрица коэффициентов системы уравнений,
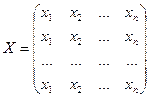– вектор неизвестных,
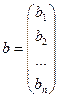– вектор правых частей.
При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо будет решать методом обратной матрицы и методом Крамера.
Основные формулы, используемые в этих методах.
Метод обратной матрицы
Систему линейных алгебраических уравнений AX = b умножим слева на матрицу, обратную к А. Система уравнений примет вид:
A-1AX=A-1b, EX=A-1b, (E – единичная матрица)
Таким образом, вектор неизвестных вычисляется по формуле X=A-1b.
Метод Крамера
В этом случае неизвестные x1,x2,…, xn вычисляются по формуле:
.
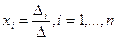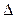– определитель матрицы А, 
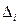– определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
Особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
Пример 1. Решить систему методом обратной матрицы:
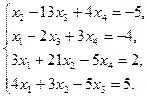
В этом случае матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:
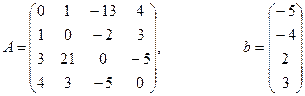
Введём матрицу A и вектор b в рабочий лист MS Excel (рис.9).
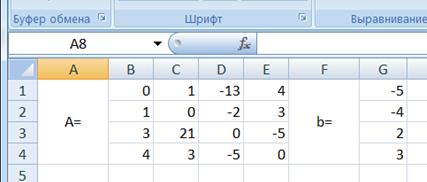
Рис.9. Ввод значений A и b
В нашем случае матрица А находится в ячейках B1:Е4, а вектор b в диапазоне G1:G4. Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы (это нужно сделать обязательно!!!); пусть в нашем случае это будут ячейки B6:E9. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР, предназначенную для вычисления обратной матрицы. В диалоговом окне, необходимо заполнить поле ввода Массив (рис. 10). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица – в нашем случае B1:E4. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
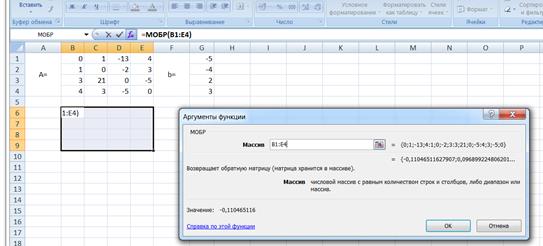
Рис.10. Поиск обратной матрицы.
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид изображенный на рис. 11.
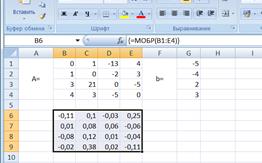
Рис.11. Обратная матрица.
Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ≠ВА
В диалоговое окно (рис.12) содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b).
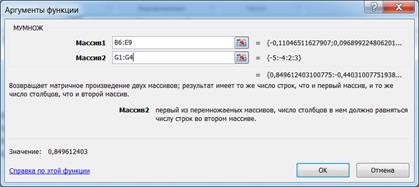
Рис.11. МУМНОЖ
Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. Результаты вычислений (вектор х), находится в ячейках H6:H9.
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор x и получить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(В1:Е4;Н6:Н9), так как было описанной выше.
В результате проведенных вычислений рабочий лист примет вид изображенный на рисунке 12.
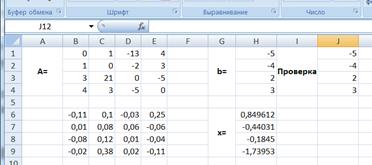
Рис.12. Результат вычислений.
Пример 2. Решить систему из Примера 1 методом Крамера.
Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рис. 13).
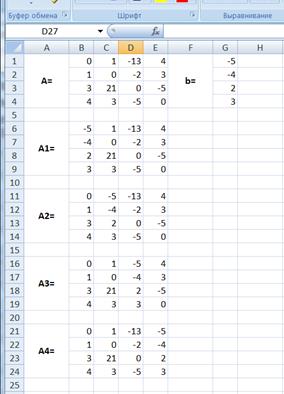
Рис.13. Подготовка рабочего листа
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B1:E4.
Для вычисления вспомогательных определителей введем формулы:
I11=МОПРЕД(B6:E9),
I12=МОПРЕД(B11:E14),
I13=МОПРЕД(B16:E19),
I14=МОПРЕД(B21:E24).
В результате в ячейке I10 хранится главный определитель, а в ячейках I11:I14 – вспомогательные.
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку K11 введём формулу: =I11/$I$10. Затем скопируем её содержимое в ячейки K12,K13 и K14. Система решена (рис.14).
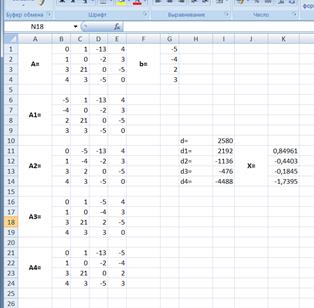
Рис.14. Результат вычислений
Пример 3. Вычислить матрицу С по формуле: C=A2+2AB, где
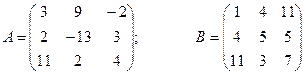
Введем исходные данные на рабочий лист и подготовим лист для вычислений (рис. 15).
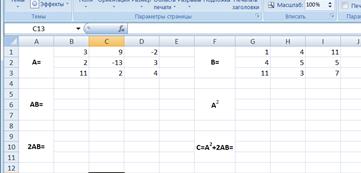
Рис.15. Рабочий лист
Для умножения матрицы А на матрицу В, выделим диапазон B5:D7 и воспользуемся функцией МУМНОЖ(B1:D3;G1:I3).
Результат вычисления A2=A*A поместим в ячейки G5:I7, воспользовавшись формулой МУМНОЖ(B1:D3;B1:D3).
Умножение (деление) матрицы на число можно выполнить при помощи элементарных операций. В нашем случае необходимо умножить матрицу из диапазона B5:D7 на число 2. Выделим ячейки B9:D11 и введем формулу =МУМНОЖ(B1:D3;G1:I3)*2.
Сложение (вычитание) матриц выполняется аналогично. Например, выделим диапазон G9:I11 и введем формулу: =B9:D11+G5:I7.
Для получения результата в обоих случаях необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.
Кроме того, в строке формул рабочего листа =МУМНОЖ(B1:D3;B1:D3)+2*МУМНОЖ(B1:D3;G1:I3), изображенного на рисунке 16, показано как можно вычислить матрицу С одним выражением.
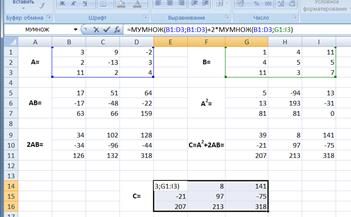
Рис.16. Результат