Модели оценки ожидаемого дохода на финансовых рынках

Изучая данный вопрос, нужно ознакомиться и понять значение построения линии рынка капиталов, линии рынка ценной бумаги и линии характеристики ЦБ. Вся три линии используются для расчета ожидаемого дохода по ценной бумаге (или портфелю ценной бумаги) Ri или R_р с учетом риска. Инвестор использует самые разнообразные приемы для изучения своего поведения на рынке ценных бумаг. Нужно осознать, что все эти расчеты определяют теоретическую цену, а фактическая складывается на финансовом рынке под воздействием спроса и предложения на капитал. Чем выше профессионализм финансового аналитика, тем точнее будет расчет ожидаемого дохода и тем более приближенной окажется теоретическая ставка дохідності к текущей.

Прежде чем перейти к формулам, вспомним немного теорию вероятности. Нормальное распределение случайных величин характеризуется двумя параметрами – матожиданием и дисперсией (нарисовать). Матожидание – это средняя величина, в нашем случае ожидаемый доход. Дисперсия же – показывает, на сколько реальный доход может отклониться от ожидаемого. Мы ведь имеем дело не с бесконечным количеством наблюдений, а всего с одним. В формулах вместо дисперсии часто используют показатель среднеквадратичного отклонения 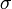, поскольку (см ниже про единицы измерения).

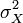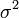Дисперсия случайной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается D[X]. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный 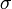, называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Из неравенства Чебышёва следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75% случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89% — не более чем на три.

2а. Линия рынка капиталов графически показывает равновесие между ожидаемым доходом и риском хорошо диверсифицированного портфеля ценных бумаг.

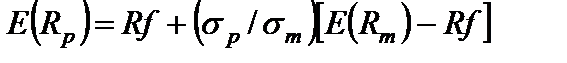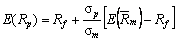Рис 2. Лінія ринку капіталів

Нахил CML показує точку вибору між доходом та ризиком:

Нахил = зміна по вертикалі доходів: зміна по горизонталі (ризик) = [E (R_m) – Rf] / s_m;

E (Rp) = 10 + (0,34/0,24) * [17 – 10] = 19,9 %; при безризиковій ставці 10 %, s_m = 0,24, s_р = 0,34, очікуваному ринковому доході 17 % можна очікувати прибуток портфеля 19,9 %.

Еще примеры:

Припустимо, що безризикова процентна ставка становить 7 %,
s_m ринкова — 0,22, s_p цінних паперів i — 0,20, цінних паперів j — 0,26, g — 0,22. Очікувана процентна ставка ринкового портфеля — 16 %. Потрібно визначити очікувану дохідність за кожним цінним папером.

1) ;

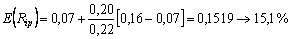2) ;

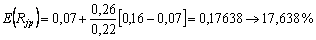3) .

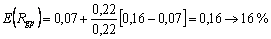Отже, очікувана дохідність портфеля цінних паперів i становить 15,1 %, що нижче ринкової. Дохід портфеля j зі ступенем ризику, вищим від ринкового, може принести інвестору дохід, вищий ринкового, в розмірі 17,6 %. Портфель g з ризиком, рівним ринковому, принесе дохід також рівний ринковому.

В дальнейших расчетах большую роль играет коэффициент b

Бета-коэффициент (бета-фактор) — показатель, рассчитываемый для ценной бумаги или портфеля ценных бумаг. Является мерой рыночного риска, отражая изменчивость доходности ценной бумаги (портфеля) по отношению к доходности портфеля (рынка) в среднем (среднерыночного портфеля).

Расчёт коэффициента

Формула расчёта коэффициента Бета для актива в составе портфеля ценных бумаг:

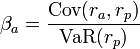, где

r_a — доходность актива

r_p — доходность портфеля ценных бумаг

Формула расчёта коэффициента Бета для актива (или портфеля) относительно рынка:

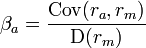, где

r_a — доходность актива (или портфеля)

r_m — доходность рынка

D — дисперсия

Cov – ковариация, т.е. мера линейной зависимости двух случайных величин.

Еще один вариант расчета (β) :

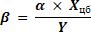
где α — корреляция между доходом от индивидуального вида ценных бумаг и средним уровнем доходности фондовых инструментов в целом;

Хцб ––среднеквадратическое отклонение уровня доходности по индивидуальному виду ценных бумаг;
Y — среднеквадратическое отклонение уровня доходности фондовых инструментов на рынке в целом в рассматриваемом периоде.

Для рыночного портфеля β = 1, для «оборонного» β < 1 для рискованного β > 1

2б. Лінія ринку цінних паперів показывает графически уравнение ожидаемого дохода по ценной бумаге как функцию безрисковой процентной ставки, беты ценной бумаги и ожидаемой прибыли рынка;

.

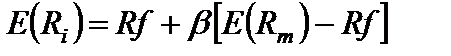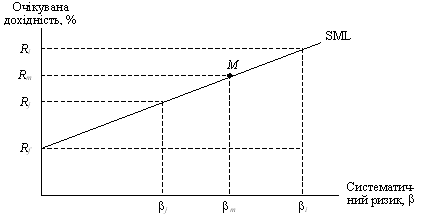
Рис. 3. Лінія ринку цінних паперів

Рыночный риск растет по мере роста дохода. Премия за риск - разница между ожидаемым доходом рынка и доходом без риска. Якщо інвестор володіє цінним папером (або портфелем цінних паперів) з β = 1, то він фактично володіє ринковим портфелем.

Например:

,

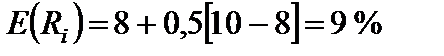тобто при b = 0,5, ставці доходу ринку 10%, безрисковой ставке 8% можна очікувати дохід по цінному паперу в розмірі 9%.

Обе линии, рассмотренных нами, имеют ту же цель: определить ожидаемый доход финансового актива с учетом риска. Однако между ими есть отличия:

Во-первых, линия рынка капиталов основана на использовании показателя общего риска (стандартного отклонения - s), тогда как линия рынка ценной бумаги - на использовании системного риска (b).

Во-вторых, линия рынка капиталов выражает равновесие между риском и доходом полностью диверсифицированного портфеля, тогда как линия рынка ценных бумаг выражает равновесие любого портфеля ценных бумаг, а также отдельной ценной бумаги.

В-третьих, на линии рынка капиталов расположены все полностью диверсифицированные портфели, тогда как отдельные ценные бумаги будут находится ниже линии (ибо для отдельной ценной бумаги s выше, чем для портфеля, т.е. при равном доходе s будет больше, либо, что то же самое, при равных s доход меньше). На линии рынка ценной бумаги расположены все портфели и ценные бумаги.

2в. Линия характеристики ценной бумаги- линия, которая показывает соотношение между доходом по отдельной ценной бумаге Ri (вертикаль) и большим портфелем (рыночным индексом) Rm (горизонталь), то есть средней рыночной ценой по данному классу ценных бумаг.

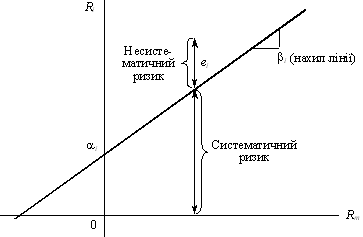
Рис 2. Линия характеристик ценной бумаги

Бета (b) показывает наклон линии характеристики. Уравнение линии характеристики:

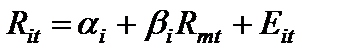(1)

де R_it — дохід по цінному паперу і у період t;

R_mt — дохід ринкового портфеля у період t;

a_i — параметр точки пересечения линии характеристики и вертикальной линии R_i у період t (коэффициент смещения);

b_i — коефіцієнт нахилу лінії характеристики;

E_{it —} случайная погрешность (при решении расчетных задач игнорируется).

Бета вираховується за формулою (есть выше):

a_i — за наступною формулою:

. (????????????)

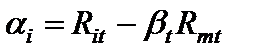Из уравнения (1) видно, что доходность ценной бумаги состоит из трех компонентов: один из них - это рыночный (систематический) компонент, представленный произведением доходности рыночного индекса на b-коэфф, второй – это собственный (несистематический) компонент, представленный a–коэффициентом, и третий компонент – случайная величина с нулевым математическим ожиданием и стандартным отклонением. Рассмотрим для примера некую ценную бумагу «А», для которой α = 2% и β = 1,2

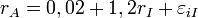
В таком случае, если доходность рыночного индекса составит 10%, то ожидаемая доходность ценной бумаги «А» будет приблизительно 14% (0,02+1,2*0,1). Если же доходность индекса составит -5%, то доходность ценной бумаг «А» будет приблизительно -4% (0,02+1,2*(-0,05)). Графически, рыночную модель можно представить следующим образом:

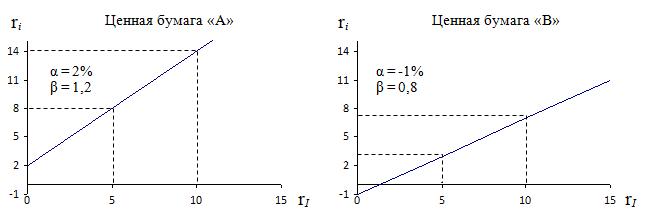
Степень наклона лини в рыночной модели измеряет чувствительность доходности ценной бумаги к доходности рыночного индекса. В обоих случаях линии имеют положительный наклон, показывающие, что с увеличением доходности рыночного индекса увеличивается и доходность ценных бумаг. Однако ценная бумага «А» имеет больший наклон, чем ценная бумага «В», что говорит о большей чувствительности доходности ценной бумаги «А» к доходности рыночного индекса. На первый взгляд, ценная бумага с большим наклоном может показаться привлекательным вложением, однако в случае падения рыночного индекса, такая ценная бумаг покажет большую величину убытка, чем убыток рыночного индекса.

В уравнении линия характеристики показывает степень изменения цены на акцию i в процентах относительно изменения рыночной цены m за определенный период t. Показатель a может быть как позитивным, так и негативным. Позитивное значение a показывает рост доходности ценной бумаги относительно среднерыночного дохода. Негативное значение a показывает снижение доходности ценной бумаги относительно рыночного дохода. В этом случае инвесторы на рынке в целом ничего не заработают.

В условиях равновесия цены a стремится к 0. На графике a является точкой пересечения линии характеристики и линии абсциссы, на которой показанные доходы, которые приносит ценная бумага i (Ri) или портфель (Rm).