Расчет стоимости продукта при изменении стоимости компонента

Пусть стоимость одного из компонентов (сырья или услуги), стоимость которого входит в стоимость продукта, возрастет на р%. Например, возрастет стоимость бензина, которая косвенно через стоимость услуги по перевозке входит в стоимость продукта.

Предположим, что стоимость компонента (бензина) составляет q% от стоимости продукта. Новая стоимость продукта может быть найдена по формуле А(1+0.0001pq).

Задача 9. На сколько увеличится цена продукта, если стоимость бензина увеличится в 2 раза, а его доля в стоимости продукта составляет 20%.

5. Сложные проценты.

Если при каждом начислении в качестве базы используется не начальная сумма, как при расчете по простым процентам, а накопленная к моменту начисления, то полученная формула называется формулой сложных процентов.

Если отсчет времени начисления начинается с момента внесения вклада и время хранения вклад равно k периодам начисления, то

S_k=S₀(1+p/m)^k , (11)

Если момент внесения вклада совпадает с началом периода начисления, то сумму, начисленную за t единиц времени хранения, вычисляем по формуле

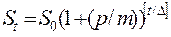, (12)

где [ ] означает взятие целой части числа,

a Δ — длительность периода начисления.

Используемые в формуле длительности необходимо задавать в одинаковых единицах времени, учитывая, что обычно в финансовых операциях полагается, что один года равен 360 дням, один месяц равен 30 дням.

Например, если вклад пролежал на депозите 2 года 16 дней, проценты начисляются ежемесячно из расчета 6% годовых, то t= 736, D=30, m=12. Следовательно, каждый рубль вклада превратится в (1+(0.06/12)[736/30])= 1+(0.06/12)24= 1.12 руб.

Если время хранения, следующее за последним начислением процентов, также учитывается при начислении, то формула (12) упрощается:

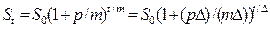, (13)

Если t исчисляется в днях, то

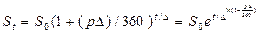, (14)

Если исчисление ведется в годах, то

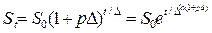, (15)

Предположим, что начисления происходят настолько часто, что Δ — очень мало. Тогда: ln(1+p Δ )=p Δ +о(Δ), получим формулу непрерывных процентов:

S_t = S₀ е ^pt , (16)

Задача 10. Используя формулы (14), (15) и (16), получить таблицу значений отношения S_t /S₀ при процентных ставках р = 0,01; 0,02; ...; 0,1; 0,2; ...; 0,5 (по столбцу) и при различных периодах начисления: ежемесячных, еженедельных, ежедневных и непрерывных (по строке), t = 1 год.

6. Применение сложных процентов в экономике.

Если налоги на продаваемую продукцию взимаются в виде процента от ее текущей стоимости, то процесс роста стоимости продаваемой продукции выражается сложными процентами. Обозначим стоимость произведенной продукции S0, процент налога — p. Тогда стоимость продукта после n перепродаж составит

S_n= (1+p)ⁿ S₀ , (17)

Задача 11. Пусть p = 10, 12, 15, 18, 20%. Во сколько раз возрастет стоимость продукции после 2, 5, 7 перепродаж. Результат оформить в виде таблицы.