Аннуитет (финансовая рента)

Важным видом денежного потока является поток с равными временными периодами 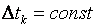и положительными элементами потока (поступлениями) 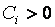. Такой поток называется финансовой рентой или аннуитетом (<anny> - год). Здесь 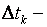период ренты, 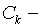член ренты.

Остальные определения таковы:

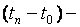 срок ренты; если срок ренты конечен, то рента считается срочной; если срок ренты неограничен, то рента называется бессрочной;

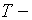 базовый период (обычно 1 год);

 если все поступления 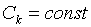, рента называется постоянный аннуитет, в противном случае она называется переменный аннуитет;

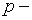 число денежных поступлений в течение базового периода 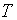; аннуитет в этом случае называется 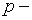срочным аннуитетом;

 если первое поступление 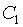поступает через 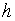периодов после момента 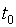, то аннуитет называют отсроченным или отложенным; в противном случае его называют немедленным;

 срочный постоянный аннуитет постнумерандо – это рентные платежи за аренду, если плата вносится регулярно в конце очередного периода; срочный аннуитет пренумерандо – это схема периодических денежных вкладов на счёт в начале каждого месяца с целью накопления; бессрочный переменный аннуитет – это схема выплаты пенсий и т. п.

Оценка аннуитета

6.3.1. Прямая задача: наращенный денежный поток

Схема постоянного аннуитета с годовым платежом 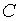и сроком 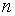лет показана на рис. 6.

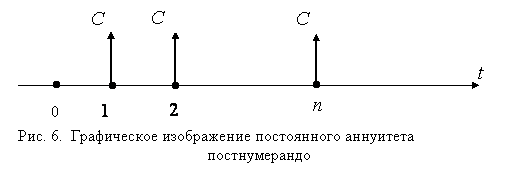
Наращенная сумма аннуитета постнумерандо получается в результате определения суммы геометрической прогрессии

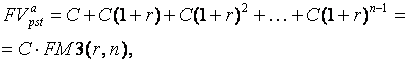(71)

где множитель наращения

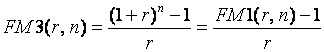. (72)

Усложним схему, положив, что в течение каждого года производится 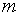раз начисление процентов:

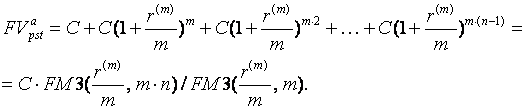(73)

Замечание. Если 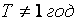, то вместо номинальной процентной ставки 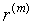берём ставку за базовый период.

Наращенная сумма аннуитета пренумерандо получается в результате определения суммы геометрической прогрессии, в которой платежи сдвинуты на начало соответствующих периодов:

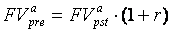. (74)

Другим обобщение схемы суммы аннуитета постнумерандо будет схема, в которой внутри годового периода имеются поступления в количестве 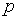раз:

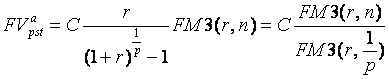. (75)

Самая общая ситуация, когда производятся внутригодовые начисления и имеются внутригодовые поступления:

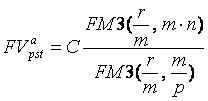. (76)

Если ввести размер годового платежа 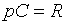, то формула (76) преобразуется к виду

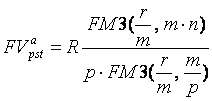, (77)

который отражает схему распределения годового платежа 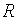по внутригодовым периодам, например, месяцам, кварталам, полугодиям.

6.3.2. Обратная задача: дисконтированный денежный поток

Обратная задача для аннуитета постнумерандо состоит в дисконтировании к начальному моменту времени всех сумм платежей:

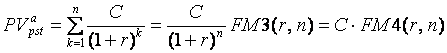, (78)

где коэффициент дисконтирования

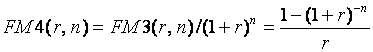. (79)

Обобщение этой схемы дисконтирования будет схема, учитывающая внутригодовые начисления и поступления:

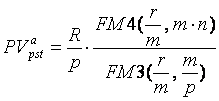. (80)

Для отсроченного аннуитета на 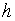периодов (необязательно целых) получим

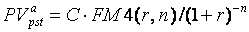. (81)

Оценка для аннуитета пренумерандо

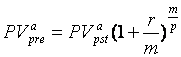. (82)