Методические указания по изучению темы

При изучении темы обратите внимание на обозначение параметров и условия применения формул, рекомендуемых для оформления контрольной работы.

Рекомендуемые обозначения

Ø i- годовая ставка процента ,

Ø Р - первоначальная денежная сумма ,

Ø S– будущая наращенная сумма,

Ø n - период, срок (в годах),

Ø 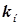- множитель наращения

Ø 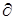- срок (в днях),

Ø K – временная база (число дней в году),

Ø d – учетная ставка.

Рекомендуемые формулы

для расчета наращенной суммы 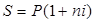, (1.1)

где 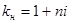; (1.2)

при плавающей ставке 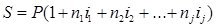, (1.3)

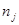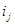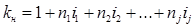где в период действует ставка и ; (1.4)

если срок задан в днях, то 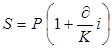; (1.5)

для математического дисконтирования 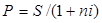, (1.6)

для банковского учета 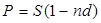. (1.7)

Типовые примеры и методы их решения рассматриваются в [3].

Литература: [1], [2], [3].

Вопросы для самоконтроля

1. Что показывает множитель наращения в формуле наращения простыми процентами?

2. В каких случаях применяют наращение по простой процентной ставке?

3. Чем отличаются точные проценты от обыкновенных?

4. Каким образом можно сравнить доходности с разными сроками?

5. Что означает консолидация платежей?

6. Что такое принцип финансовой эквивалентности?

7. Какие контракты считаются эквивалентными?

Тема 2. Сложные проценты

Начисление сложных годовых процентов. Соотношение роста по простым и сложным процентным ставкам. Начисление сложных процентов m раз в году. Множитель наращения. Номинальная и эффективная ставки. Время удвоения. Дисконтирование по сложной процентной ставке. Операции со сложной учетной ставкой. Дисконтный множитель. Непрерывное наращение и дисконтирование. Изменение условий контракта, замена платежей.

Методические указания по изучению темы

При изучении темы обратите внимание на обозначение параметров и условия применения формул, рекомендуемых для оформления контрольной работы.

Рекомендуемые обозначения

Ø i- годовая ставка процента ,

Ø Р - первоначальная денежная сумма ,

Ø S – будущая наращенная сумма,

Ø n - период, срок (в годах),

Ø 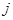- номинальная ставка при m - разовом начислении процентов

Ø 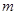- число начислений процентов в год,

Ø 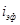– эффективная ставка,

Ø 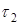– время удвоения.

Рекомендуемые формулы

для расчета наращенной суммы 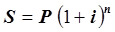; (2.1)

при m - разовом начислении процентов 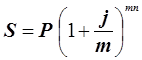; (2.2)

для точного метода 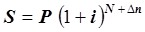, (2.3)

для смешанного метода 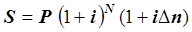(2.4)

где N – целое число периодов начисления, 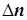- дробная часть периода;

для расчета эффективной ставки 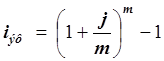; (2.5)

для расчета времени удвоения 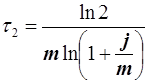, (2.6)

для математического дисконтирования 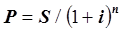(2.7)

для банковского учета 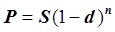. (2.8 )

Типовые примеры и методы их решения рассматриваются в [3].

Литература: [1], [3].

Вопросы для самоконтроля

1. Что называется капитализацией процентов?

2. Какие два основных способа начисления сложных процентов вы знаете? Какой из них выгоднее для кредитора?

3. Какая годовая процентная ставка называется номинальной?

4. Какая процентная ставка называется эффективной? От каких параметров она зависит?