Виды дисперсий и правило сложения дисперсий

Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в своих расчетах, мы можем определить влияние отдельных факторов, характеризующих колеблемость индивидуальных значений признака.

Это можно сделать при помощи группировок, подразделив изучаемую совокупность на группы, однородные по признаку-фактору.

При этом можно определить три показателя колеблемости признака в совокупности:

1. Общую дисперсию ( )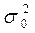

2. Межгрупповую дисперсию (δ²)

3. Среднюю из внутригрупповых дисперсий ( )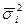

Правило сложения дисперсий позволяет находить общую дисперсию по её компонентам, когда индивидуальные значения признака неизвестны, а в распоряжении имеются только групповые показатели.

Пример.

В крае средний урожай зерновых в совхозе составил 20ц/га при среднем квадратическом отклонении 2ц/га. S под зерновыми 300 тыс. га, в колхозах 15 ц/га, σ=2,5ц/га, S₂=100тыс.га.

Найти общую среднюю урожайность зерновых по краю и среднее квадратическое отклонение.

Решение.

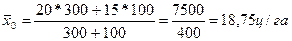
Среднее квадратическое отклонение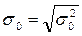

Средняя из внутригрупповых дисперсий:

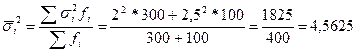
Межгрупповая дисперсия:

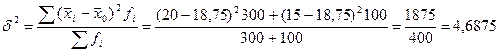
Согласно правила сложения дисперсии

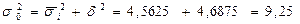
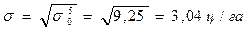
Таким образом средняя урожайность 18,75 ц/га по краю, среднее квадратическое отклонение 3,04 ц/га.

При этом общая дисперсия = 9,25,

Причем 4,6875 определена различиями в типах хозяйств, а 4,5625 падает на долю остальных.

Т.е. правило сложения дисперсий позволяет определить в общей дисперсии доли ее составных частей.

Показатель, получаемый как отношение межгрупповой дисперсии δ² к 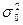называется коэффициентом детерминации.

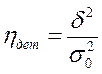
А корень квадратный из 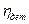- называют корреляционным отношением и используют в статистике для измерения зависимости между группировочным и результативным признаками.

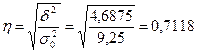
Пример.

Производительность труда двух бригад.

Бригада 1	∑	Бригада 2
№	Изготовлено деталей за час, шт. xi		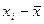( 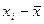)2	Изготовлено деталей за час, шт. xi		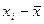( 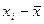)2
		-2			-3
		-1			-2
					-1
∑ 90	126 28

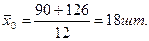
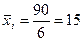
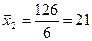
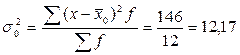
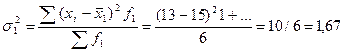
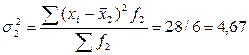
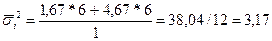
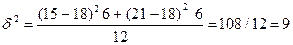
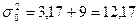
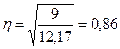
Группировочный признак существенно влияет на результативный 0,86.

Общая дисперсия

Характеризует вариацию признака, который зависит от всех условий в данной совокупности.

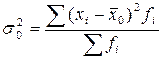, где 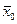- общая средняя для всей изучаемой совокупности.

Межгрупповая дисперсия

Отражает вариацию изучаемого признака, который возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних 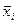около общей средней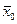

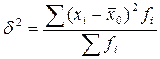, где 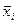- средняя по отдельным группам; 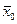- средняя общая; f_i – численность отдельных групп.