Методы детерминированного факторного анализа

Метода ДФА применяются для исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.:

1. цепной подстановки

2.абсолютных разниц

3.относительных разниц

4. индексный

5.пропорционального деления

6.долевого участия

7.интегральный

8.логарифмированный

Первые три способа ДФА основываются на методике элиминирования. Элиминировать – устранять, исключать влияние всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга. Сначала изменяется один, а все остальные без изменения, затем другой и тд. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.

В ДФА выделяются следующие типы наиболее часто встречающихся факторных моделей:

1)мультипликативные – Y=a*b*c

2) аддитивные – Y=a+b+c

3)кратные – Y=a/b

4)смешанные – Y=(a+b)/c и тд

Относительные разницы – Применяется для измерения влияния факторов на изменение результативного показателя ТОЛЬКО в мультипликативных моделях и в комбинированных типах Y=(a-b)*с

Алгоритм решения:

Y1=a1*b1*c1*d1 и Y0=a0*b0*c0*d0

Рассчитываем относительные отклонения (разницы):

Δa%= 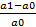*100%

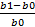Δb%= *100%

Δc%= 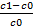*100%

Δd%= 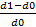*100%

Определим влияние факторов a,b,c,d на результат Y

Влияние фактора a: ΔY(a)=Y0* 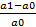*100%

Влияние фактора b: ΔY(b)=[(Y0+ΔY(a)]* 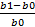*100%

Влияние фактора c: ΔY(с)=[(Y0+ΔY(a)+ ΔY(b)]* 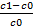*100%

Влияние фактора d: ΔY(d)=[(Y0+ΔY(a)+ ΔY(b)+ ΔY(c)]* 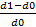*100%

Проверка: ΔY=Y1 – Y0 = [ΔY(a)+ΔY(b)+ΔY(с)+ΔY(d)]

Индексный способ:

Это метод факторного анализа, когда число факторов равно двум, один из которых количественный, а другой качественный. В основе приема лежит теория индексов из статистики. Применяется для мультипликативных и кратных моделей.

Алгоритм применения способа:

Y0=a0*b0 Y1=a1*b1

Где Y0 и Y1 – значения обобщающего показателя, соответственно базовое и фактическое.

a-количественный фактор b – качественный фактор

Индекс показателя:

Jy = (Y1/Y0) = ;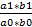

ΔY(a)=(Ja-1)*Y0; ΔY(b)=(Jb-1)*Ja*Y0

Где Ja= 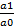; Jb= ;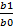

Проверка: ΔY=Y1 – Y0= ΔY(a) + ΔY(b)

Способ пропорционального деления

Он применяется для аддитивных моделей и смешанных типа: Y= a/(b+c+d)

Рассмотрим применения этого способа на примере уравнения аддитивного типа:

Y1=a1+b1+c1 и Y0=a0+b0+c0

Определим влияние факторов на результат:

На фактор a: ΔY(a)= 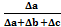*Δy

На фактор b: ΔY(b)= 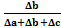*Δy

На фактор c: ΔY(c)= 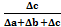*Δy

Проверка: ΔY=Y1-Y0=ΔY(a) +ΔY(b)+ΔY(c)

Способ долевого участия

Применяется для мультипликативных, кратных моделей и смешанных моделей типа Y=a/(b+c)

Алгоритм:

1. при двух факторах (a,b) влияющих на изменение обобщающего показателя Y

Y1=a1*b1 И Y0=a0+b0?

ΔY=Y1-Y0

Влияние изменения фактора а

ΔY(a)= Δa*b0 + 0,5 * Δa*Δb

Влияние изменения фактора b

ΔY(b)= Δb*a0 + 0,5 * Δa*Δb

Проверка влияния факторов на изменение обобщающего показателя балансовым приемом:

ΔY=Y1-Y0=ΔY(a) + ΔY(b)

2. при трех факторах (a,b,c), влияющих на изменение обобщающего показателя Y

Y1=a1+b1+c1 и Y0=a0+b0+c0

ΔY(a)=0,5* Δ a*(b0*c1+b1*c0) + 0,333* Δa *Δb* Δc

ΔY(b)=0,5* Δ b*(a0*c1+a1*c0) + 0,333* Δa *Δb* Δc

ΔY(c)=0,5* Δ c*(a0*b1+a1*b0) + 0,333* Δa *Δb* Δc

Проверка влияния факторов на изменение обобщающего показателя балансовым приемом

ΔY=Y1-Y0=ΔY(a)+ΔY(b)+ΔY(c)

Метод слишком трудоемкий и не находит широкого применения

Способ логарифмирования:

Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае резуль­тат расчета, как и при интегрировании, не зависит от местораспо­ложения факторов в модели и по сравнению с интегральным мето­дом обеспечивается более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факто­ров распределяется поровну между ними, то с помощью логариф­мирования результат совместного действия факторов распределя­ется пропорционально доли изолированного влияния каждого факто­ра на уровень результативного показателя. В этом его преимущество, а недостаток - в ограниченности сферы его применения.

В отличие от интегрального метода при логарифмировании ис­пользуются не абсолютные приросты результативных показателей, а индексы их роста (снижения).

Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов:

f=xyz (79)

Прологарифмировав обе части равенства, получим:

lgf=lgx+lgy+lgz (80)

Учитывая, что между индексами изменения показателей сохра­няется та же зависимость, что и между самими показателями, произ­ведем замену абсолютных их значений на индексы:

lg(f1:fo)=lg(x1:xo)+lg(y1:yo)+lg(z1:zo) (81)

или

lgIf=lgIx+lgIy+lgIz (82)

Разделив обе части равенства на lgIf и умножив на ∆f получим:

∆f=∆f(lgIx/lgIf)+∆f(lgIy/lgIf)+∆f(lgIz/lgIf)= ∆fx+∆fy+∆fz (83)

Отсюда влияние факторов определяется следующим образом:

∆fx=∆f(lgIx/lgIf) (84)

∆fy=∆f(lgIy/lgIf) (85)

∆fz=∆f(lgIz/lgIf) (86)

Из формул вытекает, что общий прирост результативного показа­теля распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя. И не имеет значения, какой логарифм используется - натуральный или десятичный [1].

Рассмотрев основные приёмы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы