Операции наращения по простым и сложным процентным ставкам
Одним из важнейших свойств денежных потоков является их распределенность во времени. При анализе относительно краткосрочных периодов (до 1 года) в условиях стабильной экономики данное свойство оказывает относительно незначительное влияние, которым часто пренебрегают. Определяя годовой объем реализации по предприятию, просто складывают суммы выручки за каждый из месяцев отчетного года. Аналогично поступают со всеми остальными денежными потоками, что позволяет оперировать их итоговыми значениями. Однако в случае более длительных периодов или в условиях сильной инфляции возникает серьезная проблема обеспечения сопоставимости данных. Одна и та же номинальная сумма денег, полученная предприятием с интервалом в 1 и более год, в таких условиях будет иметь для него неодинаковую ценность. Но проблема не сводится только к учету инфляции. Одним из основополагающих принципов финансового менеджмента является признание временной ценности денег, то есть зависимости их реальной стоимости от величины промежутка времени, остающегося до их получения или расходования. В экономической теории данное свойство называется положительным временным предпочтением.
Наряду с инфляционным обесцениванием денег существует еще как минимум три важнейшие причины данного экономического феномена. Во-первых, “сегодняшние” деньги всегда будут ценнее “завтрашних” из-за риска неполучения последних, и этот риск будет тем выше, чем больше промежуток времени, отделяющий получателя денег от этого “завтра”. Во-вторых, располагая денежными средствами “сегодня”, экономический субъект может вложить их в какое-нибудь доходное предприятие и заработать прибыль, в то время как получатель будущих денег лишен этой возможности. Расставаясь с деньгами “сегодня” на определенный период времени (допустим, давая их взаймы на 1 месяц), владелец не только подвергает себя риску их невозврата, но и несет реальные экономические потери в форме неполученных доходов от инвестирования. Кроме того снижается его платежеспособность, так как любые обязательства, получаемые им взамен денег, имеют более низкую ликвидность, чем “живые” деньги. То есть у кредитора возрастает риск потери ликвидности, и это третья причина положительного временного предпочтения. Естественно, большинство владельцев денег не согласны бесплатно принимать на себя столь существенные дополнительные риски. Поэтому, предоставляя кредит, они устанавливают такие условия его возврата, которые по их мнению полностью возместят им все моральные и материальные неудобства, возникающие у человека, расстающегося (пусть даже и временно) с денежными знаками.
Количественной мерой величины этого возмещения является процентная ставка.
С ее помощью может быть определена как будущая стоимость “сегодняшних” денег (например, если их собираются ссудить), так и настоящая (современная, текущая или приведенная) стоимость “завтрашних” денег – например, тех, которыми обещают расплатиться через год после поставки товаров или оказания услуг. В первом случае говорят об операции наращения, поэтому будущую стоимость денег часто называют наращенной. Во втором случае выполняется дисконтирование или приведение будущей стоимости к ее современной величине (текущему моменту) – отсюда термин дисконтированная, приведенная или текущая стоимость. Операции наращения денег по процентной ставке более просты и понятны, так как с ними приходится сталкиваться довольно часто беря или давая деньги взаймы.
Выделяют два вида процентных ставок:
1. Простая процентная ставка – это ставка при которой величина процента начисляется на первоначально вложенную сумм у средств; это означает, что сумма процентов за предыдущие периоды не принимается в расчет последующего наращения.
Основные формулы при определении начисленных процентов и наращенной суммы при использовании схемы простых процентов
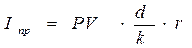(1)
где
PV – первоначальная сумма
I – сумма начисленных процентов
r – годовая процентная ставка
k – количество дней в году
d – срок начисления процентов в годах
При расчете количества дней используются несколько методик:
1. Точный процент с точным количеством дней ( год 365 (366), месяц – фактически по календарю);
2. Обыкновенный процент с приближенным числом дней (год 360 дней, месяц – 30 дней);
3. Точный процент с приближенным количеством дней (год 360 дней, месяц – фактически по календарю).
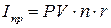(2)
n – срок начисления процентов в днях
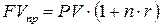(3)
FV – наращенная сумма (первоначальная сумма + начисленные проценты)
Пример 1:
Вклад в размере 160 000 рублей поместили в банк на 2 года. Определить сумму начисленных процентов при простой схеме их начисления, если банк предлагает 9 % годовых.
Решение: 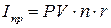= 160 000 * 2 * 0, 09 = 28 800 рублей
Пример 2:
Деньги депонированы в банк на срочный депозит на два года. Первоначальная сумма 100 000 рублей. Проценты начисляются по схеме простых процентов из расчета 12 % годовых в первый год, 13 % в последующие три месяца и 14 % годовых в оставшееся время.
Определить наращенную сумму.
Решение:
FV = 100 000 (1 + 1* 0,12 + 0,25*0,13 + 0,75 * 0,14) = 125 750 рублей.
2. Сложная процентная ставка – это ставка, при которой процент начисляется на постоянно нарастающую базу с учетом процентов, начисленных в предыдущие периоды (« проценты на процент»).
Основные формулы при определении начисленных процентов и наращенной суммы при использовании схемы сложных процентов:
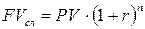(4)
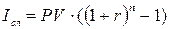(5)
Бывают ситуации, когда сложные проценты начисляются несколько раз в год (по полугодиям, кварталам и т.д.), тогда ставка на периоде начисления определяется j : m, а наращенная сумма по формуле:
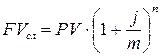(6)
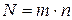
Где
j – номинальная ставка;
m - количество начислений в году.
Пример 3:
Деньги вложены в банк в сумме 5 млн. рублей на два года с полугодовым начислением процентов под 20 % годовых. В этом случае начисление процентов происходит четыре раза (два раза в год) по ставке 10 %.
Определить:
1. Сумму начисленных процентов
2. Изобразить схему возрастания капитала.
Решение:
1. 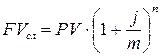= 5 млн. руб. * (1 + 0,2 : 2) 4 = 7,3205 млн. рублей
Ставка на периоде начисления, в % = 20 % : 2 = 10 %
2. Схема возрастания капитала будет иметь следующий вид:
| Период начисления в месяцах | Сумма, с которой идет начисление. млн. рублей | Ставка в долях единицы | Сумма к концу периода, млн. рублей |
| 1,1 | 5,5 | ||
| 5,5 | 1,1 | 6,05 | |
| 6,05 | 1,1 | 6,655 | |
| 6,655 | 1,1 | 7,3205 |
Таким образом, можно сделать несколько простых практических выводов:
1. Чем чаще идет начисление процентов по сложной схеме, тем больше итоговая накопленная сумма.
2. При начислении процентов 12 % годовых не эквивалентно 1 % в месяц при использовании схемы сложны процентов.
Начисление сложных процентов за дробное число лет
Достаточно обыденным являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут быть начислены по одному из двух методов:
по схеме сложных процентов
FV = PV * (1 + r ) na + nb (7)
по смешанной схеме
FV = PV * (1 + r ) na * (1 + r * nb) (8)
где
FV - наращенная сумма (сумма вклада с процентами)
PV – первоначальная сумма вклада
nb – дробная часть года
na – целая часть года
r – годовая процентная ставка
Продемонстрируем представленные методы на практическом примере.
Пример 4:
Банк предоставил ссуду в размере 10 млн. руб. на 30 месяцев под 30 % годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока?
По формуле (7)
FV = PV * (1 + r ) na + nb = 10 * (1 + 0,3 ) 2,5 = 19,27 млн. руб.
По формуле (8)
FV = PV * (1 + r ) na * (1 + r * nb) = 10 * (1 + 0,3 ) 2 * (1 + 0,3 * 0,5) = 19,44 млн. руб.
Таким образом, в условиях задачи смешанная схема начисления процентов более выгодная для банка.