Тема 6. Учет временной стоимости денег в финансовых расчетах
Концепция временной стоимости денег основывается на том, что стоимость денег с течением времени изменяется с учетом нормы прибыли на денежном рынке, в качестве которой обычно выступает норма ссудного процента (или процента). В данном случае под процентом понимается сумма доходов от использования денег на денежном рынке. Финансовые вычисления, базирующиеся на понятии временной стоимости денег, часто применяются для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудо-заемных операциях, в оценке бизнеса и других финансовых расчетах.
Рассмотрим основные понятия, связанные с учетом временной стоимости денег в финансовых расчетах.
Будущая стоимость денег представляет собой сумму инвестированных в настоящий момент средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента. Определение будущей стоимости денег связано с процессом наращенияэтой стоимости, который представляет собой поэтапное увеличение суммы вклада путем присоединения к первоначальному его размеру суммы процента (процентных платежей). Эта сумма рассчитывается по так называемой процентной ставке. В финансовых расчетах процентная ставка применяется не только как инструмент наращения стоимости денежных средств, но и в более широком смысле – как измерить степени доходности финансовых операций.
Настоящая стоимость денег представляет собой сумму будущих денежных поступлений, приведенных с учетом определенной ставки процента (так называемой «дисконтной ставки») к настоящему периоду. Определение настоящей стоимости денег связано с процессом дисконтирования этой стоимости, которая представляет собой операцию, обратную наращению при обусловленном конечном размере денежных средств. В этом случае сумма процента (дисконта) вычитается из конечной суммы (будущей стоимости) денежных средств. Такая ситуация возникает в тех случаях, когда необходимо определить сколько средств необходимо инвестировать сегодня для того, чтобы через определенный период времени получить заранее обусловленную их сумму.
При проведении финансово-экономических расчетов, связанных с ссудо-заемными операциями, процессы наращения и дисконтирования стоимости могут осуществляться как по простым, так и по сложным процентам.
Метод начисления простых процентов используется при расчете дохода кредитора при предоставлении денежных средств в долг заемщику на краткосрочный период – до одного года.
Простой процент – сумма, которая начисляется по первоначальной (настоящей) стоимости вклада в конце одного периода платежа, обусловленного условиями инвестирования средств.
Общая форма для расчета простых процентов имеет вид (формула 1):
I = K · p · n / 100= K · n · i, (1)
где I – процентный платеж;
K– первоначальный капитал;
p – годовая процентная ставка;
n – количество расчетных периодов (в годах);
i = р / 100.
Таким образом, доход кредитора через n лет составит (формула 2):
K* = K + I = К ( 1 + i · n), (2)
где К* – конечная стоимость капитала;
1 + i × n – коэффициент наращивания простых процентов.
Для определения процентного платежа, уплачиваемого за один месяц, используем формулу 3:
I = K · p / 1200. (3)
Процентный платеж, уплачиваемый за mмесяцев (формула 4):
I = K · p · m / 1200. (4)
Процентный платеж за один день (принимаем, что в году 365 дней) (формула 5):
I = K · p / 36500. (5)
Процентный платеж за dдней рассчитывается по формуле 6:
I = K · p · d / 36500. (6)
При расчете суммы простого процента в процессе дисконтирования стоимости денежных средств (суммы дисконта) используется формула 7:
Д = К* · (1 – 1 / (1 + n · i )) (7)
где 1 / ( 1 + n · i) – дисконтный коэффициент простых процентов;
Д – сумма дисконта по простым процентам за период;
К* – будущая стоимость денег.
Метод начисления сложных процентов используется при долгосрочном кредитовании.
Сложный процент – сумма дохода, который образуется в результате инвестирования при условии, что сумма начисленного простого процента не выплачивается после каждого расчетного периода, а присоединяется к сумме основного вклада и в последующем платежном периоде сама приносит доход.
Увеличение капитала по методу сложных процентов представляет собой последовательное реинвестирование средств.
Капитализация – процесс начисления процентного платежа. Может быть годовой, когда процентный платеж начисляется и добавляется к капиталу один раз в год; полугодовой – каждые 6 месяцев; квартальной – каждый квартал; месячной – каждый месяц.
Существует два метода начисления сложных процентов: декурсивный и антисипативный. При декурсивном способе начисления процентный платеж начисляется и добавляется к капиталу в конце каждого расчетного периода. Если процентный платеж начисляется в начале каждого расчетного периода – это антисипативное начисление процентов (используется в периоды высокой инфляции).
Вычисление конечной стоимости капитала при декурсивном способе расчета сложных процентов осуществляется по формуле 8:
Кn = К · (1 + р / 100 )n=К · (1 + i), (8)
где Кn –конечная стоимость капитала;
К– первоначальная стоимость капитала;
n – число периодов начисления;
р – годовая процентная ставка;
(1 + р / 100)n – коэффициент наращивания, который показывает конечную стоимость одной денежной единицы, вложенной под сложные проценты декурсивно. Для определения значения данного коэффициента можно использовать специальную финансовую таблицу, где данные коэффициенты рассчитаны для различных ставок процента и различных периодов времени.
Если доход начисляется несколько раз в году (производится полугодовая, квартальная или месячная капитализация), то используется следующая 9:
Кmn = К · ( 1 + р / 100·m)mn, (9)
где m – число расчетных периодов в году.
Вычисление конечной стоимости капитала при антисипативном способе расчета сложных процентов осуществляется по формуле 10:
Кn = К · (100 / (100 – q))n, (10)
где Кn –конечная стоимость капитала;
К – первоначальная стоимость капитала;
n – число периодов начисления;
(100 / (100 – q))n–антисипативный коэффициент наращивания.
Если доход начисляется несколько раз в году (производится полугодовая, квартальная или месячная капитализация), то используется формула 11:
Кmn = К · ( 100 · m / (100 · m – q))n, (11)
где m – число расчетных периодов в году.
В процессе операции дисконтирования денежных средств по методу сложных процентов рассчитывается настоящая стоимость денежных средств, которая выражается через конечную стоимость (формула 12):
К = Кn · (1 + р / 100)-n, (12)
где Кn – конечная стоимость капитала;
К – первоначальная стоимость капитала;
n – число периодов начисления;
(1 + р / 100)-n – коэффициент дисконтирования, показывающий первоначальную стоимость одной денежной единицы, вложенной под сложные проценты на ряд лет.
Операция дисконтирования широко используется в практике инвестиционного менеджмента для приведения денежного потока к одному моменту времени (началу процесса инвестирования), которое производится для сопоставления затрат по инвестиционному проекту и доходов по нему.
Одним из основных элементов финансового анализа является оценка денежного потока, генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта или функционирования того или иного вида активов. Денежный поток, поступаемый в начале одного временного потока называется потоком пренумерандо (или авансовым денежным потоком), денежный поток, поступаемый в конце временного периода – потоком постнумерандо.
Оценка денежного потока производится в рамках решения двух задач:
1. Прямая задача, при которой происходит оценка денежного потока с позиций будущего (реализуется схема наращения). Здесь в основе суммарной оценки наращенного денежного потока лежит формула 8.
2. Обратная задача, при который денежный поток оценивается с позиций настоящего (реализуется схема дисконтирования). Здесь определяется приведенный денежный поток согласно формуле 12.
Для потоков денежных пренумерандо и постнумерандо расчеты производятся по различным формулам.
Так, для потока постнумерандо прямая задача предполагает оценку по формуле 13:
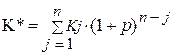, (13)
а обратная задача, предполагающая оценку денежного потока с позиций текущего момента, решается по формуле 14:
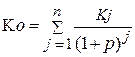. (14)
Оценка потока пренумерандо для решения прямой задачи рассчитывается по формуле 15:
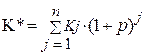, (15)
приведенная стоимость потока пренумерандо рассчитывается по формуле 16:
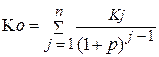. (16)
Одним из ключевых понятий в финансовых и коммерческих расчетах является понятие аннуитета, который представляет собой частный случай денежного потока.
В научной литературе выделяют два основных подхода к определению аннуитета.
Согласно первому подходу аннуитет – однонаправленный денежный поток, элементы которого имеют место через равные промежутки времени. Второй подход имеет в виду, что элементы денежного потока одинаковы по величине.
Аннуитет называется срочным, если число равных временных интервалов ограничено. Аннуитет еще называют рентой. Любое денежное поступление называют членом ренты, а величина постоянного временного интервала между двумя последовательными денежными поступлениями называют периодом аннуитета (периодом ренты).
Различают два типа аннуитетов: постнумерандо и пренумерандо.
Для оценки будущей стоимости срочного аннуитета постнумерандо (прямая задача), предполагающей регулярное поступление равных денежных потоков (А) используется формула 17:
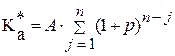, (17)
для решения обратной задачи оценки срочного аннуитета постнумерандо используется формула 18:
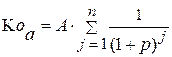. (18)
Будущая стоимость аннуитета пренумерандо будет вычисляться по формуле 19:
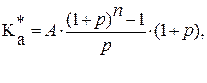(19)
аналогично приведенная стоимость аннуитета пренумерандо может быть найдена по формуле 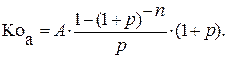20:
(20)
Аннуитет называется бессрочным (вечная рента), если денежные поступления продолжаются достаточно длительное время.
В этом случае прямая задача не имеет смысла, а обратная для бессрочного аннуитета постнумерандо определяется согласно формуле 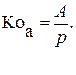21:
(21)
Эта формула показывает, что поток с неограниченным числом платежей имеет конечную приведенную стоимость.
Приведенная стоимость бессрочного аннуитета пренумерандо определяется путем прибавления к сумме приведенной стоимости бессрочного аннуитета постнумерандо суммы первого платежа.