Метод чистой современной стоимости

В последнее время в качестве основного измерителя эффективно­сти инвестиционных проектов чаще всего используется метод расчета чистой современной стоимости (NPV). Суть этого метода состоит в определении разницы между инвестиционными затратами и будущими доходами, выраженной в денежной величине, скорректированной во времени.

При разовой инвестиции чистую современную стоимость рассчи­тывают по формуле

(128)

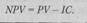Величину PV можно определить по формуле:

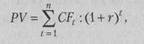(129)

где CF_t — чистый поток платежей в периоде t В таком случае получим:

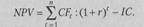(130)

Если NPV > 0, в течение своей жизни проект возместит перво­начальные затраты (инвестиции) 1С и обеспечит получение дохода; NPV < 0 показывает, что заданная сумма дохода не обеспечивается и проект убыточен. При NPV = 0 проект лишь окупает произведенные затраты, не принося дохода.

При прогнозировании доходов по годам необходимо учитывать все виды поступлений и выплат по проекту как производственного, так и непроизводственного характера: амортизационные отчисления, выс­вобождение оборотных средств, поступления от иквидации либо про­дажи оборудования по окончании проекта, которые должны включать­ся в доходы соответствующих периодов.

В тех случаях, когда денежный поток поступает равномерно в те­чение периода реализации проекта, величину PV определяют так:

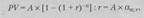(131)

где А — величина единовременного платежа;

а_пт — коэффициент приведения годовой ренты.

Тогда:

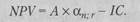(132)

Коэффициент приведения а„._г показывает величину ренты (анну­итета) с позиции текущего момента при регулярных равных денеж­ных поступлениях в течение п лет с заданной процентной ставкой г. Значения этого коэффициента табулированы (см. приложение 1).

Пример 4.

Предприятие планирует вложить средства в приобретение новой техно­логической линии, стоимость которой вместе с доставкой и установкой соста­вит 60 млн руб. Предполагается, что после пуска линии ежегодные поступле­ния после вычета налогов составят 20 млн руб. Работа линии рассчитана на 5 лет, ее ликвидационная стоимость равна затратам на демонтаж. Норма дис-

конта принята равной 12%. Экономическая эффективность проекта, опреде­ленная с помощью показателя чистой современной прибыли NPV, составит:

NPV = 20 х 3,605 - 60 = 12,1 млн руб.

Рассмотрим пример, когда инвестиции имеют разовый характер, а годовые поступления неравномерны, т.е. случай переменной ренты.

Пример 5.

Рассматривается предложение о вложении средств в инвестиционный проект сроком 4 года, в котором в первый год предполагается получить доход 20 млн руб., во второй — 25 млн руб., в третий — 30 млн руб. Поступления доходов происходят в конце каждого года, процентная ставка прогнозируется в размере 15%. Является ли это предложением выгодным, если проект требу­ет капитальных вложений в размере 50 млн руб.? Используя формулу (130), получим:

NPV = 20 : (1 + 0,15) + 25 : (1 + 0,15)² + 30 : (1 + 0Д5)³ - 50 = 6 млн руб.

В этом случае проект может бить принят.

Если проект предполагает не разовую инвестицию, а последова­тельное инвестирование ресурсов в течение нескольких лет, формула расчета NPV примет следующий вид:

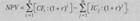(133)

где т — число лет инвестирования.

ведут, используя формулу приведенных величин рент. Если инвести­ции и поступления равномерные и дискретные, то величина NPV на­ходится как разность современных величин двух рент по формуле

(134)

где Vi — коэффициент дисконтирования;

щ — продолжительность периода инвестиций;

^п2 — продолжительность получения дохода от инвестиций.

Пример6.

Предприятие предполагает реализовать проект за 2 года. В начале пер­вого года единовременные затраты составят 20 млн руб., в начале второго — 15 млн руб. Доходы в первые 3 года планируют в размере 10 млн руб. в год, в течение следующих 2 лет — по 8 млн руб. в год. Ставка приведения планиру­ется в размере 15%. Необходимо определить сумму чистой современной стои­мости (NPV). Используя формулу (133) и коэффициенты приведения ренты, получим:

NPV= (10 х 2,283 + 8 х 1,626) - (20 + 15 : 1,15) = 2,8 млн руб.

Чистая современная стоимость потока платежей зависит от вре­менных параметров инвестиционного проекта: начала отдачи от инве­стиций и продолжительности периода отдачи. Отсрочка начала отдачи уменьшает величину современной стоимости потока доходов пропор­ционально дисконтному множителю V". В этих случаях расчет NPV ведут, используя формулу приведенных величин рент. Если инвести­ции и поступления равномерные и дискретные, то величина NPV на­ходится как разность современных величин двух рент по формуле

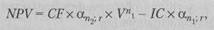
(134)

Пример 7.

Предприятие рассматривает проект, по которому инвестиции предпола­гается производить ежегодно по 10 млн руб. на протяжении 3 лет. Отдачу планируют получать ежегодно в течение 5 лет в размере 9 млн руб. Ставка приведения равна 10% годовых. Доходы будут поступать: в первом случае — сразу после завершения капитальных вложений; во втором — через 2 года после завершения инвестиций.

Определим величину чистой современной стоимости по двум вариантам. В первом случае:

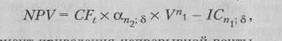(135)

NPV = 9 х 3,791 х I,!"³ - 10 х 2,487 = -3,7 млн руб.

Во втором случае:

NPV= 9 х 3,791 х 1,Г⁵ - 10 х 2,487 = -3,7 млн руб.

В тех случаях, когда вложения и отдачу можно рассматривать как непре­рывные процессы, в условиях примера 7 чистую современную стоимость мож­но определить по формуле

где а_п . _g — коэффициент приведения непрерывной ренты.

Сила роста S определяется как In 1,1 = 0,09531.

Тогда чистая современная стоимость для первого случая составит:

NPV=> 9 х (1 - 1,1"⁵) : 0,09531 х 1,1"³ - 10 х (1 - 1,Г³) : 0,09531 = = 0,8 млн руб.

Для второго случая:

NPV= 9 х (1 - ⁽1Д-⁵) : 0,09531 х 1Д"⁵ - 10 х (1 - 1Д-³) : 0,09531 = = -3,9 млн руб.

Более конкретно методика оценки эффективности производствен­ных инвестиций может быть рассмотрена на примере инвестирования средств в производство изделия А.

Чистая современная стоимость проекта определяется по форму­лам (128) и (130).

Начальные инвестиционные затраты — это чистые денежные от­токи, связанные с принятием проекта, направленные на приобретение и установку необходимых основных фондов и на реализации продукции.

Чистые денежные потоки определяются как сумма прибыли (пос­ле уплаты налогов), амортизации и других неденежных затрат (отсро­ченных платежей без добавлений к оборотному капиталу в течение изучаемого периода времени). Расчет чистых денежных потоков пред­ставлен в табл. 53.

Таблица 53