Текущая (приведенная) стоимость

d – ставка дисконтирования

Дисконтирование по простым процентам

В зависимости от вида процентной ставки при анализе краткосрочных финансовых операций применяют два метода дисконтирования – математическое и коммерческое. В первом случае в качестве нормы приведения используют ставку r, применяемую при наращении. Во втором случае в роли нормы приведения выступает учетная ставка, для обозначения которой в дальнейшем будет использоваться символ d.

Математическое дисконтирование

Математическое дисконтирование представляет собой задачу, обратную наращению, и сводится к определению величины PV по известным значениям величин FV, r, n. С учетом принятых обозначений формула дисконтирования по ставке r будет иметь следующих вид:

.

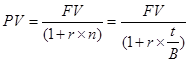Разность FV – PV называют дисконтом, или скидкой, а используемую норму приведения к – декурсивной ставкой процентов.

Пример. Какую цену заплатит инвестор за бескупонную облигацию с номиналом в 100, 00 ед. и погашением через 90 дней, если требуемая норма доходности 12%?

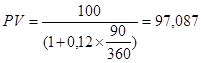ед.

Банковский, или коммерческий, учет

Этот метод дисконтирования применяется в основном при банковской учете векселей. Суть его заключается в том, что проценты начисляются на сумму, подлежащую уплате в конце срока операции. При этом применяется учетная ставка d. Формула дисконтирования по учетной ставке имеет следующий вид:

.

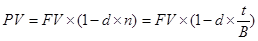Пример. Простой вексель на сумму 100 000 ед. с оплатой через 90 дней учитывается в банке немедленно после получения. Учетная тавка банка 15%. Определить сумму, полученную владельцем векселя.

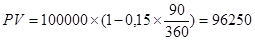
Соответственно, банк удержал в свою пользу 100 000 – 96 250 = 3 750

Дисконтирование по сложным процентам

Для вычисления настоящей стоимости вклада в процессе дисконтирования по сложным процентам (PV) используют формулу:

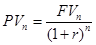
Пример. Вычислить необходимую сумму вклада, чтобы при ставке в 10% за год, через 4 года получить 6000 руб.

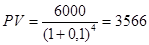
Если начисление процентов осуществляется m раз в году, соотношение будет иметь следующий вид:

.

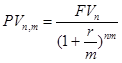Оценка срочных аннуитетов

Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют финансовой рентой, или аннуитетом.

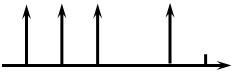
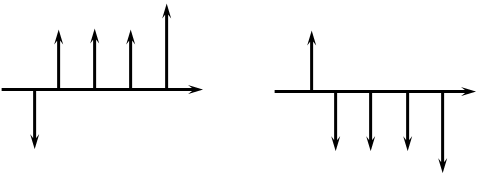Теоретически, в зависимости от условий формирования, могут быть получены весьма разнообразные виды аннуитетов: с платежами равной либо произвольной величины; с осуществлением выплат в начале, середине или конце периода и др. в финансовой практике встречаются так называемые простые, или обыкновенные, аннуитеты, которые предполагают получение или выплаты одинаковых по величине сумм на протяжении всего срока операции в конце каждого периода) года, полугодия, квартала, месяца и т.д.). Схематично подобный денежный поток может представлен следующим образом (Рисунок 21).

Рисунок 21. Аннутитеты

Выплата по купонным облигациям, банковским кредитам, долгосрочной аренде, страховым полисам, формирование различных фондов – все это далеко не полный перечень финансовых операций, денежные потоки которых представляют собой обыкновенные аннуитеты.

Согласно определению простой аннуитет обладает двумя важными свойствами:

Все его n элементов равны между собой

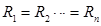
Отрезки времени между выплатой / получением сумм одинаковы

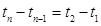
Выделяют 2 типа аннуитетов: постнумерандо и пренумерандо.

Рисунок 22. Виды аннутитетов

Примером срочного аннуитета постнумерандо могут служить регулярно поступающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истечении очередного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления достаточной суммы для крупной покупки.

На практике большее распространений получил поток постнумерандо, в частности, именно этот поток лежит в основе методик анализа инвестиционных проектов. Некоторые объяснения этому можно дать исходя из общих принципов учета, согласно которым принято подводить итоги и оценивать финансы результат того или иного действия по окончании очередного отчетного периода. Что касается поступления денежных средств в счет оплаты, то на практике оно чаще всего распределено во времени неравномерно и потому удобнее условно отнести все поступления к концу периода.

Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.

Оценка денежного потока может выполняться в рамках решения двух задач:

Прямой, т.е. проводится оценка с позиции будущего (реализуется схема наращения)

Обратной, т.е. проводится оценка с позиции настоящего (реализуется схема дисконтирования).

При расчете будущей стоимости аннуитета на условиях предварительных платежей (пренумерандо) используется следующая формула:

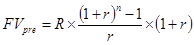, где

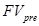– будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо);

R – член аннуитета, характеризующий размер отдельного платежа;

r – используемая процентная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример:Ежегодно в начале года в банк делается очередной взнос в размере 1000 руб. Банк платит 10% годовых. Какая сумма будет на счете по истечении пяти лет?

Подставляя эти значения в приведенную формулу, получим:

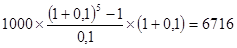
При расчете будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется следующая формула

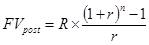, где

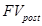– будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо);

R – член аннуитета, характеризующий размер отдельного платежа;

r – используемая процентная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Вам предлагают сдать в аренду участок на 5 лет. Выбрав один из двух варинтов:

1 000 руб. в конце каждого года;

6 000 руб. в конце пятилетнего периода.

Какой вариант более предпочтителен, если банк предлагает 10% по вкладу

Подставляя эти данные в приведенную формулу, получим:

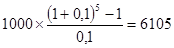усл. ден. единиц.

Таким образом, расчет показывает, первый вариант более выгоден.

При расчете настоящей стоимости аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), используется следующая формула:

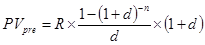, где

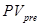– настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо);

R – член аннуитета, характеризующий размер отдельного платежа;

d – используемая процентная (дисконтная) ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать настоящую стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), при следующих данных.

период платежей по аннуитету предусмотрен в количестве 5 лет;

интервал платежей по аннуитету составляет один год (при внесении платежей в начале года);

сумма каждого отдельного платежа (члена аннуитета) составляет 1 000 руб.;

используемая для дисконтирования стоимости ставка процента (дисконтная ставка) составляет 10% в год (0,1).

Подставляя эти значения в приведенную формулу, получим:

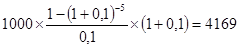руб.

При расчете настоящей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется следующая формула:

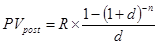, где

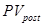– настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо);

R – член аннуитета, характеризующий размер отдельного платежа;

d – используемая процентная (дисконтная) ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать настоящую стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо) по данным, изложенным в предыдущем примере (при условии взноса платежей в конце года).

Подставляя эти данные в приведенную формулу, получим:

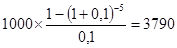руб.

Сопоставление результатов расчета по двум последним примерам показывает, что настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей, существенно превышает настоящую стоимость аннуитета, осуществляемого на условиях последующих платежей, т.е. в первом случае в процессе дисконтирования плательщику гарантирована гораздо большая сумма дохода в настоящей стоимости.

При расчете размера отдельного платежа при заданной будущей стоимости аннуитета используется следующая формула:

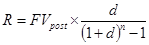, где

R – размер отдельного платежа по аннуитету (член аннуитета при предопределенной будущей его стоимости);

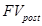– будущая стоимость аннуитета (осуществляемого на условиях последующих платежей);

d – используемая процентная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени.

При расчете размера отдельного платежа при заданной текущей стоимости аннуитета используется такая формула:

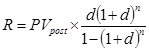, где

R – размер отдельного платежа по аннуитету (член аннуитета при известной текущей его стоимости);

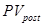– настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей);

d – используемая процентная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени.

В процессе расчета аннуитета возможно использование упрощенных формул, основу которых составляет только член аннуитета (размер отдельного платежа) и соответствующий стандартный множитель (коэффициент) его наращения или дисконтирования.

В этом случае формула для определения будущей стоимости аннуитета (осуществляемого на условиях последующих платежей), имеет вид :

,

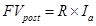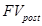– будущая стоимость аннуитета (осуществляемого на условиях последующих платежей);

R – член аннуитета, характеризующий размер отдельного платежа;

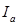– множитель наращения стоимости аннуитета, определяемый по специальным таблицам, с учетом принятой процентной ставки и количества интервалов в периоде платежей.

Соответственно, формула для определения настоящей стоимости аннуитета имеет вид :

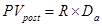, где

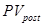– настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей);

R – член аннуитета, характеризующий размер отдельного платежа;

– дисконтный множитель аннуитета, определяемый по специальным таблицам, с учетом принятой процентной (дисконтной) ставки и количества интервалов в периоде платежей.

Первый шаг в решении любой задачи. Связанной с расчетом временной стоимости денег, - это изучение схемы денежных потоков с тем, чтобы отобразить её на временном графике. Вуди Ален говорил, что 90% успеха – это обратить на себя внимание. Что же касается задач, связанных с временной стоимостью денег, 90% успеха – это правильное определение моментов и условий совершения денежных потоков.

После того как вы отобразите денежные потоки на графике, следующий ваш шаг – выбрать верный способ решения задачи. Какой из подходов вы выберете – численный, использование финансового калькулятора или электронную таблицу? Ответ на этот вопрос зависит от конкретной ситуации.

Существуют специальные финансовые таблицы, с помощью которых при заданных размерах ставки процента и количества платежных периодов можно определить будущую и настоящую стоимость денежных средств.