Операции дисконтирования по простым и сложным процентным ставкам
Однако для финансового менеджмента значительно более важное значение имеет дисконтирование денежных потоков, приведение их будущей стоимости к современному моменту времени для обеспечения сопоставимости величины распределенных по времени платежей.
В принципе, дисконтирование – это наращение “наоборот”, однако для финансовых расчетов важны детали, поэтому необходимо более подробно рассмотреть как прямую, так и обратную задачу процентных вычислений. Прежде чем рассматривать их применительно к денежным потокам, следует усвоить наиболее элементарные операции с единичными суммами (разовыми платежами).
Дисконтирование – это процесс нахождения первоначальной суммы исходя из величины наращенной суммы; другими словами это приведение прогнозируемых денежных поступлений к текущему моменту времени с использованием определенного коэффициента дисконтирования.
Дисконтирование можно осуществлять по двум схемам:
1. схеме простых процентов
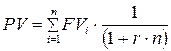(9)
2. схеме сложных процентов
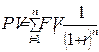(10)
Пример 5:
Прогнозируются денежные поступления в течении трех лет: первый год – 150 000 рублей, второй – 160, третий – 200 000 рублей. Определить приведенную стоимость прогнозируемых денежных поступлений, если коэффициент дисконтирования 20 % (сложные проценты).
Решение:
| Годы | Прогнозируемые денежные поступления | Множитель дисконтирования, при r = 20 % | Приведенная стоимость |
| 150 000 | 0,833 | 124 950 | |
| 160 000 | 0,694 | 111 040 | |
| 200 000 | 0,579 | 115 800 | |
| Итого: | 510 000 | - | 352 790 |
Таким образом, «сегодняшняя стоимость» прогнозируемых в течении трех лет 510 000 с учетом коэффициента дисконтирования 20 % составляет 352 790 рублей (что меньше на 157 210 рублей)
4. 3. Определение приведенной и будущей стоимости денежных потоков
Основные правила процентных вычислений, рассмотренные нами ранее, остаются неизменными и для совокупности платежей, однако возникает необходимость ввести несколько дополнительных понятий. В финансовом анализе для обозначения денежных потоков в наиболее общем смысле используется термин рента.
Каждый отдельный рентный платеж называют членом ренты. Частным случаем ренты является финансовая рента или аннуитет – такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними. Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет. В буквальном переводе “аннуитет” подразумевает, что платежи происходят с интервалом в один год, однако встречаются потоки с иной периодичностью выплат. Очевидно, что рента – это более широкое понятие, чем аннуитет, так как существует множество денежных потоков, члены которых не равны друг другу или распределены неравномерно.
Параметры ренты:
Наряду с членом ренты (обозначим его R) любой денежный поток характеризуется рядом других параметров:период ренты (t) – временной интервал между двумя смежными платежами; срок ренты(n) – общее время, в течение которого она выплачивается; процентная ставка (i) – ставка сложного процента, используемая для наращения и дисконтирования платежей, из которых состоит рента.
В зависимости от числа платежей за период различают годовые и p-срочные ренты. По величине членов денежного потока ренты могут быть постоянными (с равными членами) и переменными.
Рассмотрим пример определения будущей величины ограниченной постоянной ренты (аннуитета) постнумерандо которая выплачивается 1 раз в год (p = 1) и проценты по которой начисляются по сложной эффективной процентной ставке i 20% годовых также 1 раз в год (m = 1). Размер годового платежа R составляет 3 тыс. рублей, общий срок ренты n равен 5 годам.
Наращение денежного потока
| № периода | Итого | |||||
| 1.Член ренты, тыс. руб. | ||||||
| 2.Время до конца ренты, периодов (лет) | – | |||||
| 3.Множитель наращения | (1+0,2)4 | (1+0,2)3 | (1+0,2)2 | (1+0,2)1 | (1+0,2)0 | – |
| 4.Наращенная величина, тыс. руб. (стр.1*;стр.3) | 6,22 | 5,18 | 4,32 | 3,6 | 22,32 |
Полученное значение (22,32 тыс. руб.) заметно больше арифметической суммы отдельных членов ренты (15 тыс. руб.), однако она значительно меньше той гипотетической суммы, которая могла быть получена, если бы мы захотели нарастить по ставке 20% все 15 тыс. руб. за весь срок ренты (15*; 1,25). Наращенная сумма ренты S получена путем последовательного начисления процентов по каждому члену ренты и последующего суммирования полученых результатов. Введя обозначение k = номеру периода ренты, в наиболее общей форме данный процесс можно выразить следующей формулой:
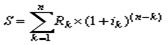(11)
В нашем примере член ренты R неизменен в течение всего срока, процентная ставка i также постоянна. Поэтому наращенную величину ренты можно найти как сумму геометрической прогрессии с первым членом 3000 и знаменателем (1 + 0,2):
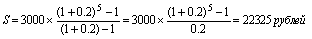
Следовательно, от общей формулы наращения ренты (11) можно перейти к ее частному случаю – формуле наращения аннуитета:
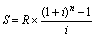(12)
Наращение денежных потоков имеет место при периодическом внесении на банковский депозит фиксированных сумм с целью накопления финансового фонда к определенному моменту времени.
Например, разместив долгосрочный облигационный заем, предприятие готовится к погашению суммы основного долга в конце срока займа путем периодического внесения на банковский счет фиксированных платежей под установленный процент. Таким образом к моменту погашения облигационного займа у предприятия накопятся достаточные средства в этом фонде. Аналогичные задачи решаются в ходе формирования пенсионного фонда или при накоплении суммы для оплаты обучения детей. Например, заботясь о своей старости, человек может наряду с обязательными отчислениями в государственный Пенсионный фонд, вносить часть своего ежемесячного заработка на банковский депозит под проценты. Наращение суммы такого вклада будет происходить по описанному выше алгоритму.
Обратный по отношению к наращению процесс – дисконтирование денежного потока имеет еще большую важность для финансового менеджмента, так как в результате определяются показатели, являющиеся в настоящее время основными критериями принятия финансовых решений. Рассмотрим этот процесс более подробно. Предположим, что рассмотренный в нашем примере денежный поток характеризует планируемые поступления от реализации инвестиционного проекта. Доходы должны поступать в конце периода. Так как эти поступления планируется получить в будущем, а инвестиции, необходимые для выполнения проекта, должны быть произведены уже сегодня, предприятию необходимо сопоставить величину будущих доходов с современной величиной затрат. Как уже было сказано выше, использование для сравнения арифметической суммы членов потока (15 тыс. руб.) бессмысленно, так как эта сумма не учитывает влияние фактора времени. Для обеспечения сопоставимости данных величина будущих поступлений должна быть приведена к настоящему моменту, иными словами данный денежный поток должен быть дисконтирован по ставке 20%. Предприятие сможет определить сегодняшнюю стоимость будущих доходов. При этом процентная ставка будет выступать в качестве измерителя альтернативной стоимости этих доходов: она показывает, сколько денег могло бы получить предприятие, если бы разместило приведенную (сегодняшнюю) стоимость будущих поступлений на банковский депозит под 20%.
Дисконтирование денежного потока предполагает дисконтирование каждого его отдельного члена с последующим суммированием полученных результатов. Для этого используется дисконтный множитель математического дисконтирования по сложной процентной ставке i. Операции наращения и дисконтирования денежных потоков взаимообратимы, то есть наращенная сумма ренты может быть получена начислением процентов по соответственной сложной ставке i на современную (приведенную) величину этой же ренты (S = PV*; (1+i)n).
Дисконтирование денежного потока
| № периода | Итого | |||||
| 1.Член ренты, тыс. руб. | ||||||
| 2. Число лет от начальной даты | ||||||
| 3.Множитель дисконтирования | 1/(1+0,2)1 | 1/(1+0,2)2 | 1/(1+0,2)3 | 1/(1+0,2)4 | 1/(1+0,2)5 | – |
| 4.Приведенная величина, тыс. руб. (стр.1*; стр.3) | 2,5 | 2,08 | 1,74 | 1,45 | 1,21 | 8,98 |
Из таблицы видно, что при альтернативных затратах 20% сегодняшняя стоимость будущих доходов составляет 8,98 тыс. руб. Именно эта величина и должна сравниваться с инвестициями для определения целесообразности принятия проекта или отказа от его реализации. Обобщая алгоритм, по которому выполнялись расчеты, получаем общую формулу дисконтирования денежных потоков:
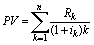(13)
Так как в нашем примере i и R постоянные величины, то снова применяя правило суммирования геометрической прогрессии, получим частную формулу дисконтирования аннуитета:
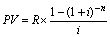(14)
Рассмотренный выше пример можно было найти по формуле (14)
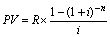= 3 *( (1 – (1+0,2)-5 ) : 0,2) = 8,98 тыс. рублей.
Пример 6:
Создается фонд денежных средств путем внесения на депозит по 100 000 в конце каждого года. Банк платит 11 % годовых. Проценты начисляются раз в год по схеме сложных процентов.