КЛЮЧИ: Правильный ответ: первый во всех вопросах

Для итогового контроля

Задача 1.

Ссуда в размере 6 млн. руб. дана на 1 год с условием возврата 9 млн. руб. Найти процентную ставку и дисконт.

Ответы:

1. процентная ставка r = 50%, дисконт d = 33.33%

2. процентная ставка r = 60%, дисконт d = 44.44%

3. процентная ставка r = 100%, дисконт d = 66.66%

4. процентная ставка r = 30%, дисконт d = 33.33%

Задача 2.

Ссуда в размере 5 млн. руб. дана на 1 год с условием возврата 6 млн. руб. Найти процентную ставку и дисконт.

Ответы:

1. процентная ставка r = 20%, дисконт d = 16.67%

2. процентная ставка r = 30%, дисконт d = 44.44%

3. процентная ставка r = 25%, дисконт d = 16.67%

4. процентная ставка r = 10%, дисконт d = 5.33%

Задача 3.

Ссуда в размере 20 млн. руб. дана на 1 год с условием возврата 21 млн. руб. Найти процентную ставку и дисконт.

Ответы:

1. процентная ставка r = 5%, дисконт d = 4.76%

2. процентная ставка r = 6%, дисконт d = 4.44%

3. процентная ставка r = 10%, дисконт d = 6.66%

4. процентная ставка r = 3%, дисконт d = 2.33%

Задача 4.

Кредит выдан на 12 млн. руб. с кредитной ставкой 12.5% годовых. Сколько следует вернуть через год?

Ответы:

1. 13.5 млн.

2. 14.5 млн.

3. 11.5 млн.

4. 12.5 млн.

Задача 5.

Кредит выдан на 16 млн. руб. с кредитной ставкой 13% годовых. Сколько следует вернуть через год?

Ответы:

5. 18.08 млн.

6. 17.98 млн.

7. 18.83 млн.

8. 21.3 млн.

Задача 6.

Кредит выдан на 12 млн. руб. с кредитной ставкой 25% годовых. Сколько следует вернуть через год?

Ответы:

9. 15 млн.

10. 17 млн.

11. 18 млн.

12. 13 млн.

Задача 7.

Кредит выдан с условием возврата через год 12 млн. руб. и дисконтом 30%. Сколько получит дебитор?

Ответы:

1. 8.4 млн.

2. 9.4 млн.

3. 8.6 млн.

4. 7.4 млн.

Задача 8.

Кредит выдан с условием возврата через год 21 млн. руб. и дисконтом 12%. Сколько получит дебитор?

Ответы:

1. 18.48 млн.

2. 19.44 млн.

3. 18.65 млн.

4. 17.47 млн.

Задача 9.

Кредит выдан с условием возврата через год 150 млн. руб. и дисконтом 9%. Сколько получит дебитор?

Ответы:

1. 136.5 млн.

2. 139.4 млн.

3. 148.6 млн.

4. 137.4 млн.

Задача 10.

Выдан кредит на сумму 12 млн. руб. с 15.01.2005 г. по 15.03. 2005 г. под 20% годовых. Найти сумма погасительного платежа при расчете по обыкновенным и точным процентам.

Ответы:

1. По обыкновенным процентам S(t) =12.6 млн. и по точным процентам S(t) =12.592 млн.

2. По обыкновенным процентам S(t) =14 млн. и по точным процентам S(t) =13.958904 млн.

3. По обыкновенным процентам S(t) =13.241 млн. и по точным процентам S(t) =13.436 млн.

4. По обыкновенным процентам S(t) =12.6 млн. и по точным процентам S(t) =12.238450 млн.

Задача 11.

Выдан кредит на сумму 12 млн. руб. с 15.01.2007 г. по 15.03. 2007 г. под 18% годовых. Найти сумма погасительного платежа при расчете по обыкновенным и точным процентам.

Ответы:

1. По обыкновенным процентам S(t) =12.54 млн. и по точным процентам S(t) =12.533 млн.

2. По обыкновенным процентам S(t) =13.34 млн. и по точным процентам S(t) =13.958904 млн.

3. По обыкновенным процентам S(t) =12.241788 млн. и по точным процентам S(t) =13.56млн.

4. По обыкновенным процентам S(t) =12.44 млн. и по точным процентам S(t) =12.845 млн.

Задача 12.

Выдан кредит на сумму 12 млн. руб. с 15.01.2007 г. по 15.07 2007 г. под 18% годовых. Найти сумма погасительного платежа при расчете по обыкновенным и точным процентам.

Ответы:

1. По обыкновенным процентам S(t) =13.09 млн. и по точным процентам S(t) =13.071 млн.

2. По обыкновенным процентам S(t) =13.19 млн. и по точным процентам S(t) =13.195894 млн.

3. По обыкновенным процентам S(t) =13.241 млн. и по точным процентам S(t) =13.346 млн.

4. По обыкновенным процентам S(t) =14.08 млн. и по точным процентам S(t) =14.238 млн.

Задача 13.

Ссуда в размере 60 тыс. руб. выдана на полгода по простой ставке процентов 12% годовых. Определить наращенную сумму.

Ответы:

1. Наращенную сумму S(t) = 63.6 тыс. руб.

2. Наращенную сумму S(t) = 64.6 тыс. руб.

3. Наращенную сумму S(t) = 63.8 тыс. руб.

4. Наращенную сумму S(t) = 63.9 тыс. руб.

Задача 14.

Ссуда в размере 320 тыс. руб. выдана на полгода по простой ставке процентов 8% годовых. Определить наращенную сумму.

Ответы:

1. Наращенную сумму S(t) = 322.8 тыс. руб.

2. Наращенную сумму S(t) = 334.6 тыс. руб.

3. Наращенную сумму S(t) = 343.8 тыс. руб.

4. Наращенную сумму S(t) = 323.9 тыс. руб.

Задача 15.

Ссуда в размере 320 тыс. руб. выдана на 9 месяцев по простой ставке процентов 8% годовых. Определить наращенную сумму.

Ответы:

1. Наращенную сумму S(t) = 339.2 тыс. руб.

2. Наращенную сумму S(t) = 344.6 тыс. руб.

3. Наращенную сумму S(t) = 323.8 тыс. руб.

4. Наращенную сумму S(t) = 333.9 тыс. руб.

Задача 16.

Кредит в размере 30 млн. руб. выдан 2 марта до 11 декабря под 30% годовых, год високосный. Определить размер наращенной суммы для различных вариантов расчета процентов: точное число дней ссуды и точная длительность года 366 дней (точные проценты); приближенные число дней ссуды и приближенная длительность года 360 дней (обыкновенные проценты).

Ответы:

1. По точным процентам S(t) =36.984 млн. руб, по обыкновенным процентам S(t) =37 млн. руб

2. По точным процентам S(t) =36.984 млн. руб., по обыкновенным процентам S(t) =37.168 млн. руб.

3. По точным процентам S(t) =37.084 млн. руб., по обыкновенным процентам S(t) =37.345 млн. руб

4. По точным процентам S(t) =36.126 млн. руб., по обыкновенным процентам S(t) =37 млн. руб

Задача 17.

Определить период начисления, за который первоначальный капитал в размере 38 млн. руб. вырастет до 40 млн. руб., если используется простая ставка процентов 12% годовых.

Ответы:

1. t = 0.438596 года = 160 дней.

2. t = 0.538596 года = 192 дня.

3. t = 0.468596 года = 171 дней.

4. t = 0.513596 года = 189 дней.

Задача 18.

Определить период начисления, за который первоначальный капитал в размере 50 млн. руб. вырастет до 52 млн. руб., если используется простая ставка процентов 12% годовых.

Ответы:

1. t = 0.333 года

2. t = 0.538 года

3. t = 0.468 года

4. t = 0.444 года

Задача 19.

Определить период начисления, за который первоначальный капитал в размере 50 млн. руб. вырастет до 52 млн. руб., если используется простая ставка процентов 10% годовых.

Ответы:

1. t = 0.4 года

2. t = 0.333 года

3. t = 0.368 года

4. t = 0.444 года

Задача 20.

Определить простую ставку процентов, при которой первоначальный капитал в размере 60 млн. руб. достигнет 63 млн. руб. через полгода.

Ответы:

1. r = 10%

2. r = 12%

3. r = 8%

4. r = 5%

Задача 21.

Определить простую ставку процентов, при которой первоначальный капитал в размере 60 млн. руб. достигнет 63 млн. руб. через квартал.

Ответы:

1. r = 20%

2. r = 22%

3. r = 28%

4. r = 25%

Задача 22.

Определить простую ставку процентов, при которой первоначальный капитал в размере 160 млн. руб. достигнет 163 млн. руб. через полгода.

Ответы:

1. r = 3.75%

2. r = 1.2%

3. r = 1.8%

4. r = 3.5%

Задача 23.

Кредит выдается под простую ставку 16% годовых на 250 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 50 млн. руб.

Ответы:

1. сумма, получаемая заемщиком S(0) =45 млн. руб., сумму процентных денег 5 млн. руб.

2. сумма, получаемая заемщиком S(0) =48 млн. руб., сумму процентных денег 2 млн. руб.

3. сумма, получаемая заемщиком S(0) =43 млн. руб., сумму процентных денег 7 млн. руб.

4. сумма, получаемая заемщиком S(0) =44 млн. руб., сумму процентных денег 6 млн. руб.

Задача 24.

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании простой ставки процентов в размере 18% годовых.

Ответы:

1. Наращенная сумма S(t) = 380 тыс. руб.

2. Наращенная сумма S(t) = 280 тыс. руб.

3. Наращенная сумма S(t) = 400 тыс. руб.

4. Наращенная сумма S(t) = 390 тыс. руб.

Задача 25.

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании сложной ставки процентов в размере 8% годовых.

Ответы:

1. Наращенная сумма S(t) = 293.866 тыс. руб.

2. Наращенная сумма S(t) = 280.347 тыс. руб.

3. Наращенная сумма S(t) = 242.7940 тыс. руб.

4. Наращенная сумма S(t) = 390.472 тыс. руб.

Задача 26.

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании сложной ставки процентов в размере 18% годовых. Рассмотреть случай, когда сложные проценты начисляются ежегодно.

Ответы:

1. Наращенная сумма S(t) = 457.551 тыс. руб.

2. Наращенная сумма S(t) = 458.551 тыс. руб.

3. Наращенная сумма S(t) = 457.651 тыс. руб.

4. Наращенная сумма S(t) = 459.795 тыс. руб.

Задача 27.

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании сложной ставки процентов в размере 18% годовых. Рассмотреть случай, когда сложные проценты начисляются по полугодиям.

Ответы:

1. Наращенная сумма S(t) = 473.473 тыс. руб.

2. Наращенная сумма S(t) = 468.551 тыс. руб.

3. Наращенная сумма S(t) = 477.651 тыс. руб.

4. Наращенная сумма S(t) = 481.795 тыс. руб.

Задача 28.

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании сложной ставки процентов в размере 8% годовых. Рассмотреть случай, когда сложные проценты начисляются по полугодиям.

Ответы:

1. Наращенная сумма S(t) = 296.049 тыс. руб.

2. Наращенная сумма S(t) = 268.551 тыс. руб.

3. Наращенная сумма S(t) = 277.651 тыс. руб.

4. Наращенная сумма S(t) = 281.795 тыс. руб.

Задача 29.

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании сложной ставки процентов в размере 18% годовых. Рассмотреть случай, когда сложные проценты начисляются поквартально.

Ответы:

1. Наращенная сумма S(t) = 482.343 тыс. руб.

2. Наращенная сумма S(t) = 498.591 тыс. руб.

3. Наращенная сумма S(t) = 477.651 тыс. руб.

4. Наращенная сумма S(t) = 499.795 тыс. руб.

Задача 30.

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании сложной ставки процентов в размере 8% годовых. Рассмотреть случай, когда сложные проценты начисляются поквартально.

Ответы:

1. Наращенная сумма S(t) = 297.189 тыс. руб.

2. Наращенная сумма S(t) = 298.591 тыс. руб.

3. Наращенная сумма S(t) = 277.651 тыс. руб.

4. Наращенная сумма S(t) = 299.795 тыс. руб.

Задача 31

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании ставки процентов в размере 18% годовых. Рассмотреть случай, когда проценты начисляются непрерывно.

Ответы:

1. Наращенная сумма S(t) = 491.921 тыс. руб.

2. Наращенная сумма S(t) = 498.591 тыс. руб.

3. Наращенная сумма S(t) = 477.651 тыс. руб.

4. Наращенная сумма S(t) = 499.795 тыс. руб.

Задача 32

Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании ставки процентов в размере 8% годовых. Рассмотреть случай, когда проценты начисляются непрерывно.

Ответы:

1. Наращенная сумма S(t) = 298.365 тыс. руб.

2. Наращенная сумма S(t) = 298.591 тыс. руб.

3. Наращенная сумма S(t) = 277.651 тыс. руб.

4. Наращенная сумма S(t) = 299.795 тыс. руб.

Задача 33.

Первоначальная сумма долга равна 150 млн. руб. Определить наращенную сумму долга через 2,5 года, используя способ начисления смешанных процентов по ставке 25% годовых.

Ответы:

1. Наращенная сумма S(t) = 263.672 млн. руб.

2. Наращенная сумма S(t) = 278.591 млн. руб.

3. Наращенная сумма S(t) = 277.651 млн. руб.

4. Наращенная сумма S(t) = 299.795 млн. руб.

Задача 34.

Первоначальная сумма долга равна 150 млн. руб. Определить наращенную сумму долга через 3.5 года, используя способ начисления смешанных процентов по ставке 14% годовых.

Ответы:

1. Наращенная сумма S(t) = 237.788 млн. руб.

2. Наращенная сумма S(t) = 248.591 млн. руб.

3. Наращенная сумма S(t) = 237.651 млн. руб.

4. Наращенная сумма S(t) = 249.795 млн. руб.

Задача 35.

Первоначальная сумма долга равна 10 млн. руб. Определить наращенную сумму долга через 2,25 года, используя способ начисления смешанных процентов по ставке 20% годовых.

Ответы:

1. Наращенная сумма долга S(t) = 15.12 млн. руб.

2. Наращенная сумма долга S(t) = 15.46 млн. руб.

3. Наращенная сумма долга S(t) = 15.62 млн. руб.

4. Наращенная сумма долга S(t) = 15.01 млн. руб.

Задача 36.

Первоначальная сумма долга равна 10 млн. руб. Определить наращенную сумму долга через 2,25 года, используя способ начисления смешанных процентов по ставке 10% годовых.

Ответы:

1. Наращенная сумма долга S(t) = 12.4025 млн. руб.

2. Наращенная сумма долга S(t) = 12.4634 млн. руб.

3. Наращенная сумма долга S(t) = 12.6225 млн. руб.

4. Наращенная сумма долга S(t) = 12.3175 млн. руб.

Задача 37.

31 марта 2005 г. была получена в долг сумма 140 тыс. руб. под 20% годовых. Долг был возвращен 11 июня 2009 г. Какая сумма была возвращена?

Ответы:

1. S(t) = 301.755 тыс. руб.

2. S(t) = 303.755 тыс. руб.

3. S(t) = 302.755 тыс. руб.

4. S(t) = 306.755 тыс. руб.

Задача 38.

31 марта 2005 г. была получена в долг сумма 140 тыс. руб. под 10% годовых. Долг был возвращен 11 июня 2009 г. Какая сумма была возвращена?

Ответы:

1. S(t) = 209.016тыс. руб.

2. S(t) = 203.755 тыс. руб.

3. S(t) = 202.755 тыс. руб.

4. S(t) = 226.755 тыс. руб.

Задача 39.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него начисляются сложные проценты по ставке 14% годовых?

Ответы:

1. t = 7.4856 года

2. t = 7.0856 года

3. t = 7.9856 года

4. t = 7.1856 года

Задача 40.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него начисляются сложные проценты по ставке 10% годовых?

Ответы:

1. t = 10.2909 года

2. t = 9.0856 года

3. t = 9.9856 года

4. t = 10.1856 года

Задача 41.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него начисляются два раза в год сложные проценты по ставке 14% годовых?

Ответы:

1. t = 7.2484 года

2. t = 7.0856 года

3. t = 7.9856 года

4. t = 7.1856 года

Задача 42.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него начисляются два раза в год сложные проценты по ставке 10% годовых?

Ответы:

1. t = 10.0515 года

2. t = 10.0856 года

3. t = 10.9856 года

4. t = 10.1856 года

Задача 43.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него ежеквартально начисляются сложные проценты по ставке 14% годовых?

Ответы:

1. t = 7.1278 года

2. t = 7.0856 года

3. t = 7.9856 года

4. t = 7.1856 года

Задача 44.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него ежеквартально начисляются сложные проценты по ставке 10% годовых?

Ответы:

1. t = 9.9304 года

2. t = 9.0856 года

3. t = 9.9856 года

4. t = 9.1856 года

Задача 45.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него непрерывно начисляются проценты по ставке 14% годовых?

Ответы:

1. t = 7.0059 года

2. t = 7.0856 года

3. t = 7.9856 года

4. t = 7.1856 года

Задача 46.

За какой срок первоначальный капитал 150 млн. руб. увеличится до 400 млн. руб., если на него непрерывно начисляются проценты по ставке 10% годовых?

Ответы:

1. t = 9.8083 года

2. t = 9.0856 года

3. t = 9.9856 года

4. t = 9.1856 года

Задача 47.

Если цены растут на 2% ежемесячно, то часто за годовой уровень инфляции принимают 24% , и банки привлекают клиентов, обещая 25%. Каков уровень инфляции? Какую прибыль имеют клиенты банка?

Ответы:

1. i = 26.82%, убытки - 1.82%
2. i = 24.00%, прибыль 1.00%
3. i = 23.53%, прибыль 1.47%
4. i = 25.14%, убытки - 0.14%

Задача 48.

Если цены растут на 1% ежемесячно, то часто за годовой уровень инфляции принимают 12% , и банки привлекают клиентов, обещая 12.5%. Каков уровень инфляции? Какую прибыль имеют клиенты банка?

Ответы:

1. i = 12.68%, убытки - 0.18%
2. i = 12.00%, прибыль 0.50%
3. i = 13.53%, прибыль 1.03%
4. i = 12.64%, убытки - 0.14%

Задача 49.

Вексель выдан на сумму 12 млн. руб. и содержит обязательство выплатить владельцу эту сумму 15.03.2009 г. Владелец предъявил банку вексель досрочно 01.02.2009 г., банк согласился выплатить сумму (учесть вексель), но с дисконтом 20% годовых. Найти полученную сумму.

Ответы:

1. S(0) = 11.7 млн. руб.

2. S(0) = 11.1 млн. руб.

3. S(0) = 11.3 млн. руб.

4. S(0) = 11.6 млн. руб.

Задача 50.

Вексель выдан на сумму 12 млн. руб. и содержит обязательство выплатить владельцу эту сумму 15.03.2007 г. Владелец предъявил банку вексель досрочно 01.02.2007 г., банк согласился выплатить сумму (учесть вексель), но с дисконтом 20% годовых. Найти полученную сумму.

Ответы:

1. S(0) = 11.7 млн. руб.

2. S(0) = 11.1 млн. руб.

3. S(0) = 11.3 млн. руб.

4. S(0) = 11.6 млн. руб.

Задача 51.

Определить современную (текущую, настоящую, приведенную) величину суммы 150 млн. руб., выплачиваемую через три года при использовании ставки сложных процентов 14% годовых.

Ответы:

1. S(0) = 101.246 млн. руб.

2. S(0) = 101.731 млн. руб.

3. S(0) = 111.749 млн. руб.

4. S(0) = 112.157 млн. руб.

Задача 52.

Определить современную (текущую, настоящую, приведенную) величину суммы 150 млн. руб., выплачиваемую через три года при использовании ставки сложных процентов 9% годовых.

Ответы:

1. S(0) = 115.8275 млн. руб.

2. S(0) = 111.731 млн. руб.

3. S(0) = 121.749 млн. руб.

4. S(0) = 112.157 млн. руб.

Задача 53.

Вексель на 12 млн. руб. с годовой учетной ставкой 12% с дисконтированием 4 раза в год выдан на 2 года. Найти исходную сумму, которая должна быть выдана в долг под вексель.

Ответы:

1. S(0) = 9.405 млн. руб.

2. S(0) = 10.147 млн. руб.

3. S(0) = 10.357 млн. руб.

4. S(0) = 9.697 млн. руб.

Задача 54.

Вексель на 12 млн. руб. с годовой учетной ставкой 12% с дисконтированием 2 раза в год выдан на 2 года. Найти исходную сумму, которая должна быть выдана в долг под вексель.

Ответы:

1. S(0) = 9.369 млн. руб.

2. S(0) = 9.147 млн. руб.

3. S(0) = 10.357 млн. руб.

4. S(0) = 9.697 млн. руб.

Задача 55.

Найти эффективную ставку сделки, в результате которой первоначальный капитал утроился за 10 лет.

Ответы:

1. r = 11.61%

2. r = 10.7%

3. r = 11.7%

4. r = 12.3%

Задача 56.

Найти эффективную ставку сделки, в результате которой первоначальный капитал утроился за 6 лет.

Ответы:

5. r = 20.1%

6. r = 19.7%

7. r = 21.7%

8. r = 18.3%

Задача 57

Найти средний годовой темп роста ВВП, при котором ВВП удвоится за 10 лет.

Ответы:

1. r = 7.2%

2. r = 7.8%

3. r = 6.9%

4. r = 7.1%

Задача 58.

Найти средний годовой темп роста ВВП, при котором ВВП удвоится за 8 лет.

Ответы:

1. r = 9.05%

2. r = 9.18%

3. r = 8.97%

4. r = 9.01%

Задача 59.

Найти средний годовой темп роста ВВП, при котором ВВП удвоится за 5 лет.

Ответы:

1. r = 14.87%

2. r = 17.18%

3. r = 16.9%

4. r = 17.13%

Задача 60.

В долг дана сумма 2 млн. руб. Через 2,5 года следует вернуть 3.5 млн. руб. Найти эффективную ставку в данной сделке.

Ответы:

1. r = 25.09%

2. r = 24.87%

3. r = 22.63%

4. r = 24.16%

Задача 61.

В долг дана сумма 2 млн. руб. Через 4.5 года следует вернуть 3.5 млн. руб. Найти эффективную ставку в данной сделке.

Ответы:

1. r = 13.24%

2. r = 14.87%

3. r = 12.63%

4. r = 14.16%

Задача 62.

Выдан кредит в 2 млн. руб. на 3 месяца под 16% годовых. Найти эффективную ставку, учитывая, что кредит краткосрочный.

Ответы:

1. r = 17.0%

2. r = 16.4%

3. r = 17.1%

4. r = 16.3%

Задача 63.

Выдан кредит в 2 млн. руб. на 3 месяца под 12% годовых. Найти эффективную ставку, учитывая, что кредит краткосрочный.

Ответы:

1. r = 12.55%

2. r = 12.15%

3. r = 12.31%

4. r = 12.33%

Задача 64.

Вексель 15 млн. руб. выдан на 3 года с годовой учетной ставкой 10% с дисконтированием 2 раза в год. Найти эффективную ставку.

Ответы:

1. r = 10.8%

2. r = 11.3%

3. r = 13.5%

4. r = 11.9%

Задача 65.

Вексель 15 млн. руб. выдан на 3 года с годовой учетной ставкой 8% с дисконтированием 2 раза в год. Найти эффективную ставку.

Ответы:

1. r = 8.5%

2. r = 8.3%

3. r = 9.5%

4. r = 8.9%

Задача 66.

Остров Манхеттен был продан в 1624 г. за $ 24. В 1976 г. его стоимость была $ 40×10⁹. Какова эффективная ставка сделки?.

Ответы:

1. r = 6.2%

2. r = 107.3%

3. r = 228.5%

4. r = 569.6%

Задача 67.

Остров Манхеттен был продан в 1624 г. за $ 24. В 1976 г. его стоимость была $ 40×10⁹. Используя эффективную ставку, оценить современную стоимость Манхеттена на 2008 год.

Ответы:

1. $275.7 млрд.
2. $295.8 млрд.
3. $287.2 млрд.
4. $245.9 млрд.

Задача 68.

Ссуда 100 тыс. руб. дана на 3,5 года под ставку 8% годовых с ежеквартальным начислением. Найти сумму конечного платежа и эффективную ставку сделки.

Ответы:

1. S(t) = 131948 руб., r = 8.24%.
2. S(t) = 141948 руб., r = 8.14%.
3. S(t) = 121048 руб., r = 8.05%.
4. S(t) = 137948 руб., r = 8.65%.

Задача 69.

Ссуда 100 тыс. руб. дана на 3,5 года под ставку 12% годовых с ежеквартальным начислением. Найти сумму конечного платежа и эффективную ставку сделки.

Ответы:

1. S(t) = 151259 руб., r = 12.55%.

2. S(t) = 141948 руб., r = 12.14%.

3. S(t) = 161048 руб., r = 12.05%.

4. S(t) = 157948 руб., r = 12.65%.

Задача 70.

Вексель на 18 млн. руб. с годовой учетной ставкой 8% и дисконтированием 4 раза в год выдан на 4 года. Найти исходную сумму, которая должна быть выдана в долг под этот вексель, и эффективную ставку сделки.

Ответы:

1. S(0) = 13.028 млн. руб., r = 8.42%.
2. S(0) = 14.128 млн. руб., r = 6.24%.
3. S(0) = 15.321 млн. руб., r = 4.42%.
4. S(0) = 13.751 млн. руб., r = 8.03%.

Задача 71.

Вексель на 18 млн. руб. с годовой учетной ставкой 12% и дисконтированием 4 раза в год выдан на 4 года. Найти исходную сумму, которая должна быть выдана в долг под этот вексель, и эффективную ставку сделки.

Ответы:

1. S(0) = 11.056 млн. руб., r = 12.96%.

2. S(0) = 11.128 млн. руб., r = 12.24%.

3. S(0) = 12.321 млн. руб., r = 14.42%.

4. S(0) = 13.751 млн. руб., r = 12.03%.

Задача 72.

Инфляция в течение года меняется по линейному закону. В начале года она равна 15% в конце года она равна 5%. В начале года у господина А имеется сумма 50 тыс. руб. Какова реальная стоимость этой суммы к концу года, если господин А держит деньги в «чулке»? Под какой процент должны быть вложены деньги, чтобы они не обесценились?

Ответы:

1. 45.24 млн. руб., r >= 10.0%

2. 46.24 млн. руб., r >= 10.2%

3. 44.24 млн. руб., r >= 11.0%

4. 43.24 млн. руб., r >= 10.7%

Задача 73

Инфляция в течение года меняется по линейному закону. В начале года она равна 5% в конце года она равна 15%. В начале года у господина А имеется сумма 50 тыс. руб. Какова реальная стоимость этой суммы к концу года, если господин А держит деньги в «чулке»? Под какой процент должны быть вложены деньги, чтобы они не обесценились?

Ответы:

1. 45.24 млн. руб., r >= 10.0%

2. 46.24 млн. руб., r >= 10.2%

3. 44.24 млн. руб., r >= 11.0%

4. 43.24 млн. руб., r >= 10.7%

Задача 74.

Инфляция в течение года меняется по закону i = -15 t²+12 (%), где 0<t<1 – время в годах. В начале года у господина А имеется сумма 100 тыс. руб. Какова реальная стоимость этой суммы к концу года, если господин А держит деньги в «чулке»? Под какой процент должны быть вложены деньги, чтобы они не обесценились?

Ответы:

1. 93.24 млн. руб., r >= 7.0%

2. 96.24 млн. руб., r >= 10.2%

3. 94.24 млн. руб., r >= 9.2%

4. 93.24 млн. руб., r >= 10.7%

Задача 75.

Инфляция в течение года меняется по закону i = -12t²+11 (%), где 0<t<1 – время в годах. В начале года у господина А имеется сумма 100 тыс. руб. Какова реальная стоимость этой суммы к концу года, если господин А держит деньги в «чулке»? Под какой процент должны быть вложены деньги, чтобы они не обесценились?

Ответы:

1. 93.24 млн. руб., r >= 7.0%

2. 96.24 млн. руб., r >= 8.2%

3. 94.24 млн. руб., r >= 6.2%

4. 93.24 млн. руб., r >= 7.7%

Задача 76.

Контракт предусматривает следующий порядок использования кредитной линии: 01.07.2007 г. – 15 млн. руб., 1.01.2008 г. – 9 млн. руб., 01.01.2010 г. – 18 млн. руб. Необходимо определить сумму задолженности на начало 2011 г., при условии, что проценты начисляются по ставке 10% годовых.

Ответы:

1. S(t) = FV =52.72 млн. руб.

2. S(t) = FV =56.72 млн. руб.

3. S(t) = FV =52.13 млн. руб.

4. S(t) = FV =53.17 млн. руб.

Задача 77.

Контракт предусматривает следующий порядок использования кредитной линии: 01.07.2007 г. – 15 млн. руб., 1.01.2008 г. – 9 млн. руб., 01.01.2010 г. – 18 млн. руб. Необходимо определить современную стоимость этого потока на начало срока при условии, что проценты начисляются по ставке 10% годовых.

Ответы:

1. S(0) = PV =37.76млн. руб.

2. S(0) = PV =36.92млн. руб.

3. S(0) = PV =37.97млн. руб.

4. S(0) = PV =35.24млн. руб.

Задача 78.

Контракт предусматривает следующий порядок использования кредитной линии: 01.07.2007 г. – 30 млн. руб., 1.01.2008 г. – 18 млн. руб., 01.01.2010 г. – 36 млн. руб. Необходимо определить сумму задолженности на начало 2011 г., при условии, что проценты начисляются по ставке 10% годовых.

Ответы:

5. S(t) = FV =105.44 млн. руб.

6. S(t) = FV =106.72 млн. руб.

7. S(t) = FV =102.13 млн. руб.

8. S(t) = FV =103.17 млн. руб.

Задача 79.

Контракт предусматривает следующий порядок использования кредитной линии: 01.07.2007 г. – 30 млн. руб., 1.01.2008 г. – 18 млн. руб., 01.01.2010 г. – 36 млн. руб. Необходимо определить современную стоимость этого потока на начало срока при условии, что проценты начисляются по ставке 10% годовых.

Ответы:

1. S(0) = PV =75.52млн. руб.

2. S(0) = PV =76.92млн. руб.

3. S(0) = PV =77.97млн. руб.

4. S(0) = PV =75.24млн. руб.

Задача 80.

Кредит 120 тыс. руб. погашается 12 равными ежемесячными взносами. Найти сумму выплат при ставке 12% годовых.

Ответы:

1. С = 10.662 тыс. руб.

2. С = 10.761 тыс. руб.

3. С = 10.137 тыс. руб.

4. С = 10.312 тыс. руб.

Задача 81.

Кредит 100 тыс. руб. погашается 10 равными ежемесячными взносами. Найти сумму выплат при ставке 12% годовых.

Ответы:

1. С = 10.558 тыс. руб.

2. С = 10.761 тыс. руб.

3. С = 10.137 тыс. руб.

4. С = 10.312 тыс. руб.

Задача 82.

Кредит 240 тыс. руб. погашается 12 равными ежемесячными взносами. Найти сумму выплат при ставке 12% годовых.

Ответы:

5. С = 21.324 тыс. руб.

6. С = 20.761 тыс. руб.

7. С = 20.137 тыс. руб.

8. С = 20.312 тыс. руб.

Задача 83.

Кредит 200 тыс. руб. погашается 10 равными ежемесячными взносами. Найти сумму выплат при ставке 12% годовых.

Ответы:

5. С = 21.116 тыс. руб.

6. С = 21.761 тыс. руб.

7. С = 21.137 тыс. руб.

8. С = 20.312 тыс. руб.

Задача 84. (Ипотека)

Для приобретения недвижимости стоимостью 130 тыс. $ берется кредит под 18% годовых. Согласно контракту погашение кредита происходит каждый месяц в течение 20 лет. Какова сумма месячного платежа?

Ответы:

1. С = $2006

2. С = $2013

3. С = $2037

4. С = $2105

Задача 85. (Ипотека)

Для приобретения недвижимости стоимостью 130 тыс. $ берется кредит под 6% годовых. Согласно контракту погашение кредита происходит каждый месяц в течение 30 лет. Какова сумма месячного платежа?

Ответы:

1. С = $779

2. С = $879

3. С = $709

4. С = $915

Задача 86. (Ипотека)

Для приобретения недвижимости стоимостью 130 тыс. $ берется кредит под 3% годовых. Согласно контракту погашение кредита происходит каждый месяц в течение 20 лет. Какова сумма месячного платежа?

Ответы:

1. С = $721

2. С = $737

3. С = $821

4. С = $797

Задача 87. (Ипотека)

Для приобретения недвижимости стоимостью 200 тыс. $ берется кредит под 18% годовых. Согласно контракту погашение кредита происходит каждый месяц в течение 20 лет. Какова сумма месячного платежа?

Ответы:

1. С = $3086

2. С = $3013

3. С = $3037

4. С = $3105

Задача 88. (Ипотека)

Для приобретения недвижимости стоимостью 200 тыс. $ берется кредит под 6% годовых. Согласно контракту погашение кредита происходит каждый месяц в течение 30 лет. Какова сумма месячного платежа?

Ответы:

1. С = $1198

2. С = $1879

3. С = $1109

4. С = $1215

Задача 89. (Ипотека)

Для приобретения недвижимости стоимостью 130 тыс. $ берется кредит под 3% годовых. Согласно контракту погашение кредита происходит каждый месяц в течение 20 лет. Какова сумма месячного платежа?

Ответы:

1. С = $1109

2. С = $1137

3. С = $1221

4. С = $1097

Задача 90.

Кредит 100 тыс. руб. выдан банком на 10 месяцев под 12% годовых. Договор предусматривает дополнительные ежемесячные выплаты на обслуживание кредита в размере 1% от суммы кредита и комиссионный сбор в момент заключения сделки в размере 2% от суммы кредита. Найти размер месячного платежа и эффективную ставку сделки.

Ответы:

1. С = 10.558 тыс. руб. r = 28.69%

2. С = 10.914 тыс. руб. r = 20.36%

3. С = 11.570 тыс. руб. r = 38.36%

4. С = 10.021 тыс. руб. r = 16.12%

Задача 91.

Кредит 100 тыс. руб. выдан банком на 10 месяцев под 12% годовых. Договор предусматривает дополнительные ежемесячные выплаты на обслуживание кредита в размере 1% от суммы кредита. Найти размер месячного платежа и эффективную ставку сделки.

Ответы:

1. С = 10.558 тыс. руб. r = 25.61%

2. С = 10.914 тыс. руб. r = 20.36%

3. С = 11.570 тыс. руб. r = 38.36%

4. С = 10.021 тыс. руб. r = 16.12%

Задача 92.

Кредит 100 тыс. руб. выдан банком на 10 месяцев под 12% годовых. Договор предусматривает комиссионный сбор в момент заключения сделки в размере 2% от суммы кредита. Найти размер месячного платежа и эффективную ставку сделки.

Ответы:

1. С = 10.558 тыс. руб. r = 15.45%

2. С = 10.914 тыс. руб. r = 20.36%

3. С = 11.570 тыс. руб. r = 18.36%

4. С = 10.021 тыс. руб. r = 16.12%

Задача 93.

Кредит 100 тыс. руб. выдан банком на 10 месяцев под 12% годовых. Найти размер месячного платежа и эффективную ставку сделки.

Ответы:

1. С = 10.558 тыс. руб. r = 12.68%

2. С = 10.914 тыс. руб. r = 13.36%

3. С = 11.570 тыс. руб. r = 18.36%

4. С = 10.021 тыс. руб. r = 16.12%

Задача 94.

Для приобретения автомобиля стоимостью $ 80 тыс. ежеквартально в течение 5 лет в банк под 8% годовых откладывается сумма С. Найти сумму ежеквартального платежа С.

Ответы:

1. С = $ 3293

2. С = $ 2975

3. С = $ 3803

4. С = $ 2426

Задача 95.

Для приобретения автомобиля стоимостью $ 120 тыс. ежеквартально в течение 5 лет в банк под 8% годовых откладывается сумма С. Найти сумму ежеквартального платежа С.

Ответы:

5. С = $ 4939.5

6. С = $ 4975.4

7. С = $ 4803.6

8. С = $ 4426.9

Задача 96.

В момент рождения ребенка начинают откладывать ежемесячно $C на его обучение в университете. Плата за весь срок обучение составляет $50 тыс. и вносится в момент поступления ребенка в университет. Ребенок поступает в университет в возрасте 17 лет. Банковская ставка составляет 6% в год. Найти величину $C.

Ответы:

1. С = $ 142

2. С = $ 162

3. С = $ 139

4. С = $ 123

Задача 97.

В момент рождения ребенка начинают откладывать ежемесячно $C на его обучение в университете. Плата за весь срок обучение составляет $100 тыс. и вносится в момент поступления ребенка в университет. Ребенок поступает в университет в возрасте 17 лет. Банковская ставка составляет 6% в год. Найти величину $C.

Ответы:

5. С = $ 284

6. С = $ 262

7. С = $ 239

8. С = $ 223

Задача 98

Контракт между фирмой и банком предусматривает, что банк предоставляет в течение 3 лет кредит фирме ежегодными платежами в размере 2млн. $ в начале каждого года под ставку 10% годовых. Фирма возвращает долг, выплачивая 2 млн., 4 млн. и 2 млн. $ последовательно в конце 3, 4-го и 5-го года.

Найти чистый приведенный доход (S(o) = NPN) для банка. Приемлема ли сделка для инвестора?

Ответы:

1. S(o) = NPN = $ 0.00545млн., да

2. S(o) = NPN = $ 0.00545млн., нет

3. S(o) = NPN = $ - 0.00545млн., да

4. S(o) = NPN = $ 0.150475млн., да

Задача 99

Контракт между фирмой и банком предусматривает, что банк предоставляет в течение 3 лет кредит фирме ежегодными платежами в размере 4 млн. $ в начале каждого года под ставку 10% годовых. Фирма возвращает долг, выплачивая 4 млн., 8 млн. и 2 млн. $ последовательно в конце 3, 4-го и 5-го года.

Найти чистый приведенный доход (S(o) = NPN) для банка. Приемлема ли сделка для инвестора?

Ответы:

1. S(o) = NPN = $ 0.0109млн., да

2. S(o) = NPN = $ 0.01545млн., нет

3. S(o) = NPN = $ - 0.01345млн., да

4. S(o) = NPN = $ 0.150475млн., да

Задача 100.

Ссуда в 20 млн. руб. выдана под 12% годовых (т.е. 1% месячных) и требует ежемесячной оплаты по 260 тыс. руб. и выплаты остатка долга к концу срока в 10 лет. Каков остаток долга D?

Ответы:

1. D = 2.307 млн. руб.

2. D = 3.234 млн. руб.

3. D = 1.953 млн. руб.

4. D = 2.928 млн. руб.

Задача 101.

Ссуда в 40 млн. руб. выдана под 12% годовых (т.е. 1% месячных) и требует ежемесячной оплаты по 260 тыс. руб. и выплаты остатка долга к концу срока в 10 лет. Каков остаток долга D?

Ответы:

1. D = 4.614 млн. руб.

2. D = 3.234 млн. руб.

3. D = 3.953 млн. руб.

4. D = 2.928 млн. руб.

Задача 102.

Сравнить эффективность трех сделок:

1. В начале первого года банк дает фирме кредит в размере 3 млн. руб. В конце второго года фирма возвращает 4 млн. руб.

2. Банк дает фирме кредит два этапа: в начале первого года – 2 млн. руб., в начале второго года – 1 млн. руб. В конце второго года фирма возвращает 4 млн. руб.

3. Банк дает фирме кредит два этапа: в начале первого года – 1 млн. руб., в начале второго года – 2 млн. руб. В конце второго года фирма возвращает 4 млн. руб.

Ответы:

1. r₁ = 15.45%, r₂ = 18.59%, r₃ = 23.59%

2. r₁ = 16.45%, r₂ = 19.49%, r₃ = 25.53%

3. r₁ = 15.05%, r₂ = 19.97%, r₃ = 21.51%

4. r₁ = 14.12%, r₂ = 17.78%, r₃ = 13.17%

Задача 103.

Сравнить эффективность трех сделок:

1. В начале первого года банк дает фирме кредит в размере 5 млн. руб. В начале второго года фирма возвращает 2 млн. руб. В конце второго года фирма возвращает 4 млн. руб.

2. Банк дает фирме кредит два этапа: в начале первого года – 3 млн. руб., в начале второго года – 2 млн. руб. В конце второго года фирма возвращает 6 млн. руб.

3. Банк дает фирме кредит два этапа: в начале первого года – 2 млн. руб., в начале второго года – 3 млн. руб. В конце второго года фирма возвращает 6 млн. руб.

Ответы:

1. r₁ = 11.63%, r₂ = 11.95%, r₃ = 13.73%

2. r₁ = 10.45%, r₂ = 12.59%, r₃ = 14.59%

3. r₁ = 12.27%, r₂ = 13.59%, r₃ = 23.59%

4. r₁ = 15.45%, r₂ = 12.59%, r₃ = 13.59%

Задача 104.

Оценить текущую стоимость облигации с нулевым купоном номинальной стоимостью 10000 руб. и сроком погашения через 3 года. Ставка дисконта r=19%.

Ответы:

1. PV = S(0) = 5934 руб.

2. PV = S(0) = 6934 руб.

3. PV = S(0) = 5034 руб.

4. PV = S(0) = 5934 руб.

Задача 105.

Оценить текущую стоимость облигации (PV) по номинальной стоимости 100 тыс. руб. с купонной ставкой r_k=20%, дисконтом r=12%. Срок погашения 5 лет.

Ответы:

1. PV = S(0) = 128838 руб.

2. PV = S(0) = 138839 руб.

3. PV = S(0) = 99784 руб.

4. PV = S(0) = 112325 руб.

Задача 106.

Оценить текущую стоимость бессрочной облигации, если по ней ежегодно выплачивается доход 10 тыс. руб. Ставка дисконта r=10%.

Ответы:

1. PV = S(0) = 100 тыс. руб.

2. PV = S(0) = 110 тыс. руб.

3. PV = S(0) = 105 тыс. руб.

4. PV = S(0) = 125 тыс. руб.

Задача 107.

Оценить текущую стоимость акции, если каждый год дивиденд равен 100 тыс. руб. Ставка дисконта r=5%.

Ответы:

1. PV = S(0) = 2 млн. руб.

2. PV = S(0) = 2.3 млн. руб.

3. PV = S(0) = 1.9 млн. руб.

4. PV = S(0) = 3 млн. руб.

Задача 108.

Компания начальный дивиденд D=10 тыс. руб. ежегодно наращивает с темпом роста q=3%. Найти текущую стоимость акций компании при ставке дисконта r=8%

Ответы:

1. PV = S(0) = 216 тыс. руб.

2. PV = S(0) = 224 тыс. руб.

3. PV = S(0) = 143 тыс. руб.

4. PV = S(0) = 117 тыс. руб.

Задача 109.( Задача Г.Марковица)

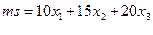Осторожный инвестор формирует портфель из 3 - х ценных бумаг. Средняя эффективность портфеля из 3 - х ценных бумаг равна

где xk – доля средств затраченных на k- ую ценную бумагу.

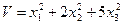Риск сделки, определенный как дисперсия ее эффективности, равен

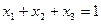При этом предполагается, что выполнено условие баланса

Найти структуру портфеля ценных бумаг, обеспечивающую минимальный риск. Найти соответствующий минимальный риск и соответствующую среднюю эффективность оптимального портфеля.

Ответы:

1. x₁ = 0.588, x₂=0.294, x₃=0.118, V=0.588, m =12.647

2. x₁ = 0.598, x₂=0.284, x₃=0.108, V=0.598, m =12.647

3. x₁ = 0.608, x₂=0.284, x₃=0.108, V=0.597, m =13.647

4. x₁ = 0.388, x₂=0.3294, x₃=0.218, V=0.388, m =10.647

Задача 110. (Задача Д.Тобина)

Инвестор формирует портфель из 4 - х ценных бумаг, одна из которых является государственной безрисковой бумагой. Средняя эффективность портфеля из 4 - х ценных бумаг равна

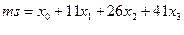где xk – доля средств затраченных на k- ую ценную бумагу, в частности x₀ средств затрачено на безрисковую ценную бумагу.

Риск сделки, определенный как дисперсия эффективности, равен

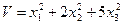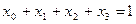При этом предполагается, что выполнено условие баланса

Найти структуру портфеля ценных бумаг, обеспечивающую минимальный риск при фиксированной доходности ms = 11. Найти соответствующий минимальный риск.

Ответы:

1. x₀=0.584, x₁=0.136, x₂=0.171, x₃=0.109, V=0.1365.

2. x₀=0.504, x₁=0.156, x₂=0.191, x₃=0.129, V=0.1565.

3. x₀=0.684, x₁=0.106, x₂=0.101, x₃=0.109, V=0.1265.

4. x₀=0.544, x₁=0.146, x₂=0.181, x₃=0.129, V=0.1365.