Тема №4: Математические основы финансового менеджмента
1. Способы начисления процента
2. Сущность простых и сложных процентов
3. Содержание операций дисконтирования и наращения
4. Учет инфляции в принятии финансовых решений
5. Методы оценки аннуитета
№1
Существует 2 способа определения и начисления процентов:
1) Декурскивный способ начисления процентов – проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставляемого капитала. Декурсивная процентная ставка – это выраженное в процентах отношение суммы начисленного за определенный интервал дохода к сумме имеющейся на начало данного интервала
2) Антисипотивный (предварительный) способ начисления процентов. Проценты начисляются в начале каждого интервала. Сумма процентных денег определятся исходя из наращенной суммы. Процентной ставкой будет выраженное в процентах отношение суммы дохода выплачиваемого за определенный интервал к величине наращенной суммы полученной по истечении этого периода.
№2
Известны две основные схемы дискретного начисления:
· 1. Схема простых процентов – предполагает неизменность базы с которой происходит начисления. Процесс наращения , т.е. определения будущей суммы , определяется по формуле.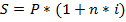 
. P-первоначальная сумма кредита. i-процентная ставка. N-период начисления процента.
· 2. Схема сложных процентов – предполагает что очередной годовой доход исчисляется , не с исходной величины инвестируемого капитала, а с общей суммы включающий так же и раннее начисленные и не востребованные инвестором проценты. В этом случае происходит капитализация процентов , по мере их начисления. База с которой начисляются проценты, все время возрастает. Процесс наращения по сложным процентам реализуются по формуле: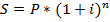 
. Таким образом , в случае ежегодного начисления процента , для лица предоставляющего кредит:
o 1. Более выгодным является схема простых процентов, если срок ссуды менее одного года.
o 2. Более выгодной является схема сложных процентов, если срок ссуды превышает 1 год.
o 3. Обе схемы дают одинаковые результаты , при продолжительности периода один год и однократным начислении, процентов.
№3
Процесс в котором заданы исходная сумма и ставка в финансовых вычислениях называются процессом наращения, искомая величина наращенной суммой , а использованная операцией ставка, ставкой наращения. Процесс в котором заданы , ожидаемая в будущем , к получению сумма и ставка называется процессом дисконтирования , искомая величина приведенной суммой , а использованная операцией ставка – ставка дисконтирования.
Процесс дисконтирования по простым процентам , осуществляется по формуле
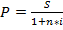
Процесс дисконтирования по сложным процентам, осуществляется по формуле 
.
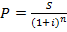№4
Инфляция характеризуется , объяснением национальной валюты и общим повышением цен в стране. Оценка стоимости денежных средств с учетом факторов инфляции, позволяет осуществлять расчеты как в будущем так и настоящей их стоимости с соответствующих инфляционной составляющей.
В основе осуществления этих расчетов лежит формируемая реальная процентная ставка. При оценки будущей стоимости денежных средств с учетом факторов инфляции используется следующая формула:
.
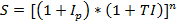Это модель Фишера определяющая реальную процентную ставку с учетом фактора инфляции. TI – это годовой темп инфляции.
Модель Фишера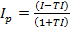 
I – номинальная процентная ставка , выраженная десятичной дробью.
№5
Поток , однонаправленных платежей , с равными интервалами между последовательными платежами в течении определенного количества лет называется аннуитетом или финансовой рентой.
Наиболее распространенной пример аннуитете – это регулярные взносы в пенсионный фонд, выплаты процентов по ценным бумагам и другое.
Аннуитет для которого платежи осуществляется в начале соответствующих интервалов носит название аннуитета при нумерандом. Если платежи осуществляется в конце интервалов – пост нумерандом.
Прямая задача оценки срочного аннуитета пост нумерандо имеет вид:
а – аннуитетный платеж
FM3(i,n) – мультиплицирующий множитель для аннуитета, его значения табулированные.
Образная задача оценки аннуитета постнумерандо имеет вид:
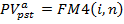
FM4(i,n) – дисконтирующий множитель для аннуитета.