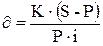Эффективная годовая процентная ставка
Эффективная годовая процентная ставка ( ie ) – это простая процентная ставка, которая начисляется за 1 год и дает такой же результат, что и ставка сложных процентов « j », начисляемая « m » раз в году. Из определения следует:
 |
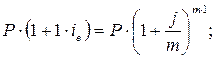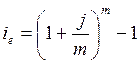отсюда:
| (2.6) |
Эффективная годовая процентная ставка используется для выявления наиболее благоприятных условий для вкладов в банки и получения кредитов.
Пример 2.8. Банки предлагают следующие условия для вкладов:
1й банк – 36% годовых начисляемых по полугодиям (j =0.36; m = 2),
2й банк – 35% годовых начисляемых по кварталам (j = 0.35; m = 4),
3й банк – 34% годовых начисляемых ежемесячно (j = 0.34; m = 12).
Какой банк предлагает наилучшие условия для вкладов?
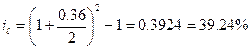Решение данной задачи заключается в нахождении эффективной годовой процентной ставки ( ie ) для каждого банка. Где она выше, там условия для вкладов лучше.
1) Для 1го банка:
 |
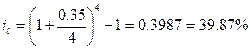2) Для 2го банка:
 |
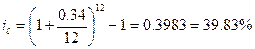3) Для 3го банка:
Самая высокая эффективная, годовая процентная ставка 39,87%, у 2го банка, т.е. значит, он предлагает самые выгодные условия для вкладов.
Пример 2.9. Первый банк дает кредит под 30% годовых при ежеквартальном начислении процентов. Второй банк дает кредит под 29% годовых при ежемесячном начислении процентов. В каком банке выгоднее взять кредит?
Решение:
Кредит выгоднее взять в том банке, где эффективная годовая процентная ставка ниже.
1) 
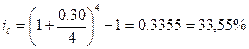Для 1го банка:
 |
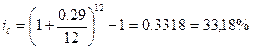2) Для 2го банка:
Ответ: Кредит выгоднее взять во втором банке.
Расчет срока кредита и процентных ставок.
Рассмотрим формулы, используемые для решения задач такого типа на двух примерах.
Пример 2.10. За какой срок первоначальный капитал в 50000 рублей увеличится до 70000 рублей, если на него начисляется 25% годовых:
a) начисление процентов по простой ставке:
b) начисление процентов по ставке сложных процентов:
c) начисление процентов ежемесячно (m=12).
Решая данную задачу, выведем три формулы.
Решение:
a)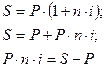 
Для простых процентов
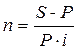 | (2.7) |
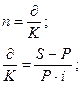Формула для подсчета срока кредита в годах, если нужно срок вычислить в днях, то:
| (2.8) |
| Дано: | Решение: |
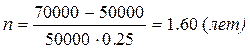 P = 50000 руб. S = 70000 руб. i = 25% = 0,25 | |
| n = ? | Ответ: а) 1,60 лет. |
b)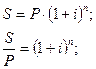 
для сложных процентов:
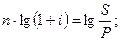От обеих частей берем десятичный логарифм:
 |
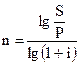| (2.9) |
c)
 |
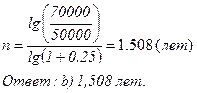Для сложных процентов при начислении процентов « m » раз в году.
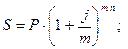
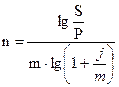 | (2.10) |
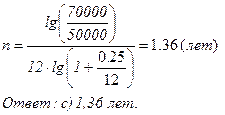
Пример 2.11. Какова должна быть процентная ставка, чтобы первоначальный капитал 40000 рублей достиг 55000 рублей за 2 года? Решить данную задачу для случаев:
a) Проценты простые;
b) Проценты сложные;
c) Начисление процентов ежемесячное.
Решение:
a) Для простых процентов:
 |
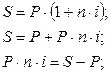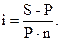 | (2.11) |
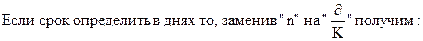
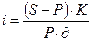 | (2.12) | ||
| Дано: | Решение: | ||
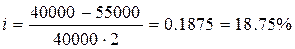 P = 40000 руб. S = 55000 руб. n = 2 года | |||
| i = ? | Ответ: а) 18.75%. | ||
b)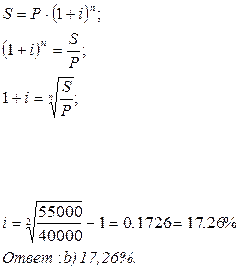 
Для сложных процентов:
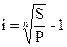 | (2.13) |
c)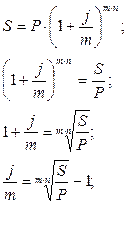 
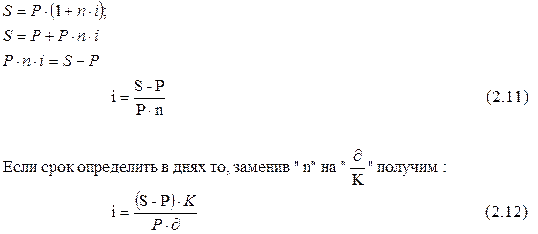Начисление процентов « m » раз в году:
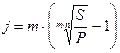 | (2.14) |
 |
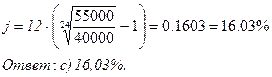Потоки платежей
В кредитном соглашении, как правило, предусматривается не одноразовое погашение всей суммы долга, а определенное количество выплат, распределенных во времени.
Ряд последовательных выплат и поступлений называют потоком платежей.
Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом.
Финансовая рента имеет следующие параметры:
Ø член ренты – величина каждого отдельного платежа;
Ø период ренты – временный интервал между двумя соседними платежами;
Ø срок ренты – время от начала финансовой ренты до конца ее последнего периода;
Ø процентная ставка – ставка, используемая при наращении или дисконтировании платежей;
Ø число платежей в году;
Ø число начислений процентов в году;
Ø моменты платежа внутри периода ренты.
Формулы наращенной суммы.
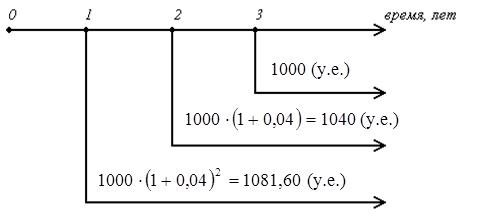
Пример 3.1. Клиент может вносить в банк в конце каждого года 1000 у.е. Какая сумма будет им накоплена на счете через 3 года, если банк платит 4% по депозиту?
Решение:
Первый взнос 1000 у.е. пробудет на счете 2 года и превратится в сумму: 1000∙ (1+0,04)2 = 1081,60 (у.е.)
Второй взнос1000 у.е. пробудет на счете 1 год и превратится в сумму:
1000∙ (1+0,04) = 1040 (у.е.)
На третий взнос проценты не начисляются.
Итого на счете у клиента будет сумма:
1000∙ (1+0,04)0 + 1000∙ (1+0,04)1 + 1000∙ (1+0,04)2 = 3121,60 у.е.
Рассмотрим данную задачу в общем виде. Клиент в конце каждого года вносит в банк вклад « R ». Найти сумму на счете через « n » лет, если банк начисляет сложные проценты по ставке « i ».
S = R∙ (1+i)0 + R∙ (1+i)1 + R∙ (1+i)2 + … + R∙ (1+i)n-1;
S = R∙ [(1+i)0 + (1+i)1 + (1+i)2 + … + (1+i)n-1].
В квадратных скобках сумма членов геометрической прогрессии, используя формулу для ее вычисления, получим:
| (3.1) |
Решим выше приведенный пример по формуле (3.1):
| Дано: | Решение: |
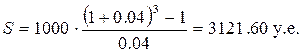 R = 1000 у.е. n = 3 года i = 0,04 = 4% | |
| S = ? | Ответ: 3121.60 y.e. |
Рассмотренный пример финансовой ренты, когда платежи были в конце периода начисления процентов, называется постнумерандо или обычной рентой (Ordinary Annuity).
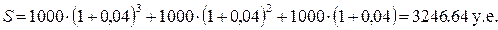Если в указанном примере клиент делает взносы по 1000 у.е. в начале каждого года, то
В общем случае формула имеет вид:
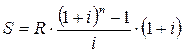 | (3.2) |
Этот вид ренты называется пренумерандо (Annuity Due).
Если начисление процентов производится « m » раз в году, а платежи « p » раз в году, то формула принимает вид:
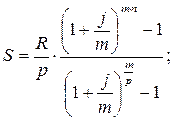 | (3.3) |
(3.3) – расчеты по формуле постнумерандо.
 |
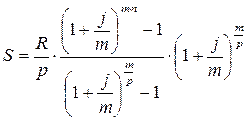| (3.4) |
(3.4) – расчеты по схеме пренумерандо.
Пример 3.2. Раз в квартал делается взнос в банк по схеме пренумерандо в размере 400 у.е. Какая сумма будет на счете через 5 лет, если ставка сложных процентов 8% годовых при ежемесячном начислении процентов:
| Дано: | Решение: |
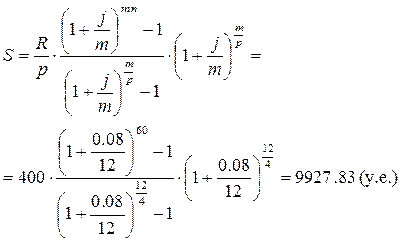 R/p = 400 у.е. p = 4 m = 12 i = 0,08 = 8% n = 5 лет | |
| S = ? | Ответ: 9927,83 y.e. |
Всего же будет заплачено за 5 лет сумма 400 у.е.∙ 20 = 8000 у.е.
На практике встречаются случаи, когда « m » = « р », т.е. количество периодов начисления процентов и число платежей в году одинаково. Тогда в формулах (3.3) и (3.4) вместо « р » ставят « m ».
Расчеты по схеме постнумерандо:
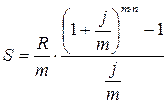
| (3.5) |
Расчеты по схеме пренумерандо:
 |
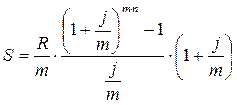| (3.6) |
Пример 3.3. Руководство фирмы считает, что через 5 лет используемое оборудование морально устареет и его нужно будет обновить. Для этой цели фирме нужно накопить 10000 у.е. Каковы должны быть ежемесячные платежи, если процентная ставка 6% годовых при ежемесячном начислении процентов?
| Дано: | Решение: |
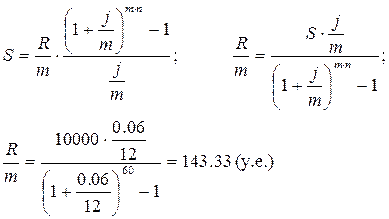 S = 10000 у.е. m = p = 12 j = 0,06 = 6% n = 5 лет | |
| R/m = ? | Ответ: 143.33 y.e. |
Формулы (3.5) и (3.6) используются при решении задач, связанных с регулярными выплатами: формирования инвестиционного, пенсионного, страхового, резервного, накопительного фондов и т.п.