Типовые примеры и методы их решения 2 страница

i I I I I I I I I j_____________

о 1 2 3 4 5 6 7 8 9 n

18 х

Полагая Р = 40 тыс. руб., n = 1,5, m = 2, r⁽²⁾ = 0,34, по фор­муле (58) получим сумму на счете через полтора года:

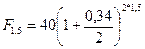тыс. руб.

Поскольку в это время 18 тыс. руб. изымаются, то дальнейшее

наращение осуществляется на сумму [40 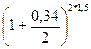-18] тыс.

руб., и, таким образом, через 3 года (n = 3) при закрытии счета господин N получит:

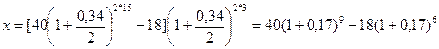= 118,162 тыс. руб.

Заметим, что такое же равенство для нахождения х можно получить, и используя понятие приведенной стоимости, что по­зволяет единообразно решать многие задачи. Дня изложения

нового подхода к решению сформулируем задачу в общем виде. Пусть в банк в конце некоторых периодов начисления сложных процентов помещаются на счет и изымаются со счета некоторые суммы. Найдем приведенные к одному моменту стоимости всех сумм и остатка на счете. Тогда справедливо следующее уравне­ние эквивалентности: сумма приведенных стоимостей всех вкладов равна сумме приведенных стоимостей всех изъятий и приведенной стоимости остатка на счете.

Воспользуемся таким уравнением эквивалентности для ре­шения рассматриваемого примера. Выберем в качестве момента приведения начальный момент времени. В этом случае уравне­ние эквивалентности примет вид:

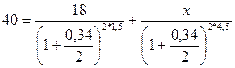
После умножения обеих частей уравнения на множитель

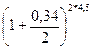= (1 + 0,17) и переноса всех известных слагаемых в

одну часть равенства, а х - в другую, получим:

x=40(1+0,17) -18(1+0,17)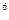

т.е. пришли к такому же выражению для определения х, как и ранее.

В качестве момента приведения можно было выбрать любой момент времени. Так, если взять 4 года 6 месяцев, то уравнение эквивалентности примет вид:

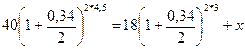
т.е. опять получаем то же самое выражение для определения х.

Пример 2.1.16.На вашем счете в банке лежит сумма в 60 тыс. руб. Банк начисляет сложные проценты по процентной ставке 32% годовых. Вам предлагают войти всем вашим капита­лом в организацию венчурного предприятия. Представленные экономические расчеты показывают, что через 4 года ваш капи­тал возрастет в 3,5 раза. Стоит ли принимать это предложение? Как может повлиять на выбор решения учет фактора риска?

Решение.Оценка данной ситуации может быть сделана либо с позиции будущего, либо с позиции настоящего. В первом слу­чае анализ основан на сравнении двух сумм, получаемых от вложения в рисковое предприятие и в банковское учреждение с гарантированным доходом. Первая сумма равна 60-3,5=210 тыс. руб,, вторая находится по формуле (55):

F_A = 60(1 + 032)⁴ = 182,157 тыс. руб.

Приведенный расчет свидетельствует об экономической вы­годе сделанного вам предложения. Однако при принятии окон­чательного решения необходимо по возможности учесть фактор риска.

Второй вариант анализа основан на дисконтированных оценках с использованием формул (65) и (66). В этом случае процентная ставка в множителе дисконтирования устанавливается инвестором и равна тому относительному размеру дохода, который инвестор хочет или может получить на инвестируемый им капитал.

Определяя процентную ставку в дисконтном множителе, обычно исходят из так называемого безопасного или гарантиро­ванного уровня доходности финансовых инвестиций, который обеспечивается государственным банком по вкладам или при операциях с ценными бумагами. При этом может даваться над­бавка за риск, причем, чем более рисковым считается рассмат­риваемый проект или финансовый контракт, тем больше размер премии за риск. Иными словами, процентная ставка r , исполь­зуемая в дисконтном множителе, будет в этом случае иметь сле­дующий вид:

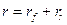
где r 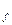- безрисковая доходность; r_r - премия за риск.

Допустим, что финансовый консультант рекомендует оце­нить риск участия в венчурном предприятии путем введения премии в размере 8%. Таким образом, используемая в множите­ле дисконтирования ставка будет равна 40%. Тогда по формуле (65) можно рассчитать приведенную стоимость ожидаемого по­ступления при участии в венчурном предприятии:

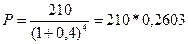= 54,663 тыс. руб.

При таких исходных посылках предложение об участии в венчурном предприятии становится невыгодным. Однако следу­ет иметь в виду, что такой вывод сделан в результате оценки риска путем введения премии в размере 8%. Бели же, например, считать достаточной премию в размере 4%, то по формуле (65) получим:

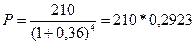= 2100,2923 = 61,383 тыс. руб.,

т.е. предложение об участии в венчурном предприятии стано­вится выгодным.

Пример 2.1.17.Банк начисляет ежеквартально сложные проценты на вклады по номинальной годовой процентной став­ке 32%. Определите в виде простой годовой процентной ставки стоимость привлеченных средств для банка при их размещении: а) на 9 месяцев; б) на год.

Решение,а) Стоимость привлеченных средств можно найти по формуле (23), где через Р обозначена использованная сумма средств; через F-P - проценты, выплаченные за использова­ние суммы Р в течение времени n, a F определяется с помо­щью формулы (58), где п = 0,75, m = 4, r⁽⁴⁾ = 0,32. Итак,

F-P =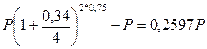

r = 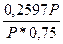= 0,3463, или 34,63% годовых.

Конечно, можно былои сразу применить формулу (81):

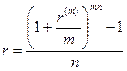, устанавливающую эквивалентность простои

и

ставки rи сложной ставки r ^(m):

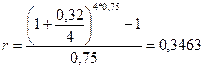
По существу в изложенном предыдущем решении приведена схема вывода этой формулы. б) Полагая n = 1, воспользуемся сразу формулой (81) или, что то же самое в этом случае, формулой (63):

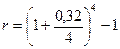= 0,3605 = 36,05%.

Таким образом, относительная стоимость привлеченных средств в этом случае равна эффективной ставке.

Пример 2.1.18.Предприниматель получил в банке кредит на 5 лет по процевтной ставке 28% годовых, при этом банком были удержаны комиссионные в размере 1,4% от величины кредита. Найдите доходность такой финансовой операции для банка в виде эффективной процентной ставки, если банк начисляет еже­годно сложные проценты на исходную сумму кредита. Как из­менится доходность при выдаче кредита на 3 года и на 8 лет?

Решение.Обозначим через Р величину кредита, тогда вели­чина удержанных комиссионных составит 0.014Р, и, следова­тельно, предпринимателю будет выдана сумма Р -0.014Р = 0.986Р. За 5 лет исходная сумма вместе с начислен­ными процентами составит: F₅ = P(l + 0,28)⁵ . Теперь по формуле (64) можно определить доходность финансовой операции для банка в виде эффективной процентной ставки:

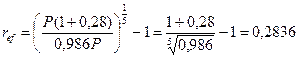
т.е. 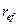= 28,36%, что больше объявленных банком 28% годовых.

Таким образом, удержание комиссионных увеличивает доход­ность финансовой операции для кредитора (банка).

При выдаче кредита на 3 года наращенная сумма составит

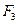=P(1 + 0,28)³. и. следовательно, доходность для банка будет равна:

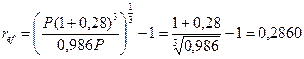
т.е. больше, чем при выдаче кредита на 5 лет.

Аналогичным образом при сроке кредита 8 лет получим:

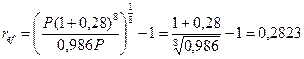
т.е. меньше, чем при выдаче кредита на 5 лет.

Основываясь на рассмотренном примере, можно сделать вы­вод, что при удержании комиссионных увеличение срока креди­та уменьшает доходность финансовой сделки для кредитора. Конечно, если комиссионные не взимаются, то при любом сроке кредита при ежегодном начислении сложных процентов доход­ность такой финансовой сделки в виде годовой эффективной процентной ставки будет постоянной и равна 28%.

Пример 2.1.19.Выдана ссуда под процентную ставку 35% годовых, при этом сразу были взысканы комиссионные в разме­ре 3% от величины ссуды. Определите доходность такой сделки в виде годовой эффективной процентной ставки, если кредитор начисляет простые проценты на исходную величину ссуды и срок ссуды: а) 3 года; б) 6 лет.

Решение,а) Если Р - величина ссуды, то удержанные ко­миссионные составят 0,03Р, и поэтому заемщику будет выдана сумма P- 0,03Р * 0.97Р. Через 3 года заемщик должен возвра­тить сумму F₃ = Р(1 + 3*0,35) = 2,05.Р. Следовательно, по формуле (64) доходность сделки для кредитора составит:

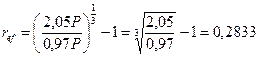или 28,33%.

Если бы комиссионные не взыскивались, то

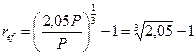= 0,2703, или 27,03%.

Как и следовало ожидать, удержание комиссионных увели­чивает доходность сделки для кредитора.

б) При выдаче ссуды на 6 лет наращенная сумма составит F₆ = Р(1 + 6 *0,35) =3,1Р и поэтому:

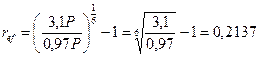или 2137%.

Таким образом, увеличение срока ссуды уменьшает доход­ность сделки для кредитора.

Пример 2.1.20.Вы имеете возможность поместить свои сво­бодные денежные средства в долларах США на полтора года в одном банке на валютном депозите под процентную ставку 16% годовых с ежемесячным начислением сложных процентов или в другом банке эту же сумму поместить на рублевом депозите под процентную ставку 20% годовых с полугодовым начислением сложных процентов. Как вам лучше поступить, если курс по­купки долларов на начало срока - 19 руб. 10 коп., а ожидаемый курс продажи через полтора года - 22 руб. 80 коп.?

Решение.Обозначим имеющееся количество долларов через Р . Помещая их на валютный депозит, через полтора года мож­но получить (согласно формуле (58)):

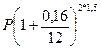= 1,2692 долл. США.

Если же имеющиеся Р долларов обменять на рубли, то в со­ответствии с курсом покупки можно получить 19.1Рруб. Через полтора года наращенная сумма на рублевом депозите составит:

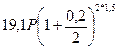=25,4221 руб.,

что при конвертации по ожидаемому курсу продажи даст:

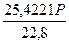= 1,1150долл. США. Сравнивая эту величину с наращенной суммой на валютном депозите, делаем вывод, что луч­ше поместить доллары на валютный депозит.

Пример 2.1.21.На вклад 200 тыс. руб. по истечении 5 лет были начислены сложные проценты по годовой номинальной процентной ставке 28% исходя из ежеквартальной схемы .начис­ления. Определите наращенную сумму после уплаты налога на проценты, если налог на все полученные проценты выплачи­вается один раз в конце срока и ставка налога на проценты равна 15%.

Решение. Полагая Р = 200 тыс. руб., n = 5, m = 4, r⁽⁴⁾ = 0,28, по формуле (58) находим наращенную сумму до уплаты налога:

F₅ = 200 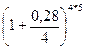= 773,937 тыс. руб.

Сумма налога на проценты составит:

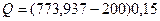= 86,091 тыс. руб.

Следовательно, после уплаты налога наращенная сумма ста­нет равной величине:

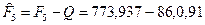= 687,846 тыс. руб. Это значение можно получить и по формуле (101), где

Пример 2.1.22.На вклад в 200 тыс. руб. в течение 5 лет раз в год начислялись сложные проценты по годовой номинальной про­центной ставке 28% исходя из ежеквартальной схемы начисления. Определите итоговую наращенную сумму после уплаты налога на проценты, если налог на проценты уплачивается каждый год путем выделения средств из накапливаемой суммы и ставка налога на проценты равна 15%. Чему равна величина налога за каждый год?

Решение.Используя обозначения предыдущего примера, итоговую наращенную сумму после уплаты налога на проценты находим по формуле (102):

F₅ =200 [13108 - (1,3108 -1) – 0,15]⁵ =645,765 тыс, руб.

Для определения величины налога за каждый год воспользуем­ся рекуррентным соотношением, следующим из формулы (103):

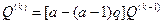, где к = 2,3,...,n. Таким образом,

Q⁽¹⁾ = 200 *(1,3108 -1) * 0,15 = 9,324 тыс. руб.,

Q⁽²⁾ = 9,324 * 1,2642 = 11,787 тыс. руб.,

Q⁽³⁾ = 11,787 * 1,2642 = 14,901 тыс. руб.,

Q⁽⁴⁾ =14,901*1,2642 = 18,838 тыс. руб.,

Q⁽³⁾ = 18,838*1,2642 = 23,815 тыс. руб.

Задачи

2.1.1. Депозит в 40 тыс. руб. положен в банк на 5 лет под процентную ставку 28% годовых. Найдите наращенную сумму, если ежегодно начисляются сложные проценты. Составьте схе­му возрастания капитала по годам.

2.1.2. Сумма 24 тыс. руб. инвестируется под процентную ставку 30% годовых: а) на 4 года; 6) на 10 лет. Найдите нара­щенные суммы при условии ежегодного начисления сложных и простых процентов.

2.1.3. Сделайте сравнительный анализ графиков изменения наращения капитала при реализации схем простых и сложных процентов.

2.1.4. Предприниматель получил в банке ссуду в размере 30 тыс. руб. сроком на 7 лет на следующих условиях: для первых двух лет процентная ставка равна 22% годовых, на следующие три года устанавливается маржа в размере 0,5% и на последую­щие годы маржа равна 0,8%. Найдите сумму, которую предпри­ниматель должен вернуть в банк по окончании срока ссуды при ежегодном начислении сложных процентов.

2.1.5. Банк предоставил ссуду в размере 250 тыс. руб. на 33 месяца под процентную ставку 34% годовых на условиях еже­годного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока при использовании схемы сложных процентов и при использовании смешанной схемы? Какая схема менее выгодна для банка?

2.1.6. Предприниматель взял в банке кредит в размере 90 тыс. руб. под сложную процентную ставку 36% годовых на условиях ежегодного начисления процентов. Через 2 года и 7 месяцев кредит был погашен суммой 201,421 тыс. руб. Какую из двух основных схем начисления процентов использовал банк?

2.1.7. Вы делаете вклад в банк в размере 14 тыс. руб. сроком на 5 лет. Банк начисляет 32% годовых. Какая сумма будет на счете к концу срока, если начисление процентов производится по схеме сложных и простых процентов: а) ежегодно; б) каждые полгода?

2.1.8. Рассчитайте наращенную сумму с исходной суммы в 1 тыс. руб. при размещении ее в банке на условиях начисления простых и сложных процентов, если годовая процентная ставке равна 24%, периоды наращения различны: 30 дней, 150 дней, 210 дней, 1 год, 4 года, 10 лет, 20 лет. Полагать год равным 360 дней. Обсудите полученные результаты.

2.1.9. В банк вложены деньги в сумме 8 тыс. руб. на полтора года под 32% годовых с ежеквартальным начислением сложных процентов. Приведите схему возрастания капитала в конце каж­дого периода. Как изменится итоговая наращенная сумма при ежемесячном начислении сложных процентов? Какой вывод можно сделать о частоте начисления сложных процентов?

2.1.10 Клиент поместил в банк 100 тыс. руб. на 5 лет под процентную ставку 36% годовых. Определите наращенную за это время сумму при начислении сложных процентов: а) еже­годно; б) по полугодиям; в) ежеквартально; г) ежемесячно; д) еженедельно; е) ежедневно. Полагать в году 360 дней.

2.1.11. Банк предоставил ссуду в размере 150 тыс. руб. на 39 месяцев под процентную ставку 30% годовых на условиях еди­новременного возврата основной суммы долга и начисленных сложных процентов. Проанализируйте, какую сумму предстоит вернуть банку при различных вариантах и схемах начисления процентов: а) годовое; б) полугодовое; в) квартальное.

2.1.12. Определите время, за которое происходит удвоение первоначальной суммы при начислении простых и сложных процентов, если процентная ставка равна: а) 5%; б) 10%; в) 15%; г) 25%; д) 50%; е) 75%; ж) 100%.

2.1.13. На вклад в конце каждого полугодия начисляются сложные проценты по номинальной годовой процентной ставке 20%. За какой срок первоначальный капитал увеличится в четы­ре раза? Как изменится результат, если сложные проценты на­числяются ежемесячно?

2.1.14. За какой срок исходная сумма 20 тыс. руб. возрастет до 60 тыс. руб., если сложные проценты по процентной ставке 28%

дгрдовых начисляются: а) ежегодно; б) ежеквартально; в) ежеме-«чир?

2.1.15. Вы имеете 10 тыс. руб. и хотели бы удвоить эту сум-Через пять лет. Каково минимально приемлемое значение сложной процентной ставки при ежегодном начислении процентов? Сравните результат, полученный по точной формуле, с ре-ультатом, полученным с помощью "правила 72-х".

2.1.16. Вкладчик хотел бы за 4 года удвоить сумму, поме­щаемую в банк на депозит. Какую годовую номинальную про­центную ставку должен предложить банк при начислении слож­ных процентов ежеквартально?

2.1.17. Господин N хочет поместить в банк 8 тыс. руб., чтобы через 3 года получить 12 тыс. руб. Какова должна быть годовая номинальная процентная ставка при начислении сложных про­центов: а) каждые полгода; б) каждый квартал?

2.1.18. Какие условия предоставления кредита при начисле­нии сложных процентов по процентной ставке более выгодны банку: а) 29% годовых, начисление ежеквартальное; 6) 30% го­довых, начисление полугодовое?

2.1.19. Вы имеете возможность получить кредит либо на ус­ловиях 32% годовых с ежемесячным начислением сложных процентов, либо на условиях 33% годовых с ежеквартальным начислением сложных процентов. Какой вариант предпочти­тельнее, если выплата процентов будет сделана единовременно вместе с погашением кредита?

2.1.20. Рассчитайте эффективную годовую процентную став­ку при различной частоте начисления сложных процентов, если номинальная процентная ставка равна 20% годовых. Сравните между собой полученные результаты.

2.1.21. В долг на 3 года 6 месяцев предоставлена сумма 8 тыс. руб. с условием возврата 20 тыс. руб. Найдите эффектив­ную процентную ставку в этой финансовой сделке.

2.1.22. Предприниматель инвестировал 60 тыс. руб, и полу­чил через 140 дней 75 тыс, руб. Определите доходность этой операции в виде эффективной процентной ставки на базе: а) 360 дней; б) 365 дней.

2.1.23. Определите номинальную годовую процентную ставку, если эффективная ставка равна 30% и сложные проценты начис­ляются: а) ежеквартально; б) ежемесячно.

2.1.24. Каковы будут эквивалентные номинальные годовые процентные ставки с начислением сложных процентов по полу­годиям и ежемесячно, если соответствующая им эффективная ставка равна 26%?

2.1.25. Из какого капитала можно получить 15 тыс. руб. че­рез 4 года наращением сложными процентами по процентной ставке 24% годовых, если наращение осуществлять: а) ежегод­но; б) по полугодиям; в) ежемесячно? Чему равен дисконт?

2.1-26. Наращенная к концу седьмого года сумма составит 240 тыс. руб. Найдите ее современное значение, если начисля­ются сложные проценты: а) по полугодиям по процентной став­ке 30% годовых; б) ежеквартально по процентной ставке 40% годовых.

2.1.27. Какую сумму необходимо поместить в банк под сложную процентную ставку 30% годовых, чтобы накопить 50 тыс. руб.: а) за 6 лет при ежегодном начислении процентов; б) за 4 года при ежемесячном начислении процентов?

2.1.28. Определите современную ценность 40 тыс. руб., если: а) эта сумма будет получена через 5 лет 3 месяца; б) эта сумма была получена 3 года 6 месяцев назад; в) эта сумма получена в настоящий момент времени. Учесть возможность помещения денег на депозит под сложную процентную ставку 36% годовых.

2Л .29. Банк начисляет ежеквартально сложные проценты по годовой номинальной процентной ставке 32%. Определите со­временную ценность 15 тыс. руб,, если: а) эта сумма была по­мещена на депозит в банке 3 года 2 месяца назад; б) эта сумма будет помещена на депозит в банке через 10 месяцев.

2.1.30. Свободные денежные средства помещены в банк под сложную процентную ставку 40% годовых на условиях ежегод­ного начисления процентов. Через 3 года и 10 месяцев счет был закрыт и получена сумма в размере 36,587 тыс. руб. Определите величину наращенной суммы, которая была бы получена при закрытии счета через 2 года и 3 месяца, если банк начисляет проценты по смешанной схеме.

2.1.31. На вашем счете в банке 8 тыс, руб. Банк платит 22% го­довых, Вам предлагают принять участие всем вашим капиталом в некоторой финансовой сделке. Представленные экономические расчеты показывают, что в случае согласия через пять лет ваш ка­питал возрастет в 2,9 раза. Стоит ли принимать это предложение? Оцените ситуацию с позиции будущего и с позиции настоящего. Как может повлиять на выбор решения учет фактора риска?

2.1.32. Какая сумма предпочтительнее при сложной процент­ной ставке 29% годовых: 100 тыс. руб. сегодня или 700 тыс. руб. через 8 лет?

2.1.33. Что выгоднее: получить 4,6 тыс. руб. через 4 года или 5,2 тыс. руб. через 5 лет, если можно поместить деньги на депозит под сложную процентную ставку 16% годовых? Оцените ситуацию с позиции будущего и с позиции настоящего.

2.1.34. Определите, под какую сложную процентную ставку можно поместить деньги на депозит, если 10 тыс. руб. сейчас будут эквивалентны 37,129 тыс. руб. через 5 лет. Как изменится ответ, если банк начисляет сложные проценты ежеквартально?

2.1.35. За взятые в долг деньги под сложную процентную ставку 35% годовых должник обязан уплатить кредитору 30 тыс. руб. 1 июля 1997 г. Какую сумму необходимо уплатить должни­ку, если он вернет долг: а) 1 января 1997 г.; б) 1 января 1998 г.; в) 1 июля 1999 г.?

2.1.36. Клиент поместил в банк 25 тыс. руб. на условиях на­числения сложных процентов по процентной ставке 30% годо­вых. Через 1 год 9 месяцев клиент снял со счета 8 тыс. руб., еще через 3 года положил на свой счет 4 тыс. руб., а после этого че­рез 2 года 3 месяца он закрыл счет. Определите сумму, получен­ную клиентом при закрытии счета.

2.1.37. Господин N поместил в банк 30 тыс. руб. на условиях начисления каждый квартал сложных процентов по годовой но­минальной процентной ставке 32%. Через 3 года 3 месяца гос­подин N снял со счета 12 тыс. руб., еще через 1 год 6 месяцев положил на свой счет 8 тыс. руб., а после этого через 15 месяцев он закрыл счет. Определите сумму, полученную господином N при закрытии счета.

2.1.38. Фирме нужно накопить 2 млн долл., чтобы через 10 лет приобрести здание под офис. Наиболее безопасным способом накопления является приобретение безрисковых государствен­ных ценных бумаг, генерирующих годовой доход по ставке 8% при полугодовом начислении процентов. Каким должен быть первоначальный вклад фирмы?

2.1.39. У вас есть возможность выбора между получением 30 тыс. руб. через год или 72 тыс. руб. через 6 лет. Каков ваш вы­бор, если есть возможность поместить деньги в банк под слож­ную процентную ставку: а) 12%; б) 20%? А если нет возможно­сти инвестирования куда-либо денег или вы не хотите восполь­зоваться такой возможностью?

2.1.40. Вкладчик положил в банк два года назад 16 тыс. руб. на условиях начисления каждый квартал сложных процентов по годовой номинальной процентной ставке 28%. Полгода назад вкладчик снял со счета 12 тыс. руб., а через 3 года после этого он положил 10 тыс. руб. Еще через полтора года вкладчик по­ложил такую сумму, что на его счете еще через полгода оказа­лось 80 тыс. руб. Определите, какую сумму вкладчик положил

последний раз.

2.1.41. Вкладчик открыл счет в банке, положив некоторую сумму денег, Такую же по величине сумму он добавлял на свой счет еще три раза: через 1 год 6 месяцев, 2 года 6 месяцев и 4 года после открытия счета. Через 5 лет на счете вкладчика было 60 тыс. руб. Какую сумму вносил вкладчик каждый раз, если банк начисляет сложные проценты каждые полгода по годовой номи­нальной процентной ставке 30%?

2.1.42. Предприниматель взял в банке кредит на сумму 200 тыс. руб. на условиях начисления сложных процентов по процентной ставке 25% годовых. Через 2 года он вернул банку 120 тыс. руб., но еще через год взял кредит в сумме 60 тыс. руб. Через 3 года после этого предприниматель вернул полностью полученные кредиты. Какую сумму предприниматель при этом выплатил банку?

2.1.43. Определите, какую сумму необходимо поместить в банк, начисляющий ежеквартально сложные проценты по годо­вой номинальной процентной ставке 36%, чтобы иметь возмож­ность снять через 9 месяцев 10 тыс. руб. и еще 20 тыс. руб. через 18 месяцев после этого.

2.1.44. Предприниматель приобрел оборудование стоимо­стью 400 тыс. руб. в кредит под сложную процентную ставку 20% годовых. Через 2 года 6 месяцев он уплатил 250 тыс. руб., а еще через год полностью погасил долг. Определите, какую сум­му предприниматель при этом выплатил.

2.1.45. Господин N приобрел автомобиль стоимостью 140 тыс. руб. в кредит под сложную процентную ставку 30% годовых. Он выплатил в момент покупки 80 тыс. руб., а осталь­ной долг обязался выплатить в течение двух лет равными упла­тами по полугодиям (первая уплата - через полгода с момента покупки). Чему равна каждая уплата?

2.1.46. Строительная фирма продает квартиры стоимостью 450 тыс, руб. в кредит под сложную процентную ставку 25% годовых. Эта же фирма учредила банк, аккумулирующий сред­ства на строительство квартир и выплачивающий по помещен-

175ным в него деньгам сложные проценты по процентной ставке 25% годовых. Господин N внес в этот банк некоторую сумму за 3 года до приобретения квартиры, такую же сумму - в момент приобретения квартиры, еще 70 тыс. руб. - через 2 года и 120 тыс. руб. - через 3 года с момента приобретения квартиры, погасив тем самым свой долг полностью. Определите, какие суммы господин N вносил в банк до и в момент приобретения квартиры.

2.1.47. Строительная фирма продает квартиры стоимостью 520 тыс. руб. в кредит под сложную процентную ставку 20% годовых. Эта же фирма учредила банк, аккумулирующий сред­ства на строительство квартир и выплачивающий по помещен­ным в него деньгам сложные проценты по процентной ставке 20% годовых. Господин N внес в этот банк 100 тыс. руб. за год до получения квартиры и еще 150 тыс. руб. - через 2 года после получения квартиры. Еще через год после этого он внес некото­рую сумму, а еще через год погасил долг, внеся 300 тыс. руб. Определите, какую сумму господин N внес в банк через год по­сле получения квартиры.

2.1.48. Банк начисляет ежемесячно сложные проценты на вклады по номинальной годовой процентной ставке 30%. Опре­делите в виде простой годовой процентной ставки стоимость привлеченных средств для банка при их размещении: а) на 1 ме­сяц; б) на 8 месяцев; в) на год.

2.1.49. Вкладчик помещает в банк 20 тыс. руб. на 3 года под номинальную процентную ставку 36% годовых с ежекварталь­ным начислением сложных процентов. В конце каждого года господин N расходует третью часть наращенной к этому момен­ту суммы. Определите величину наращенной суммы в конце третьего года после осуществления всех расходов.

2.1.50. Господин N помещает в банк 30 тыс. руб. на 4 года под номинальную процентную ставку 38% годовых с полугодовым начислением сложных процентов. В конце каждого года господин N расходует часть наращенной к этому моменту суммы: в конце первого года - четвертую часть, в конце второго года - третью часть, в конце третьего и четвертого - соответственно вторую и четвертую части. Определите величину наращенной суммы в конце четвертого года после осуществления всех расходов. Изме­нится ли ответ, если расходуемые части наращенных сумм будут образовывать такой порядок: