Чем меньше процентная ставка, тем
ТЕСТЫ ПО ДИСЦИПЛИНЕ
«ФИНАНСОВАЯ МАТЕМАТИКА»
1. Принцип неравноценности денег заключается в том, что:
1) A – деньги обесцениваются со временем;
2) B – деньги приносят доход;
3) C – равные по абсолютной величине денежные суммы, относящиеся к различным моментам времени, оцениваются по-разному;
4) D – "сегодняшние деньги ценнее завтрашних денег".
2. Финансово-коммерческие расчеты используются для:
1) A – определения выручки от реализации продукции.
2) B – расчета кредитных операций.
3) C – расчета рентабельности производства.
4) D – расчета доходности ценных бумаг.
3. Подход, при котором фактор времени играет решающую роль, называется:
1) A – временной;
2) B – статический;
3) C – динамический;
4) D – статистический.
4. Проценты в финансовых расчетах:
1) A – это доходность, выраженная в виде десятичной дроби;
2) B – это абсолютная величина дохода от предоставления денег в долг в любой его форме;
3) C – показывают, сколько денежных единиц должен заплатить заемщик за пользование в течение определенного периода времени 100 единиц первоначальной суммы долга;
4) D – это %.
5. Процентная ставка – это:
1) A – относительный показатель, характеризующий интенсивность начисления процентов;
2) B – абсолютная величина дохода от предоставления денег в долг в любой его форме;
3) C – ставка, зафиксированная в виде определенного числа в финансовых контрактах;
4) D – отношение суммы процентных денег к величине ссуды.
6. В качестве единицы времени в финансовых расчетах принят:
1) A – год;
2) B – квартал;
3) C – месяц;
4) D – день.
7. Наращение – это:
1) A – процесс увеличения капитала за счет присоединения процентов;
2) B – базисный темп роста;
3) C – отношение наращенной суммы к первоначальной сумме долга;
4) D – движение денежного потока от настоящего к будущему.
8. Коэффициент наращения – это:
1) A – отношение суммы процентных денег к величине первоначальной суммы;
2) B – отношение наращенной суммы к первоначальной сумме;
3) C – отношение первоначальной суммы к будущей величине денежной суммы;
4) D – отношение процентов к процентной ставке.
9. Виды процентных ставок в зависимости от исходной базы:
1) A – постоянная, сложная;
2) B – простая, переменная;
3) C – простая, сложная;
4) D – постоянная, переменная.
10. Фиксированная процентная ставка – это:
1) A – ставка, неизменная на протяжении всего периода ссуды;
2) B – ставка, применяемая к одной и той же первоначальной сумме долга;
3) C – ставка, зафиксированная в виде определенного числа в финансовых контрактах;
4) D – отношение суммы процентных денег к величине ссуды.
11. Наращение – это:
1) A – процесс увеличения капитала за счет присоединения процентов;
2) B – базисный темп роста;
3) C – отношение наращенной суммы к первоначальной сумме долга;
4) D – движение денежного потока от настоящего к будущему.
12. Формула простых процентов:
1) A – FV = PV • i • n
2) B – FV = PV(1 + i)n
3) C – FV = PV(1 + ni)
4) D – FV = PV(1 + i)
13. Простые проценты используются в случаях:
1) A – реинвестирования процентов;
2) B – выплаты процентов по мере их начисления;
3) C – краткосрочных ссуд, с однократным начислением процентов;
4) D – ссуд, с длительностью более одного года.
14. Точный процент – это:
1) A – капитализация процента;
2) B – коммерческий процент;
3) C – расчет процентов, исходя из продолжительности года в 365 или 366 дней;
4) D – расчет процентов с точным числом дней финансовой операции.
15. Точное число дней финансовой операции можно определить:
1) A – по специальным таблицам порядковых номеров дней года;
2) B – используя прямой счет фактических дней между датами;
3) C – исходя из продолжительности каждого целого месяца в 30 дней;
4) D – считая дату выдачи и дату погашения ссуды за один день.
16. Французская практика начисления процентов:
1) A – обыкновенный процент с приближенным числом дней финансовой операции;
2) B – обыкновенный процент с точным числом дней финансовой операции;
3) C – точный процент с точным числом дней финансовой операции;
4) D – точный процент с приближенным числом дней финансовой операции.
17. Германская практика начисления процентов:
1) A – обыкновенный процент с приближенным числом дней финансовой операции;
2) B – обыкновенный процент с точным числом дней финансовой операции;
3) C – точный процент с точным числом дней финансовой операции;
4) D – точный процент с приближенным числом дней финансовой операции.
18. Английская практика начисления процентов:
1) A – обыкновенный процент с приближенным числом дней финансовой операции;
2) B – обыкновенный процент с точным числом дней финансовой операции;
3) C – точный процент с точным числом дней финансовой операции;
4) D – точный процент с приближенным числом дней финансовой операции.
19. Расчет наращенной суммы в случае дискретно изменяющейся во времени процентной ставки по схеме простых процентов имеет следующий вид:
1) A – FV = PV (1 + Σnкiк)
2) B – FV = PV Σ (1 + nкiк)
3) C – FV = PV (1 + n1i1)(1 + n2i2) : (1 + nкiк)
4) D – FV = PV (1 + n iк)
20. Срок финансовой операции по схеме простых процентов определяется по формуле:
1) A – n = I / (PV • i)
2) B – n = [(FV - PV) / (FV • t)] i
3) C – t = [(FV - PV) / (PV • i)] T
4) D – n = [(FV - PV) / (FV • t)] T
21. Если в условиях финансовой операции отсутствует простая процентная ставка, то:
1) A – этого не может быть;
2) B – ее можно определить по формуле i = [(FV - PV) / (PV • t)]•T
3) C – ее невозможно определить;
4) D – ее можно определить по формуле i = Σ процентных чисел / дивизор .
22. Формула сложных процентов:
1) A – FV = PV(1 + ni)
2) B – FV = PV(1 + t / T • i)
3) C – FV = PV(1 + i)n
4) D – FV = PV(1 + ni)(1 + i)n
23. Начисление по схеме сложных процентов предпочтительнее:
1) A – при краткосрочных финансовых операциях;
2) B – при сроке финансовой операции в один год;
3) C – при долгосрочных финансовых операциях;
4) D – во всех вышеперечисленных случаях.
24. Чем больше периодов начисления процентов:
1) A – тем медленнее идет процесс наращения;
2) B – тем быстрее идет процесс наращения;
3) C – процесс наращения не изменяется;
4) D – процесс наращения предсказать нельзя.
25. Номинальная ставка – это:
1) A – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год;
2) B – отношение суммы процентов, выплачиваемых за фиксированный отрезок времени, к величине ссуды;
3) C – процентная ставка, применяется для декурсивных процентов;
4) D – годовая ставка, с указанием периода начисления процентов.
26. Формула сложных процентов с неоднократным начислением процентов в течение года:
1) A – FV = PV(1 + i) m • n
2) B – FV = PV(1 + j / m) m • n
3) C – FV = PV / m • (1 + i) n / m
4) D – FV = PV(1 + i • m) m • n
27. Эффективная ставка процентов:
1) A – не отражает эффективности финансовой операции;
2) B – измеряет реальный относительный доход;
3) C – отражает эффект финансовой операции;
4) D – зависит от количества начислений и величины первоначальной суммы.
28. Формула сложных процентов с использованием переменных процентных ставок:
1) A – FV = PV(1 + i1) n1 (1 + i2) n2 … (1 + ik) nk
2) B – FV = PV(1 + nkik)
3) С – FV = PV(1 + n1i1 • n2i2 • … • nkik) nk
4) D – FV = PV(1 + in)(1 + i)
29. В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием:
1) A – общего метода;
2) B – эффективной процентной ставки;
3) C – смешанного метода;
4) D – переменных процентных ставок.
30. Смешанный метод расчета:
1) A – FV = PV(1 + i)а + в
2) B – FV = PV(1 + i)а (1 + вi)
3) C – FV = PV(1 + авi)n
4) D – FV = PV(1 + i)а (1 + i)в
31. Непрерывное начисление процентов – это:
1) A – начисление процентов ежедневно;
2) B – начисление процентов ежечасно;
3) C – начисление процентов ежеминутно;
4) D – начисление процентов за нефиксированный промежуток времени.
32. Если в условиях финансовой операции отсутствует ставка сложных процентов, то:
1) A – ее определить нельзя;
2) B – 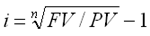
3) C – i = ln(FV / PV) / ln(1 + n)
4) D – i = lim(1 + j / m)m
5) E – i = (1 + j / m)m - 1
33. Дисконтирование – это:
1) A – процесс начисления и удержания процентов вперед;
2) B – определение значения стоимостной величины на некоторый момент времени при условии, что в будущем она составит заданную величину;
3) C – разность между наращенной и первоначальной суммами.
34. Банковский учет – это учет по:
1) A – учетной ставке;
2) B – процентной ставке;
3) C – ставке рефинансирования;
4) D – ставке дисконтирования.
35. Антисипативные проценты – это проценты, начисленные:
1) A – с учетом инфляции;
2) B – по учетной ставке;
3) C – по процентной ставке.
36. Дисконтирование по сложным процентам осуществляется по формуле:
1) A – PV = FV(1 + i) -n
2) B – PV = FV(1 + i) -1
3) C – PV = FV(1 - d) n
4) D – PV = FV(1 + i) n
37. Дисконтирование по простой учетной ставке осуществляется по формуле:
1) A – PV = FV(1 - d) n
2) B – PV = FV(1 - d) -n
3) C – PV = FV(1 - nd)
4) D – PV = FV(1 + nd) -1
Чем меньше процентная ставка, тем
1) A – выше современная величина;
2) B – ниже современная величина;
3) C – на современную величину это не оказывает влияния.
39. Какой вид дисконтирования выгоднее для векселедержателя:
1) A – математическое дисконтирование;
2) B – банковский учет;
3) C – разница отсутствует.
40. Поток платежей - это:
1) A – рост инвестированного капитала на величину процентов;
2) B – распределенные во времени выплаты и поступления;
3) C – перманентное обесценивание денег;
4) D – платеж в конце периода.
41. Вечная рента - это:
1) A – рента, подлежащая безусловной выплате;
2) B – рента с выплатой в начале периода;
3) C – рента с бесконечным числом членов;
4) D – рента с неравными членами.
42. Аннуитет - это:
1) A – частный случай потока платежей, когда члены потока только положительные величины;
2) B – частный случай потока платежей, когда число равных временных интервалов ограничено;
3) C – частный случай потока платежей, когда члены равны и имеют одинаковую направленность, а периоды ренты одинаковы.
43. Наращенная величина годовой постоянной обычной ренты определяется по формуле:
1) A – 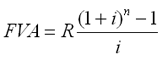
2) B – FVA = R (1 + i)n - 1
3) C – 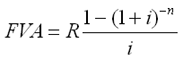
4) D – 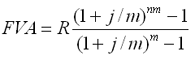
44. Наращенная сумма ренты пренумерандо рассчитывается по формуле:
1) A – 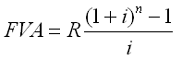
2) B – 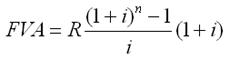
3) C – 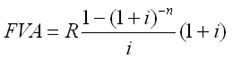
45. Современная величина годовой обычной ренты определяется по формуле:
1) A – 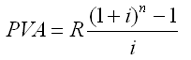
2) B – 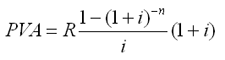
3) C – 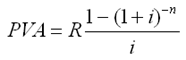
46. Для определения члена ренты необходимо знать:
1) A – наращенную сумму;
2) B – первоначальную сумму;
3) C – первоначальную и наращенную сумму;
4) D – только процентную ставку и срок ренты.
47. Для оценки бессрочного аннуитета не имеет смысла определение:
1) A – современной величины аннуитета;
2) B – наращенной величины аннуитета;
3) C – члена ренты.
48. Нерегулярные потоки платежей характеризуются присутствием нерегулярного параметра:
1) A – периода ренты;
2) B – размера платежа;
3) C – процентной ставки.
49. Уровень инфляции показывает:
1) А – во сколько раз выросли цены;
2) В – во сколько раз цены снизились;
3) С – на сколько процентов цены возросли.
50. Расчет уровня инфляции за период осуществляется:
1) А – по простым процентам;
2) В – по сложным процентам;
3) С – по смешанному методу.
51. Если уровень инфляции ниже процентной ставки, то это:
1) А – уменьшение первоначальной денежной суммы;
2) В – рост реальной денежной суммы;
3) С – роста денежной суммы не будет.
52. Реальная доходность финансовой операции определяется:
1) А – с использованием реальной ставки процентов;
2) В – с использованием номинальной ставки процентов;
3) С – с использованием эффективной ставки.
