Номинальная процентная ставка. Эквивалентные номинальные процентные ставки Эффективная годовая процентная ставка

Номинальная процентная ставка r^(m), которая является годовой, используется для расчетов, для фиксирования в договорах, если в договоре указывается количество периодов начисления в году (m). В этих обозначениях величина наращенного капитала за n лет при m-кратном начислении процентов по сложной процентной ставке равна:

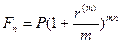, где m – количество начислений процентов за год.

Годовая эффективная ставка r_ef используется для сравнительного анализа эффективности контрактов, является универсальным показателем для любой схемы начисления. Ее использование связано с тем, что различные финансовые контракты могут содержать различные схемы начисления процентов и обычно в этих контрактах оговаривается номинальная процентная ставка обычно годовая, которая не отражает реальной эффективности сделки и не может быть использована для сопоставлений. Таким образом, эффективная ставка измеряет реальный относительный доход, который получает кредитор в целом за год. Иначе говоря, эффективная ставка показывает, какую годовую ставку сложных процентов необходимо установить, чтобы получить такой же финансовый результат, как и при m-разовом начислении процентов в году по ставке r^(m)/m. r_ef рассчитывается из уравнения r_ef =(1+r^(m)/m)^m-1. Эта формула получена из условия, что равенство наращенных сумм будет обеспечено в том случае, если равны первоначальные суммы Р, периоды наращения n и множители наращения:

.

Пример 1. Предприниматель может получить ссуду а) либо на условиях ежемесячного начисления процентов из расчета 26% годовых, б) либо на условиях полугодового начисления процентов из расчета 27% годовых. Какой вариант предпочтительнее?

Решение. Относительные расходы предпринимателя по обслуживанию ссуды могут быть определены с помощью расчета эффективной годовой процентной ставки – чем она выше, тем больше уровень расходов.

Для варианта а) r_ef=(1+0,26/12)-1=0,2933;

Для варианта б) r_ef=(1+0,27/2)-1=0,2882.

Ответ. Таким образом, вариант б) является более предпочтительным для предпринимателя. Отметим, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель эффективная ставка, а она зависит лишь от номинальной ставки и количества начислений.

Понимание роли эффективной процентной ставки важно для финансового менеджера. Можно показать, что при m>1 справедливо неравенство r_ef > r, что следует и из финансовых соображений.

В финансовых соглашениях не имеет значения, какую ставку указывать, так как использование как одной, так и другой дает одну и ту же наращенную сумму с любой точность приближения. В США в практических расчетах применяют номинальную ставку. В европейских странах вначале определяют эффективную ставку и затем пользуются формулой F_n=P(1+r_ef)ⁿ.

Если в контракте указаны эффективная годовая процентная ставка и число начислений сложных процентов, то номинальная процентная ставка находится из формулы:

r^(m)=m[(1+r_ef)^1/m-1].

Пример 2. Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно.

Решение. r⁽¹²⁾=12[(1+0,18)^1/12-1]=0,1667, или 16,67%.

Если две номинальные годовые процентные ставки определяют одну и ту же эффективную ставку, то они называются эквивалентными. Верно следующее равенство:

.

Пример 3. Каковы будут эквивалентные номинальные годовые процентные ставки с начислениями по полугодиям и ежеквартально, если соответствующая им эффективная годовая процентная ставка равна 20%?

Решение. Используя формулу, получим: r⁽²⁾=2[(1+0,2)^1/2-1]=0,1909, r⁽⁴⁾=4[(1+0,2)^1/4-1]=0,1865.

Операции дисконтирования

Процесс определения текущей стоимости денег называется дисконтированием.

Наиболее распространенное применение дисконтирования:
1) авансовое удержание с заемщика процентов в момент выдачи ссуды, т.е. до наступления срока ее погашения; 2) учет векселей в банке, когда банк, принимая вексель от предъявителя, выдает ему обозначенную на векселе сумму до срока его погашения. При этом банк удерживает в свою пользу проценты (дисконт) от суммы векселя за время, оставшееся до срока гашения; 3) оценка облигаций путем дисконтирования будущих купонных платежей, а также оценка акций на основе использования модели дисконтирования дивидендов.

Выделяют два вида дисконтирования – математическое дисконтирование (приведение по вкладу) и банковский учет (приведение по платежу).

Математическое дисконтирование определяет современное или приведенное значение Р на некоторый момент времени T, которое соответствует заданному значению F в другой момент времени t. Таким образом, математическое дисконтирование – это формула сравнения денежных сумм в любые моменты времени. Можно еще определить математическое дисконтирование как приведение по вкладу Р – это такой подход к расчету искомой предшествующей суммы Р, который дает сумму F (известную к началу расчета) при начислении процентов (простых или сложных) через n периодов. В этом случае за базовую величину, то есть за 100% принимается размер вклада Р.

Величину Р, найденную с помощью процесса дисконтирования, называют в зависимости от контекста приведенной (современной, текущей, капитализированной) стоимостью.

Приведем некоторые из формул математического дисконтирования.

1. Дисконтированное значение будущей суммы вклада по простой процентной ставке равно:

(1),

где r – простая годовая процентная ставка;

n – период начисления процентов;

k_D- коэффициент дисконтирования (приведения), равный . Он показывает, какую долю составляет Р в величине F при простой процентной ставке.

2. Дисконтированное значение будущей суммы вклада по сложной процентной ставке равно:

(2),

где r_с – сложная процентная ставка за единичный период начисления;

n – число периодов начисления процентов;

k_DC- коэффициент дисконтирования, равный . Он показывает, какую долю составляет Р в величине F при сложной процентной ставке.

Формулы (1) и (2) используются в частности для сравнения потоков платежей и при расчете стоимости облигаций и прочих ценных бумаг.

Пример 1. Из какого капитала можно получить 3,4 млн. руб. через 3 года наращения по простым процентам при ставке 12%?

Решение. Р=3,4/ (1*30,12)=2,5 млн. руб. Дисконт=Р₂-Р₁=F-P=3,4-2,5=0,9 млн. руб.

Пример 2. Через полгода после заключения финансового соглашения о получении кредита должник обязан заплатить 2,14 тыс. руб. Какова первоначальная величина кредита, если он выдан под 14% годовых и начисляются обыкновенные проценты с приближенным числом дней?

Решение. Д=F-P=2,14-2=0,14 т.р.

Банковское дисконтирование или приведение по платежу (второй подход) состоит в том, что неизвестен размер платежа, к которому придем при удержании с конечной суммы F за срок n. В этом случае за 100% берется будущая сумма F.

Формула дисконтирования приведением по платежу по простым процентам: P_n=F-n*d*F=F(1-nd), где d – учетная ставка, которая фиксирует процентное или долевое уменьшение суммы F на один период назад.

Формула дисконтирования приведением по платежу по сложным процентам: P_n=F(1-d)ⁿ.

Банковский учетзаключается в покупке денежных обязательств банком. Поэтому далее в задачах будет использовано понятие векселя. Вексель– это долговая расписка, содержащая обязательство выплатить определенную денежную сумму (номинал векселя F) в конкретный срок. Вексель может быть простым, переводным, коммерческим, казначейским и т.д. Чаще всего работа с векселем – это принятие векселя к погашению. Учет векселя означает оплату векселя с дисконтом, т.е. со скидкой с его номинала. Дисконт представляет собой проценты, начисленные за время n от дня дисконтирования до дня погашения векселя на сумму F, подлежащую оплате в конце срока. Чем выше значение дисконтной ставки, тем большую сумму удерживает банк в свою пользу. Вексель, допускающий участие третьих лиц, называется переводным или траттой. Учет векселя чаще всего осуществляется способом: приближенное число дней в году (360) и точное число дней в периоде от момента учета векселя до момента погашения (365/360). Приведем некоторые из формул банковского учета, содержащие дисконт.

Для простой учетной ставки:

1. Если срок n от даты учета до даты погашения составляет часть года, то дисконт определяется по формуле где

d –относительная величина годовой учетной ставки;

t- период начисления в днях; К- количество дней в году.

2. Цена покупки векселя банком или сумма, выдаваемая предъявителю учитываемого денежного обязательства по простой учетной ставке, рассчитывается по формуле:

, где

F-номинальная сумма данного обязательства;

Р- цена покупки векселя банком или это деньги, которые получает владелец векселя, в случае операции дисконтирования;

D_d-дисконт, сумма процентных денег;

(1-nd) – коэффициент дисконтирования по простой учетной ставке.

3. Процентный доход покупателя (банка) векселя по простой ставке:
Для сложной учетной ставки:

4. Формула для определения стоимости капитала, учтенного за n лет при m-кратном дисконтировании в течение года, примет вид:

. С ростом числа дисконтирования в году величина учтенного капитала возрастает.

Для облегчения расчетов при удержании сложных процентов используются дисконтные множители, которые показывают, во сколько раз уменьшится сумма при удержании с нее сложных процентов по ставке d в течение n промежутков удержания: Dis(n,d)=(1-d)ⁿ.

5. Соотношение между простыми годовыми процентными ставками r и d, обеспечивающими через период времени n получение одной и той же наращенной величины F из начального капитала Р: d(1+nr)=r.

Ставки d и r, связанные между собой этим соотношением называются эквивалентными, так как они приводят к одинаковому финансовому результату.

Пример. 3. Найти учетную ставку, эквивалентную простой процентной ставке 19%, при наращении капитала за год.

Решение. N=1, r =0,19, d=0,19/(1+0,19)»0,15966, d»16%. Т. о., учет за год по учетной ставке 16% приносит такой же доход, как наращение простыми процентами по ставке 19%.

Если время измеряется в днях t, n=t/T, где Т – временная база, равная количеству дней в году. В этом случае

Пример 4. Банк учитывает вексель за 210 дней до срока по учетной ставке 12%, используя временную базу в 360 дней. Определить доходность такой операции по процентной ставке при временной базе, равной 365.

Решение. Если разные временные базы, то получим равенство: . Отсюда следует, что

Тогда .

нахождения сложной годовой учетной ставки.

Пример 5. Вексель был учтен за полтора года до срока, при этом владелец векселя получил 0,8 от написанной на векселе суммы. По какой сложной годовой учетной ставке был учтен этот вексель?

Решение. P=0,8; n=1,5; при m=1 d=1-0,8^1/1,5=0,1382, т.е. d=13,82%

Пример 6. Векселедержатель предъявил для учета вексель на сумму 50 т.р. со сроком погашения 28.09.1997 г. Вексель предъявлен 13.09.1997 г. Банк согласился учесть вексель по учетной ставке 30% годовых. Определить сумму, которую получит векселедержатель.

Решение. P=f*(1-nd)=50*(1-15/360*0,3)=49,375 т.р.

Непрерывное наращение и дисконтирование.Уменьшая частоту начисления в пределе можно перейти к непрерывным процентам. Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала.

где е примерно равно 2,718281 –число Эйлера и r^(¥)=d -обозначение непрерывной ставки и называют ее силой роста. Сила роста характеризует интенсивность наращения за год при непрерывном начислении процентов.

Аналогично другим множителям наращения е^{d n} равен индексу роста суммы Р за n лет.

Пример. Рассчитать накопленную сумму для различных вариантов начисления процентов за один год, если исходная сумма Р=1000 руб. и номинальная годовая процентная ставка r=10%.

Непрерывное начисление процентов используется при анализе сложных финансовых задач (при выборе и обосновании инвестиционных решений). Также бывает целесообразно предполагать при оценке работы учреждения за период, в котором платежи поступают многократно, что накапливаемые суммы непрерывно меняются во времени, и применять непрерывное начисление процентов.

Бывают ситуации, когда непрерывное начисление процентов применяется непосредственно и при работе с клиентами.

Пример. На вклад в 2 тыс. руб. начисляются непрерывные проценты. Найти наращенную сумму за 7 лет, если сила роста изменяется следующим образом: в первые 2 года равна 8%, в следующие три года 10% и в каждый оставшийся год увеличивается на о,5%.

Решение.

Кредитные операции также связаны с дисконтированием. Рассмотрим операцию удержания процентов с суммы, взятой заемщиком в кредит. Проценты начисляются в начале интервала начисления и заемщик получает сумму Р за вычетом процентных денег D из суммы кредита S, которую следует вернуть. Удержание процентов можно проводить по простым и сложным процентам:

1. , где d – простая учетная ставка;

2. , где d_с- сложная учетная ставка;

3. Срок, на который выдан кредит, рассчитывается по формуле: ,

4. Учетная ставка рассчитывается по формуле:

5. При непрерывном исчислении процентов, т.е. при мультиплицирующий множитель М(m, r/m) имеет предел, равный е^r, где е-основание натуральных логарифмов (е=2,71). Непрерывным наращением процентов по ставке r называется увеличение суммы в е^r раз за единичный промежуток начисления. Непрерывным дисконтированиемназывается обратная операция непрерывному наращению, т.е. уменьшение суммы в еⁱ раз за единичный промежуток. Также справедливо следующее соотношение: .

Пример.На сумму в 2 тыс. руб. начисляются непрерывные проценты по ставке 8%. Определить наращенную сумму за 5 лет.