Наращение и дисконтирование по простым процентным ставкам

Под процентами понимают абсолютную величину дохода от предоставления денег в долг в любой форме.
При заключении финансового или кредитного соглашения стороны договариваются о размере процентной ставки- это отношение дохода к сумме долга, т.е. относительная величина дохода за фиксированный отрезок времени. Ставка измеряется в процентах в виде десятичной или обыкновенной дроби с точностью до 1/16 или 1/32.
Интервал времени, к которому относиться процентная ставка называется периодом начисления. Проценты либо выплачиваются кредитору по мере их начисления, либо присоединяются к сумме долга.
Процесс увеличения долга в связи с присоединение к сумме долга называется наращением или ростом первоначальной суммы.
Сущность метода начисления по простым процентам- проценты начисляются в течение всего срока кредита на одну и ту же величину капитала, предоставленного в кредит.
Метод начисления по сложным процентам состоит в том, что в первом периоде начисления производятся на исходную сумму кредита, затем она суммируется с начисленными процентами и проценты начисляются на наращенную сумму (проценты на проценты).
Процентные ставки могут быть: постоянными (фиксированными) и переменными (плавающими). Во втором случае указывается изменяющейся во времени базовая ставка (база) и размер надбавки к ней (маржа). Размер маржи часто определяется сроком операции и финансовым положением заемщика, как правило, изменяется от 0,5% до 5%.

При последовательном погашении задолженности возможны 2 способа начисления процентов:

1. процентная ставка (как простая, так и сложная) применяется к фактической сумме долга.

2. простые проценты начисляются сразу на всю сумму долга без учета последовательного его погашения.

В практических расчетах применяется так называемые дискретные - начисления за фиксированные интервала времени. В некоторых случаях (аналитических финансовых расчетах) используют непрерывные проценты, когда наращение производится за бесконечно малые промежутки времени.

Однако как бы ни отличались ставки процента, все они находятся под воздействием рыночного механизма: если предложение денег уменьшается, то процентные ставки увеличиваются, и наоборот. Именно поэтому рассмотрение всех процентных ставок можно свести к изучению закономерностей одной процентной ставки и в дальнейшем оперировать термином "процентная ставка"

Под наращенной суммой ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока.

,

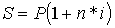
где P - первоначальная сумма,

n - срок,

i - ставка наращения (десятичная дробь).

В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. При этом наращенная на конец срока сумма определяется по следующему уравнению:

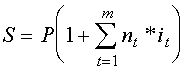
где 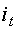- ставка простых процентов в периоде t, t=1,2,...,m;

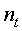- продолжительность периода ; .

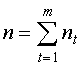В практике при инвестировании средств в краткосрочные депозиты прибегают к последовательному неоднократному повторению наращения по простым процентам в пределах заданного общего срока т.е. реинвестированию полученных на каждом этапе наращения средств. В этом случае :

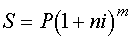, (3.3)

где m - количество реинвестиций.

Термин дисконтирование употребляется как средство определения

любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени.

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n , необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты - дисконтом. В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором - учетная ставка.

Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды.

,

,

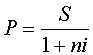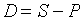где D - дисконта.

Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. При учете векселя применяется банковский или коммерческий учет, согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.

,

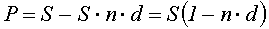Для ставки наращения прямой задачей является определение наращенной суммы, обратной - дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная - в наращении.

Ставка Прямая задача Обратная задача

i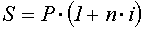

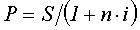
d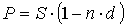

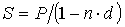
Учетная ставка отражает фактор времени более жестко. Например, при d = 20 % уже 5-ти летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете.