Различное положение плоскости относительно

Плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный aП1; - фронтальный aП2; - профильный aП3).

Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.42).

2.Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2.1. Плоскость перпендикулярная горизонтальной плоскости проекций (a^P1), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.43).

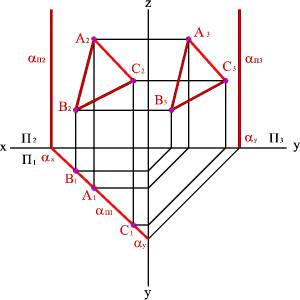
Рис. 43. Горизонтально проецирующая плоскость

2.2. Плоскость перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом aП2 (рис.44).

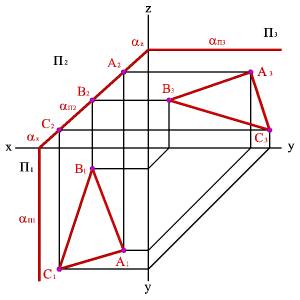
Рисунок 44. Фронтально проецирующая плоскость

2.3. Плоскость перпендикулярная профильной плоскости (a^П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.45).

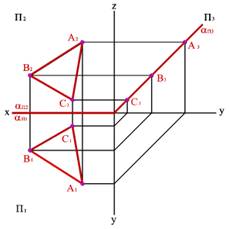Рисунок 45. Биссекторная плоскость

3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:

3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (a//П1) - (a^П2,a^П3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости aП2 и aП3 (рис.46).

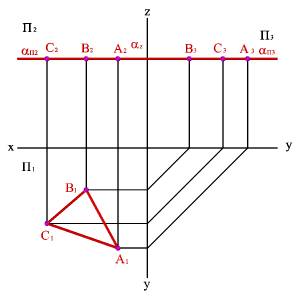
Рисунок 46. Горизонтальная плоскость

3.2. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (a//П2), (a^П1, a^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые - следы плоскости aП1 и aП3 (рис.47).

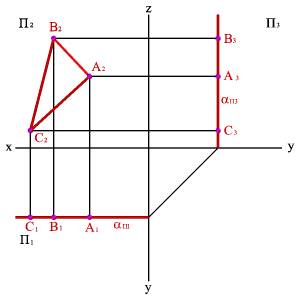
Рисунок 47. Фронтальная плоскость

3.3. Профильная плоскость - плоскость параллельная профильной плоскости проекций (a//П3), (a^П1, a^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости aП1 и aП2 (рис.48).

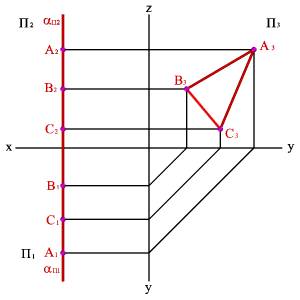
Рисунок 48. Профильная плоскость

Следы плоскости

Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.

Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой ( как для построения любой прямой). На рис. 49 показано нахождение следов плоскости α(АВС). Фронтальный след плоскости αП2, построен, как прямая соединяющая две точки N(АС) и N(АВ), являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный след αП1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след αП3 – прямая соединяющая точки (αy и αz) пересечения горизонтального и фронтального следов с осями.

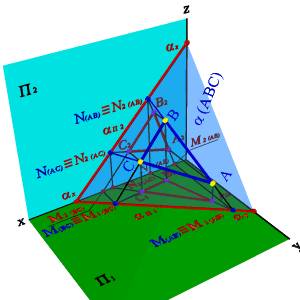
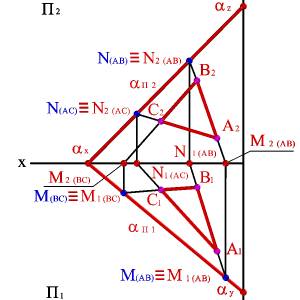
Рис. 49. Построение следов плоскости