Количественные показатели оценки риска.

На этапе количественного анализа риска вычисляются числовые значения величин отдельных рисков и риска объекта в целом. Также выявляется возможный ущерб и дается стоимостная оценка от проявления риска и, наконец, завершающей стадией количественной оценки является выработка системы антирисковых мероприятий и расчет их стоимостного эквивалента. Количественный анализ можно формализовать, для чего используется инструментарий теории вероятностей, математической статистики, теории исследования операций. Наиболее распространенными методами количественного анализа риска являются статистические, аналитические, метод экспертных оценок, метод аналогов.

Статистические методы.

Суть статистических методов оценки риска заключается в определении вероятности возникновения потерь на основе статистических данных предшествующего периода и установлении области (зоны) риска, коэффициента риска и т.д. Достоинствами статистических методов является возможность анализировать и оценивать различные варианты развития событий и учитывать разные факторы рисков в рамках одного подхода. Основным недостатком этих методов считается необходимость использования в них вероятностных характеристик. Возможно применение следующих статистических методов: оценка вероятности исполнения, анализ вероятного распределения потока платежей, деревья решений, имитационное моделирование рисков, коэффициент бета.

Величина риска (степень риска) измеряется двумя критериями:

1) среднее ожидаемое значение;

2) колеблемость (изменчивость) возможного результата.

Среднее ожидаемое значение — это то значение величины события, которое связано с неопределенной ситуацией. Среднее ожидаемое значение является средневзвешенным для всех возможных результатов, где вероятность каждого результата используется в качестве частоты или веса соответствующего значения. Среднее ожидаемое значение измеряет результат, который мы ожидаем в среднем.

Т. Е. если известно, что при вложении капитала в мероприятие А из 120 случаев прибыль 250 тыс. руб. была получена в 48 случаях (вероятность 0,4), прибыль 200 тыс. руб. была получена в 36 случаях (вероятность 0,3) и прибыль 300 тыс. руб. была получена в 36 случаях (вероятность 0,3), то среднее ожидаемое значение составит (250 х 0,4 + 200 х 0,3 + 300 х 0,3) = 250 тыс. руб.

Аналогично находим, что при вложении капитала в мероприятие Б средняя прибыль составила (400x0,3 + 300x0,5 + + 150 х 0,2) = 300 тыс. руб.

Среднее ожидаемое значение определяется по формуле:

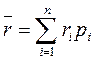
r – произвольное мероприятие, которое может иметь n возможных исходов r_i, а каждый исход имеет вероятность p_i.

Средняя величина представляет собой обобщенную количественную характеристику и не позволяет принять решения в пользу какого-либо варианта вложения капитала.

Для окончательного принятия решения необходимо измерить колеблемость показателей, т. е. определить меру колеблемости возможного результата.

Колеблемость возможного результата представляет собой степень отклонения ожидаемого значения от средней величины.

Для этого на практике обычно применяются два близко связанных критерия: дисперсия и среднее квадратическое отклонение.

Дисперсия представляет собой средневзвешенное из квадратов отклонений действительных результатов от средних ожидаемых.

;

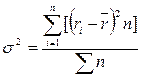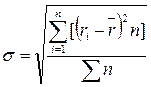
где σ² —дисперсия;

σ – среднее квадратичное отклонение

r_i – ожидаемое значение для каждого случая наблюдения;

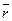– среднее ожидаемое значение;

п – число случаев наблюдения (частота).

Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости.

Ковариация – показатель сближения любой пары произвольных переменных. Например, при неожиданном росте процентных ставок фондовый индекс имеет тенденцию к понижению. Это пример двух переменных с отрицательной ковариацией.

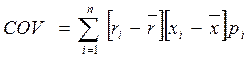
r и х – случайные величины

n – количество возможных общих исходов для r и х

p_i – вероятность наступления i-того исхода.

Недостатки показателя ковариации:

1. ковариация не имеет пределов и может оказаться любым числом, большим или малым.

2. числовое значение ковариации зависит от единиц измерения, применяемых в отношении случайных величин. Например, числовое значение ковариации между ростом и весом человека зависит от того, измеряются ли эти величины в дюймах и футах, или сантиметрах и килограммах. Поэтому трудно проводить сравнение различных значений ковариации.

Задачу сравнения степени связи между различными парами случайных величин можно более эффективно решить при помощи коэффициента корреляции, который колеблется в диапазоне от -1 до +1.

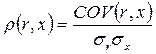
Для анализа риска обычно используют коэффициент вариации. Он представляет собой отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений.

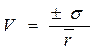
где V —коэффициент вариации, %;

Вариация – это особый случай ковариации актива с самим собой.

Коэффициент вариации — относительная величина. Поэтому на размер этого коэффициента не оказывают влияние абсолютные значения изучаемого показателя. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации стандартизирует среднее квадратическое отклонение и позволяет рассчитать риск, приходящийся на единицу доходности.

Коэффициент вариации может изменяться от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации: до 10% — слабая колеблемость; 10-25% — умеренная колеблемость; свыше 25% — высокая колеблемость.

«Дерево» вероятностей.

Финансовый риск представляет собой функцию времени. Как правило, степень риска для данного финансового актива или варианта вложения капитала увеличивается во времени. Например, убытки импортера сегодня зависят от времени от момента заключения контракта до срока платежа по сделке, так как курсы иностранной валюты по отношению к российскому рублю продолжают расти.

Метод дерева вероятностей распространен в зарубежной практике. Он позволяет точно определить вероятные будущие денежные потоки инвестиционного проекта в их связи с результатами предыдущих периодов времени. Если проект вложения капитала приемлем в первом периоде времени, то он может быть также приемлем и в последующих периодах времени.

Если же предполагается, что денежные потоки в разных периодах времени являются независимыми друг от друга, тогда необходимо определить вероятное распределение результатов денежных потоков для каждого периода времени.

В случае, когда связь между денежными потоками в разных периодах времени существует, необходимо принять данную зависимость и на ее основе представить будущие события так, как они могут произойти.

В качестве примера произведем дерево вероятностей для трех периодов времени (рис.).

Дерево вероятностей показывает, что если в периоде 1 результатом будет верхняя ветвь, то она приведет в периоде 2 к другому множеству возможных результатов, чем это было бы, если бы результат в периоде 1 выражался нижней ветвью. Аналогичная картина наблюдается и при переходе от периода времени 2 к периоду 3. Для каждой из ветвей денежные потоки привязаны к вероятности.

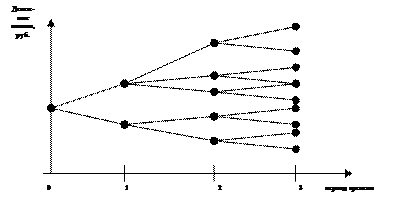
В периоде 1 результат денежного потока не зависит от того, что было прежде. Поэтому вероятности, связанные с двумя ветвями, называются исходными вероятностями. Для всех последующих периодов (т. е. периодов 2, 3 и т. Д.) результаты денежных потоков зависят от предыдущих результатов. Поэтому вероятности этих периодов называются условными. Кроме того, существует совместная вероятность, которая представляет собой вероятность по­явления определенной последовательности денежных потоков. Совместная вероятность равна произведению исходной и услов­ной вероятностей.

Рассмотрим пример.

Фирма оценивает возможность производства нового товара А со сроком использования два года. Стоимость товара 1000 тыс. руб. Величина денежного потока зависит от спроса на данный товар. Дерево вероятностей возможных будущих денежных потоков, связанных с новым товаром, имеет вид (см. табл.):

Таблица. Иллюстрация дерева вероятностей денежных потоков при производстве и реализации нового товара А

1-й год	2-й год	Ветвь
Исходная вероятность	Денежный поток (прогноз), тыс. руб.	Условная вероятность	Денежный поток (прогноз), тыс. руб.	№ ветви	Совместная вероятность
0,4	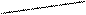300	0,3			0,4*0,3 = 0,12
0,7			0,4*0,7 = 0,28
0,6	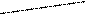600	0,4			0,6*0,4 = 0,24
0,6			0,6*0,6 = 0,36
	Итого: 1,0

Таким образом, риск имеет математически выраженную вероятность наступления потери, которая опирается на статистические данные и может быть рассчитана с достаточно высокой степенью точности. Для количественной оценки риска необходимо знать все возможные последствия отдельного действия и вероятность их возникновения.

Аналитические методы.

Позволяют определить вероятность возникновения потерь на основе математических моделей и используются в основном для анализа риска инвестиционных проектов. Возможно использование таких методов, как анализ чувствительности, метод корректировки нормы дисконта с учетом риска, метод эквивалентов, метод сценариев.

Анализ чувствительности сводится к исследованию зависимости некоторого результирующего показателя от вариации значений показателей, участвующих в его определении. Другими словами, этот метод позволяет получить ответы на вопросы вида: что будет с результирующей величиной, если изменится значение некоторой исходной величины?

Метод корректировки нормы дисконта с учетом риска является наиболее простым и вследствие этого наиболее применяемым на практике. Основная его идея заключается в корректировке некоторой базовой нормы дисконта, которая считается безрисковой или минимально приемлемой. Корректировка осуществляется путем прибавления величины требуемой премии за риск.

С помощью метода достоверных эквивалентов осуществляется корректировка ожидаемых значений потока платежей путем введения специальных понижающих коэффициентов с целью приведения ожидаемых поступлений к величинам платежей, получение которых практически не вызывает сомнений и значения которых могут быть достоверно определены.

Метод сценариев позволяет совместить исследование чувствительности результирующего показателя с анализом вероятностных оценок его отклонений. С помощью этого метода можно получить достаточно наглядную картину для различных вариантов событий. Он представляет собой развитие методики анализа чувствительности, так как включает одновременное изменение нескольких факторов.

Метод экспертных оценок (см. п. 3.1).