Взаимоисключающие инвестиции
Если осуществление любого инвестиционного проекта из некоторого набора уменьшит доходность остальных инвестиций, они называются взаимозаменяемыми. Крайний случай взаимозаменяемости возникает, когда осуществление одного из инвестиционных проектов делает невозможным получение денежных доходов от остальных инвестиций. Такие инвестиции называются взаимоисключающими.
Такой тип инвестиций очень распространен в промышленности, и методы IRR и NPV очень часто по-разному ранжируют один и тот же набор взаимоисключающих инвестиций.
Таблица 3.4
Взаимоисключающие проекты
| Проект | Величина инвестиций | NPV | IRR |
| А | - 700 000 | 40 000 | |
| Б | -100 000 | 20 000 |
Если проекты А и Б рассматриваются изолированно, то каждый из них должен быть одобрен, поскольку они удовлетворяют всем критериям. Однако если проекты являются альтернативными, то выбор не очевиден, так как проект А имеет выше значение NPV, зато проект Б предпочтительнее по показателю IRR.
При принятии решения можно руководствоваться следующими соображениями:
а) рекомендуется выбирать вариант с большим NPV, поскольку этот показатель характеризует возможный прирост экономического потенциала предприятия (наращивание экономической мощи предприятия является одной из наиболее приоритетных целевых установок);
б) необходимо учесть эффект масштаба (о нем речь пойдет ниже).
Исследования, проведенные крупнейшими специалистами в области финансового анализа, показали, что наиболее предпочтительным критерием является критерий NPV. Основных аргументов в пользу этого критерия два:
1) он дает вероятную оценку прироста капитала предприятия в случае принятия проекта; критерий в полной мере отвечает основной цели деятельности управленческого персонала, которой является наращивание экономического потенциала предприятия;
2) он обладает свойством аддитивности, что позволяет складывать значения показателя NPV по различным проектам и использовать агрегированную величину для оптимизации инвестиционного портфеля.
Что касается показателяIRR, то он имеет ряд серьезных недостатков. Коротко охарактеризуем их.
1. В сравнительном анализе альтернативных проектов критерий IRR можно использовать достаточно условно. Так, если расчет критерия IRR для двух проектов показал, что его значение для проекта А больше, чем для проекта Б, то в определенном смысле проект А может рассматриваться как более предпочтительный, поскольку допускает большую гибкость в варьировании источниками финансирования инвестиций, цена которых может существенно различаться. Однако такое предпочтение носит весьма условный характер.
Поскольку IRR является относительным показателем, на его основе невозможно сделать правильные выводы об альтернативных проектах с цозиции их возможного вклада в увеличение капитала предприятия; этот недостаток особенно сильно проявляется, если проекты существенно различаются по величине денежных потоков.
Таблица 3.5
Сравнительный анализ проектов
| Проект | Величина инвестиций | NPV | IRR |
| А | - 1 000 | 3 000 | |
| Б | -100 000 | 20 000 |
Например, проект А может казаться более предпочтительным, поскольку его IRR значительно превосходит IRR второго проекта. Однако если предприятие имеет возможность профинансировать проект Б, его, безусловно, следует предпочесть, поскольку вклад этого проекта в увеличение капитала компании на порядок превосходит вклад проекта А.
2. Критерий IRR показывает лишь максимальный уровень затрат, который может быть ассоциирован с оцениваемым проектом. В частности, если цена инвестиций в оба альтернативных проекта меньше, чем значения IRR, для них выбор может быть сделан, лишь с помощью дополнительных критериев. Более того, критерий IRR не позволяет различать ситуации, когда цена капитала меняется. Рассмотрим соответствующий пример. Расстроим графики функции NPV=f(r) для гипотетических проектов А и Б.
NPV
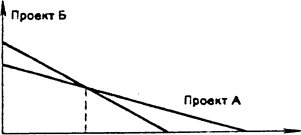
Точка Фишера r
Рис. 3.1. Точка Фишера.
Точка пересечения двух графиков, показывающая значение коэффициента дисконтирования, при котором оба проекта имеют одинаковый NPV, называется точкой Фишера. Она примечательна тем, что служит пограничной точкой, разделяющей ситуации, которые улавливаются критерием NPV и не улавливаются критерием IRR.
Иногда критерий IRR не только не может расставить приоритеты между проектами, но и не показывает различия между ситуациями, когда ставка дисконтирования больше или меньше ставки точки Фишера. Напротив, критерий NPV позволяет расставить приоритеты в любой ситуации. Если ставка дисконтирования меньше точки Фишера, то следует предпочесть проект Б, и наоборот.
То же самое демонстрирует эффект масштаба.
Цель – показать, что при анализе взаимоисключающих инвестиций результаты ранжирования по IRR менее надежны, чем по NPV.
Пример (ставка дисконтирования 10%).
Таблица 3.6
Сравнительный анализ проектов
| Проект | Денежные потоки | IRR | |
| 1 год | 2 год | ||
| А | - 10 000 | 12 000 | |
| Б | -15 000 | 17 700 | |
| Б-А | - 5 000 | 5 700 |
Исходя из критерия IRR, проект А более желателен.
Учитывая же эффект масштаба, замечаем, что проект Б требует дополнительных вложений 5 000 и дает отдачу в 5 700. Внутренняя норма окупаемости дополнительных денежных потоков равна 14 % (5700/5000=1,14 и это соответствует точке Фишера). Это – инвестиционная возможность компании, если она сможет привлечь дополнительные средства по 10 %. Вложив капитал в проект А, мы сэкономим 5 000, которые принесут 5 500 при доходности 10% годовых (5000*1,1=5500). Это меньше, чем 5 700, которые можно получить, инвестировав дополнительные средства в проект Б.
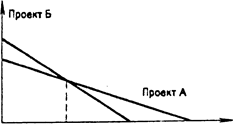
Рис. 3.2. Точка Фишера.
Как видно из рисунка 3.2, инвестиционный проект Б более желателен при ставке дисконтирования меньше 14%.
Таким образом, при анализе инвестиций методом IRR нельзя упускать из виду размер инвестиций.
Если взаимоисключающих инвестиций больше двух, то придется попарно сравнивать инвестиционные проекты и, повторив процедуру n-1 раз, получим проект-победитель.
3. Одним из существенных недостатков критерия IRR является и то, что в отличие от критерия NPV он не обладает свойством аддитивности, т. е. для двух инвестиционных проектов А и Б, которые могут быть осуществлены одновременно:
IRR (А+Б)¹IRR(А)+IRR(Б).
NPV обладает этим свойством.
4. Критерий IRR. совершенно не пригоден для анализа неординарных инвестиционных потоков (название условное). В предыдущих параграфах рассматривались стандартные, наиболее простые и типичные ситуации, когда денежный поток развивается по вполне определенной схеме: инвестиция или отток капитала (со знаком “—” в расчетах) и поступления или приток капитала (со знаком “+” в расчетах). Однако возможны и другие, неординарные, ситуации, когда отток и приток капитала чередуются. В частности, вполне реальна ситуация, когда проект завершается оттоком капитала.
Для ранжирования взаимоисключающих проектов NPV может служить критерием тогда, когда ставка дисконтирования равняется соответствующей альтернативной стоимости капитала.
IRR предпочтительно использовать для того, чтобы знать разницу между прогнозируемой IRR и требуемой доходностью. Эта разница — запас прочности, позволяющей сопоставить доходность инвестиций и риск.
Если применяется метод NPV, то правила принятия инвестиционных решений следующие:
1. Для каждого проекта рассчитать NPV, используя в качестве ставки дисконтирования стоимость капитала.
2. Если необходимо принять решение о том, одобрить инвестиционный проект или нет, то критерий NPV>0.
3. Если есть набор взаимоисключающих инвестиций, но осуществить можно только один, то надо взять проект с максимальной NPV.
Метод IRR тоже можно использовать для выбора между несколькими инвестиционными проектами, если стоимость денег во все будущие периоды времени одна и та же. Если метод используется правильно, то он приведет к тому же решению, что и метод NPV. Но правила использования IRR сложнее:
1. Один и тот же проект может иметь несколько IRR.
2. Находить наилучший проект из взаимоисключающих попарным методом — трудоемкая задача.
3. Анализируя IRR проекта, необходимо определить, соответствуют ли денежные потоки обычному традиционному проекту: у денежных потоков заемного типа (когда за положительными денежными потоками идут отрицательные) кривая NPV имеет положительный наклон и NPV растет с ростом ставки дисконтирования.
4. Если стоимость капитала во времени меняется, лучше применять метод NPV.
