Учет инфляции в финансово-экономических расчетах
Базовыми понятиями, связанными с помещением капитала в условиях инфляции, являются следующие.
Индекс роста цен рассчитывается следующим образом:
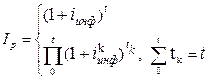(13)
где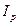 
- индекс роста цен;
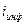- годовой темп инфляции, носящий равномерный характер в пределах всего срока помещения капитала;
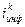- годовой темп инфляции, носящий неравномерный характер в пределах всего срока помещения капитала;
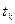- продолжительность периода времени, в котором инфляция составляет , %;
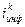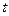- срок помещения капитала.
Индекс покупательной способности денег рассчитывается по формуле (14):
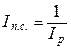, (14)
где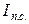 
- индекс покупательной способности денег.
Номинальная процентная ставка (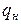 
) – годовая процентная ставка, работающая в условиях инфляции. Она отражает норму годового прироста капитала по номиналу.
Реальная процентная ставка (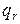 
) – годовая процентная ставка, отражающая рост капитала в условиях инфляции с учетом покупательной способности денег.
Взаимосвязь номинальной и реальной процентных ставок:
- для простых процентов:
а) если известна реальная норма доходности в заданных условиях инфляции, но номинальная процентная ставка рассчитывается по формуле (15):
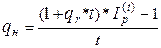, (15)
б) если известна номинальная процентная ставка и условия инфляции, то реальная процентная ставка рассчитывается по формуле (16):
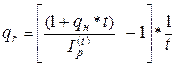, (16)
где 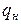- годовая номинальная процентная ставка (ставка-брутто);
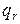- годовая реальная процентная ставка (ставка-нетто);
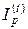- индекс роста цен за весь срок помещения капитала;
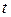- срок помещения капитала;
- для сложных процентов (при постоянной процентной ставке и уровне инфляции):
а) если известна реальная процентная ставка и условия инфляции (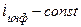 
), то номинальная процентная ставка рассчитывается по формуле (17):
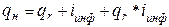, (17)
а) если известна номинальньная процентная ставка и условия инфляции, то реальная процентная ставка рассчитывается по формуле 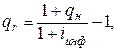(18):
(18)
где 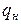- годовая номинальная процентная ставка (ставка-брутто);
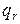- годовая реальная процентная ставка (ставка-нетто);
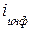- годовой индекс инфляции.
При отрицательном уровне реальной процентной ставки происходит эрозия капитала.
Барьерная процентная ставка (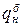 
) – это такая годовая номинальная процентная ставка, которая обеспечивает только погашение инфляционных потерь. Барьерная процентная ставка определяется из условия равенства множителя наращения капитала и индекса роста цен ( 
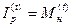) и определяется следующим образом:
- для простых процентов:
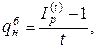(19)
- для сложных процентов (эффективной процентной ставки):
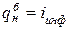, (20)
- для сложных процентов (номинальной процентной ставки):
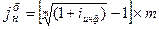, (21)
где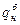 
- барьерная процентная ставка, которая обеспечивает погашение только инфляционных потерь, при этом покупательная способность наращенной стоимости равна стартовой сумме капитала;
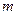- периодичность начисления процентов в течение года.
Исходные данные для решения задач
Варианты 0-4. 1. Рассчитать наращенную стоимость капитала при начислении: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением в течение года).
2. Определить реальную доходность от начисления: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением).
Исходные данные для расчетов представлены в таблице 1.
Таблица 1 – Исходные данные для расчетов
| Показатели | Варианты | ||||||||
| 1. Стартовая сумма капитала, тыс.руб. | ? | ? | ? | ? | |||||
| 2. Наращенная стои-мость капитала, тыс.руб. | ? | ? | ? | ? | ? | ||||
| 3. Срок помещения капитала, лет | |||||||||
| 4. Процентная ставка, % годовых | 12,5 | ? | ? | ? | ? |
Продолжение таблицы 1
| 5.Периодичность начис-ления процентов в течение года, раз | |||||||||
| 6. Годовой уровень инфляции, % | 7,5 | 8,6 | 8,4 | 7,8 | 8,6 | 7,9 | 8,2 | 8,0 | |
| 7. Реальный уровень дохода, % годовых | ? | ? | ? | ? | ? | 2,5 | 1,5 |
Варианты 5-8. 1. Рассчитать размер процентной ставки, под которую необходимо поместить капитал в заданных условиях инфляции при начислении: а) простых процентов; б) сложных процентов (с их разовым начислением в течение года).
2. Рассчитать стартовую сумму капитала при начислении: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением).
Варианты 0-8. 1. Рассчитать срок, необходимый для увеличения стартовой суммы капитала в четыре раза при начислении: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением).
2. Рассчитать наращенную стоимость капитала в условиях инфляции, если процентная ставка ежегодно увеличивается на 1% при начислении: а) простых процентов; б) сложных процентов.
По результатам всех расчетов сделать выводы.
Варианты 9-14. 1. Рассчитать размер годовой процентной ставки, под которую необходимо поместить капитал в заданных условиях инфляции при начислении: а) простых процентов; б) сложных процентов (с их разовым начислением в течение года).
2. Определить реальную доходность от начисления: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением в течение года).
3. Рассчитать срок, необходимый для увеличения стартовой суммы капитала по номиналу в 4 раза при начислении: а) простых процентов; б) сложных процентов (исходя их рассчитанной процентной ставки при однократном и многоратном начислении процентов в течение года).
Исходные данные для расчетов представлены в таблице 2.
Варианты 15-19. 1. Рассчитать срок наращения капитала при начислении: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением).
2. Определить реальную доходность (в виде годовой процентной ставки) от начисления: а) простых процентов; б) сложных процентов.
3. Какая номинальная процентная ставка эквивалентна заданной эффективной (стр. 3, табл. 2) при заданной частоте начисления процентов (стр. 4, табл. 2).
4. Рассчитать эквивалентную ей простую процентную ставку.
Таблица 2 – Исходные данные для расчетов 
| Показатели | Варианты | ||||||||||
| 1. Стартовая сумма капитала, тыс.руб. | |||||||||||
| 2. Наращенная стоимость капи-тала, тыс.руб. | |||||||||||
| 3. Срок помеще-ния капитала, лет | ? | ? | ? | ? | ? | ||||||
| 4. Процентная ставка,% годовых | ? | ? | ? | ? | ? | ? | |||||
| 5. Периодичность начисления про-центов в течение года, раз | |||||||||||
| 6. Годовой уровень инфляции, % | 7,9 | 8,2 | 8,8 | 8,6 | 6,9 | 7,4 | 8,0 | 8,7 | 9,0 | 8,5 | 9,2 |
| 7. Реальный уровень дохода, % годовых | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Варианты 9-19. Рассчитать размер барьерной процентной ставки при начислении: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением в течение года).
Варианты 20-24.1. Рассчитать множитель наращения капитала при начислении: а) простых процентов; б) сложных процентов (с их начисление в конце каждого года и многократно).
2. Рассчитать реальную норму доходности при начислении: а) простых процентов; б) сложных процентов (с их начисление в конце каждого года и многократно).
3. Если заданная процентная ставка является простой (таблица 3, стр. 4), то чему будет равна эквивалентная ей сложная процентная ставка (при их начислении в конце каждого года и с заданной периодичностью)?
4. Рассчитать наращенную стоимость капитала при начислении сложных процентов (стр. 4, таблица 3) с заданной частотой их начисления (стр. 6, табл. 3) при условии, что через три года заданная процентная ставка увеличится на, % (стр. 5, табл. 3).
Исходная информация для расчетов представлена в таблице 3.
Таблица 3 – Исходные данные для расчетов
| Показатели | Варианты | |||||||||
| 1. Стартовая сумма капитала, тыс.руб. | ||||||||||
| 2. Множитель наращения капитала | ? | ? | ? | ? | ? | 4,5 | 2,2 | 3,6 | 4,8 | |
| 3. Срок помещения капитала, лет | 7,5 | 6,5 | ? | ? | ? | ? | ? | |||
| 4. Процентная ставка, % годовых | 11,6 | 12,1 | 11,4 | 10,5 | 13,5 | 12,5 | 13,2 | |||
| 5. Увеличение процент-ной ставки на, % | 2,5 | 1,8 | 2,4 | 3,6 | ||||||
| 6. Периодичность начисления процентов в течение года, раз | ||||||||||
| 7. Квартальный уровень инфляции, % | 2,45 | 2,29 | 1,85 | 1,99 | 2,2 | - | - | - | - | - |
| 8. Полугодовой уровень инфляции, % | 3,8 | 3,2 | 5,1 | 4,4 |
Варианты 25-29. 1. Рассчитать срок помещения капитала при начислении: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением).
2. Определить величину реальной нормы доходности при начислении процентов по заданной норме доходности (стр. 4, таблица 3): а) простых процентов; б) сложных процентов (с их разовым и многократным начислением).
3. Рассчитать размер барьерной процентной ставки для условий начисления: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением).
4. Рассчитать наращенную стоимость капитала при начислении: а) простых процентов; б) сложных процентов (с их разовым и многократным начислением) для условий увеличения процентной ставки в размере (таблица 3, стр. 5).
Выполнить сравнительный анализ результатов расчетов.
Оценка денежных потоков
Одним из основных элементов финансово-экономического анализа является оценка денежного потока, генерируемого в течение ряда временных интервалов в результате реализации какого-либо проекта или функционирования того или иного вида активов.
Оценка денежного потока осуществляется как с позиций настоящего, так и с позиций будущего момента времени.