Сновные понятия системного анализа

Общее число понятий, специфических для системных исследований, чрезвычайно велико. Поэтому ограничимся лишь наиболее важными из них.

Система. Термин “система” используется в тех случаях, когда хотят охарактеризовать исследуемый или проектируемый объект как нечто целое (единое), сложное, о котором невозможно сразу дать представление, показав его, изобразив графически или описав математическим выражением.

Система (греч. – “составленное из частей”, “соединение”) – объективное единство закономерно связанных друг с другом предметов, явлений, а также знаний о природе и обществе (БСЭ, Т. 39, с. 158).

Как и всякое фундаментальное понятие, этот термин лучше всего определяется в процессе рассмотрения его основных свойств. Таких свойств можно выделить четыре.

1. Система есть прежде всего совокупность элементов. При определенных условиях элементы могут рассматриваться как системы.

2. Наличие существенных связей между элементами и (или) их свойствами, превосходящие по силе (мощности) связи этих элементов с элементами, не входящими в данную систему. Под существенными связями понимаются такие, которые закономерно, с необходимостью определяют интегративные свойства системы.

3. Наличие определенной организации, что проявляется в снижении неопределенности системы.

4. Существование интегративных свойств, т.е. присущих системе в целом, но не свойственных ни одному из ее элементов в отдельности. А это значит, что система не сводится к простой совокупности элементов, и проводя декомпозицию системы, нельзя познать все свойства системы в целом.

Таким образом, в самом общем случае понятие “система” характеризуется: наличием множества элементов; наличием связей между ними; целостным характером данного множества элементов или просессов.

Обобщая различные определения системы, можно записать следующее формальное определение системы:

S = < A, R, Z, N, G >,

где A = a_i - множество элементов системы;

R = r_ij - множество связей (отношений) между элементами;

Z = z_j - множество целей системы;

N – наблюдатель (исследователь) – лицо, исследующее систему или

принимающее решение;

G – метод моделирования, с помощью которого наблюдатель описывает

систему или процесс принятия решения в ней.

Рассмотрим основные понятия, позволяющие описывать систему.

Элемент. Под элементом принято понимать простейшую неделимую часть системы. Однако ответна вопрос, что является такой частью, может быть неоднозначным.

Например, в качестве элементов стола можно назвать «ножки, ящики, крышку и т.д.», а можно — «атомы, молекулы», в зависимости от того, какая задача стоит перед исследователем. Аналогично в системе управления пред­приятием элементами можно считать приказы, распоряжения, положения и дру­гие нормативно-методические или нормативно-технические документы, регламен­тирующие процессы управления, а можно — показатели, реквизиты, отдельные операции организационно-технологических процедур подготовки н реализации управленческих решений.

Поэтому примем следующее определение: элемент— это предел членения системы, с точки зрения аспекта рассмотрения системы, решения конкретной задачи, поставленной цели.

Систему можно расчленять на элементы различными способами в зависимости от формулировки задачи, цели и ее уточнения в про­цессе системного анализа. При необходимости можно изменять принцип расчленения, выделять другие элементы системы и полу­чать с помощью этого нового расчленения более адекватное пред­ставление об анализируемом объекте или проблемной ситуации.

Иногда термин элемент используют и в более широком смысле, даже в тех случаях, когда система не может быть расчленена сразу на составляющие, являющиеся пределом ее членения. Однако при многоуровневом членении системы лучше использовать другие термины, преду­смотренные в теории систем: сложные системы принято вначале делить на подсистемы, а если последние также сразу трудно раз­делить на элементы, то составляющие промежуточных уровней (если неизвестен их характер) называют компонентами системы.

Деление на подсистемы связано с возможностью вычленения совокупностей взаимосвязанных элементов (или компонентов), способных выполнять относительно независимые функции, под­цели, направленные на достижение общей цели системы. Назва­нием подсистемаподчеркивается, что такая часть должна обла­дать свойствами системы (в частности, свойством целостности). Этим подсистема отличается от группы элементов, для которых не определена подцель и не выполняется свойство целостности. Для таких групп используется понятие компонентов.

Расчленяя систему на подсистемы, следует иметь в виду, что так же, как и при расчленении на элементы, выделение подсистем зависит от цели и поможет меняться по мере ее уточнения и раз­вития представлений исследователя об анализируемом объекте или проблемной ситуации.

Связь. Понятие связь входит в любое определение системы и обеспечивает возникновение и сохранение целостных ее свойств. Это понятие одновременно характеризует и строение (статику), и функционирование (динамику) системы.

Связь определяют как ограничение степени свободы элементов. Действительно, элементы, вступая в связь друг с другом, утрачи­вают часть своих свойств, которыми они потенциально обладали в свободном состоянии. Например, рассматривая процедуру “заем денег”, мы видим, что связь, возникающая между кредитором и заемщиком, ограничивает права (степени свободы) должника и добавляет степени свободы (права) кредитору.

Связи можно охарактеризовать (рис.2) направлением, силой, характе­ром (или видом). По первому признаку связи делят на направленныеи ненаправленные. По второму — на сильныеи слабые (иногда пытаются ввести «шкалу» силы связей для конкретной задачи). По характеру (виду) различают связи подчинения, связи порожде­ния (или генетические), равноправные (связи координации), связи управления. Некоторые из этих классов можно разделить более детально: например, связи подчинения могут быть типа «род— вид», «часть—целое», связи порождения — типа «причина—след­ствие». Связи можно разделить также по месту приложения (на внутренниеи внешние), по направленности процессов в системе в целом или в отдельных ее подсистемах (прямые и обратные)и по некоторым более частным признакам.

Связи в конкретных системах могут быть одновременно охарак­теризованы несколькими из названных признаков.

Виды связей

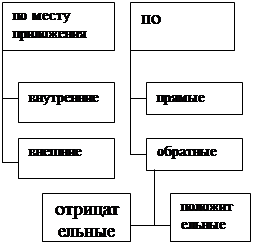Рис.2. Классификация видов связей

Очень важную роль в моделировании систем играет понятие обратной связи. Обратная связь может быть положительной,— сохраняющей тенденции происходящих в системе изменений того или иного выходного параметра, и отрицательной, — противо­действующей тенденциям изменения выходного параметра, т. е. направленной на сохранение требуемого значения этого параметра. Например. Положительная обратная связь: при низкой собираемости налогов увеличивать налоговое бремя, стимулируя дальнейшее снижение собираемости. Отрицательная обратная связь: при низкой собираемости налогов снизить налоговое бремя, создать стимулы для уплаты налогов и этим повысить их собираемость.

Понятие обратной связи, хорошо известное инженерам и обыч­но иллюстрируемое на примерах технических устройств, не всегда легко интерпретируется в конкретных условиях организационных систем управления. При практическом использовании этого поня­тия часто ограничиваются только фиксацией рассогласования меж­ду требуемым и фактическим значением регулируемого параметра, а необходимо учитывать и реализовывать все элементы цепи об­ратной связи, не забывать ее «замкнуть».

Обратная связь является основой саморегулирования, раз­вития систем, приспособления их к меняющимся условиям суще­ствования. Как правило, при разработке моделей функциониро­вания сложных саморегулирующихся, самоорганизующихся сис­тем в них одновременно присутствуют и отрицательная, и поло­жительная обратные связи.

Теоретически для того, чтобы систе­ма не распалась на части, необходимо обеспечивать превышение суммарной силы (мощности) связей между элементами системы, т. е. внутренних связей w^R_в, над суммарной мощностью связей между элементами системы и элементами среды, т. е. внешних связей w^R_ср

w^R_ср < w^R_в

Однако на практике в организационныхсистемах подобные измерения трудно реализовать. Можно ввести лишь некоторые косвенные оценки, характеризующие выполнение необходимых требований.

А можно ли связь выразить количественно? Количество связей, определяемое числом возможных сочетаний между элементами, может быть найдено по формуле

C = n (n – 1),

где n – количество элементов, входящих в систему.

Цель. Понятие цель и связанные с ним понятия целесообраз­ности, целенаправленности лежат в основе развития системы.

Анализ определений цели и связанных с ней понятий показы­вает, что в зависимости от стадии познания объекта, этапа систем­ного анализа в понятие цель вкладывают различные оттенки — от идеальных устремлений до конкретных целей-резуль­татов, достижимых в пределах некоторого интервала времени, формулируемых иногда даже в терминах конечного продукта деятельности.

Изучение взаимосвязей этих понятий показывает, что, в прин­ципе, поведение одной и той же системы может быть описано в терминах цели. и целевых функционалов, связывающих цели со средствами их достижения.

Для того чтобы отразить диалектическое противоречие, за­ключенное в понятии цель, в Большой Советской Энциклопе­дии дается следующее определение: цель — «заранее мыслимый результат сознательной деятельности человека»,воплощение замысла; подчер­кивается также, что понятие цели связано с человеком, его дея­тельностью, сознанием.

идеальные устремления

конечный результат

цель

Структуры, их виды и формы представления. Система может быть представлена простым перечислением элементов или «чер­ным ящиком» (моделью «вход-выход»). Однако чаще при исследо­вании объекта такого отображения недостаточно, так как требу­ется выяснить, что собой представляет объект, что в нем обеспечи­вает выполнение поставленной цели. В этих случаях систему ото­бражают путем расчленения на подсистемы, компоненты, элементы со взаимосвязями, которые могут носить различный характер, и вводят понятие структуры.

Структура(от латинского «structure», означающего строение, расположение, порядок) отражает определенные взаимосвязи, взаиморасположение составных частей системы, ее устройство (строение). При этом в сложных системах структура отражает не все элементы и связи между ними (в этом предельном случае, когда пытаются применить понятие структуры к простым, пол­ностью детерминированным объектам, понятия системы и струк­туры практически совпадают), а лишь наиболее существенные компоненты и связи, которые мало меняются при текущем функционировании системы и ее основных свойств. Иными словами, структура характеризует организованность системы, устойчивую упорядоченность ее элементов и связей.

Обычно понятие структура связывают с графическим отобра­жением. Однако это не обязательно. Структура может быть также представлена в матричной форме, в форме теоретико-множествен­ных описаний, с помощью языка топологии, алгебры и других средств моделирования систем.

Одна и та же система может быть представлена разными струк­турами в зависимости от стадии познания объекта или процесса аспекта их рассмотрения, цели создания. При этом в процессе исследования или проектирования структура системы может из­меняться. Структуры, особенно иерархические, как будет пока­зано ниже, могут помочь в раскрытии неопределенности сложных систем. Иными словами, структурные представления систем могут являться средством их исследования.

Различные виды структур имеют специфические особенности и могут рассматриваться как самостоятельные понятия теории систем и системного анализа. Кратко охарактеризуем основные из них.

вершины

1. Сетевая структура или сеть представляет собой декомпозицию системы во времени.

Например, сетевая структура может отображать порядок дей­ствия технической системы (телефонная сеть, электрическая сеть, т.п.), этапы деятельности человека (при производстве продук­ции — сетевой график, при проектировании - сетевая модель, при планировании — сетевая модель, при планировании — сете­вой план и т. д.).

При применении сетевых структур пользуются определенной терминологией:

вершина, ребро, путь, критический путь и т. д. Элементы сети могут быть рас­положены последовательно и параллельно. Сети бывают разные. Наиболее рас­пространены и удобны для анализа однонаправленные сети. Но могут быть и сети с обратными связями. Для анализа сложных сетей существует математиче­ский аппарат теории графов, прикладная теория сетевого планирования и управ­ления, что обусловливает их широкую распространенность при представлении процессов организации производства и управления предприятиями в целом.

2. Иерархические структуры представляют собой декомпозицию системы в пространстве. Все вершины (узлы) и связи (дуги, ребра) существуют в этих структурах одновре­менно (не разнесены во времени). Такие структуры могут иметь не два, а большее число уровней декомпозиции (структуризации).

Структуры типа а, в которых каждый элемент ниже­лежащего уровня подчинен одному узлу (одной вершине) вышеле­жащего ( и это справедливо для всех уровней иерархии), называют иерархическими структурами с «сильными» связями, древовидными,структурами типадерева.

Структура типа б, где элемент нижележащего уровня (один или несколько) может быть подчинен двум и более узлам (вершинам) вышележащего, называют иерархическими структурами со “слабыми” связями. В последнем случае отношения, имеющие вид слабых связей между уровнями, подобны отношениям в матрице, образованной из составляющих этих двух уровней.

б

а

Смешанные иерархические структуры (типа в) с вертикальными и горизонтальными связями, могут иметь как вертикальные связи разной силы (управление), так и горизонтальные связи взаимодействия (координация).

в

3. Структуры с произвольными связями – используются на начальном этапе познания системы, когда не известен характер взаимодействий между элементами и распределение элементов по уровням иерархии.

4. Матричные структуры – соответствуют взаимоотношениям между двумя смежными уровнями иерархической структуры со “слабыми” связями. Матричные структуры могут быть и многомерными.

	1.1
	1.2
	1.3
	2.1
	2.2

1.1	+	+
1.2	+
1.3	+
2.1	+	+
2.2		+

Понятия, характеризующие функционирование и развитие систем. Изменения и преобразования, происходящие в сложных системах, как правило, сразу не удается представить в виде мате­матических соотношений или хотя бы алгоритмов. Поэтому для того, чтобы хоть как-то охарактеризовать стабильную ситуацию или ее изменения, используются специальные термины, заимст­вованные теорией систем из теории автоматического регулиро­вания, биологии, философии. Рассмотрим основные из этих терминов.

Состояние. Понятием состояние обычно характеризуют мгновенную фотографию, ”срез” системы, остановку вее развитии. Его определяют либо через входные воздействия н выходные сиг­налы (результаты), либо через макропараметры, макросвойства системы (давление, скорость, ускорение). Так, говорят о состоя­нии покоя (стабильные входные воздействия и выходные сигналы), о состоянии равномерного прямолинейного движения (стабиль­ная скорость) и т. д.

Если, рассматривая элементы ε (компоненты, функциональные блоки), учесть, что “входы” можно разделить на управляющие у и возмущающие x (не­контролируемые) и что «выходы» (выходные результаты) зависят от ε, у и x, т. е. g = f (ε, у, х), то в зависимости от задачи состояние может быть определено как {ε, у} (управляющая система), {ε, у, g} (процесс управления) или {ε, у. х, g} (система).

	x			g

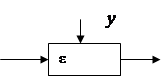Поведение. Если система способна переходить из одного состояния в другие (например, s₁ s₂ s₃) то говорят, что она обладает поведением. Этим понятием пользуются, когда неизвестны закономерности (правила) перехода из одного состояния в другое. Тогда говорят, что система обладает каким-то поведением и вы­ясняют его характер, алгоритм. С учетом введенных обозначений поведение можно представить как функцию S _t = f (s _t-1, y _t, x _t).

Равновесие. Понятие равновесиеопределяют как способ­ность системы в отсутствии внешних возмущающих воздействий (или при постоянных воздействиях) сохранять свое поведение сколь угодно долго.

Устойчивость.Под устойчивостью понимают спо­собность системы возвращаться в состояние равновесия после того, как она была из этого состояния выведена под влиянием внешних возмущающих воздействий (например, внешних, экономических или социальных конфликтов). Эта способность обычно присуща си­стемам при постоянном у только тогда, когда отклонения не пре­вышают некоторого предела.

Состояние равновесия, в которое система способна возвра­щаться, называют устойчивым состоянием равновесия. Возврат в это состояние может сопровождаться колебательным процессом. Соответственно в сложных системах возможны неустойчивые состояния равновесия.

неустойчивое равновесие

		t

регресс

прогресс

развитие

Развитие. Это понятие помогает объяснить сложные тер­модинамические и информационные процессы в природе и обще­стве. Исследованию процесса развития, соотношению развития и устойчивости, изучению механизмов, лежащих в их основе, уде­ляют все больше внимания.