Негізгі тригонометриялық теңбе-теңдіктер

α сүйір бұрышының әрбір мәніне сәйкес sinα-ның, cosα-ның, tgα-ның және ctgα-ның мәндерін анықтауға болады.

1. Катеттері а мен b, гипотенузасы с болатын, ал сүйір бұрыштары α мен β-ға тең АВС тік бұрышты үшбұрышы берілсін. Пифагор теоремасын жазамыз:

a²+b²=c² (*)

§8, (1) және (2) формулалардан b=ccosα, a=csinα болатыны белгілі. Осы мәндерді (*) –ға қойсақ,

sin²α+cos²α=1 (1)

шығады. Бұл α бұрышының синусы мен косинусын байланыстыратын теңбе-теңдік.

2. Берілген тікбұрышты үшбұрыш үшін

ctgα=

болатыны белгілі. Бұл теңдіктерге b=ccosα, a=csinα мәндерін қойсақ,

(2)

(3)

Аламыз. Бұл теңдіктер кез-келген α сүйір бұрышы үшін орындалатын теңбе-теңдік болып саналады.

3. (1) тепе-теңдік әрбір мүшесін сos²α-ға немесе sin²α-ға бөліп, төмендегідей екі тепе-теңдікті алуға болады:

1+tg²α= (4)

1+ctg²α= (5)

4. АВС тікбұрышты үшбұрышына сүйір бұрыштар үшін α+β=90⁰ өрнегі Бұдан β=90⁰-α. 30-суреттен sin= 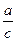, ал cosβ= 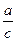сондықтан cos(90⁰-α). Сонда

cos(90⁰-α) =sinα (6)

теңбе-теңдігін аламыз. Осы сияқты

sin(90⁰-α)=cosα (7)

теңбе-теңдігін алуға болады.

Есептер шығару

Оқулықпен жұмыс

№144. Өрнекті ықшамдаңдар

1) 2+sin²α+cos²α=2+1=3

2) (1 – sinα )(1+sinα)=1-sin²α=cos²α

№145.

1) (1+ctg²α)∙sin²α+1=

2) tgα∙ctgα+sinα=1+sinα

4. Үйге тапсырма: §10 №144 (2), 145 (2)

Орытындылау

Слайд 1.sin²α+cos²α=1

2. 5. 1+ctg²α=

3. 6. cos(90⁰-α) =sinα

4. 1+tg²α= 7. sin(90⁰-α)=cosα

30-сабақ

Сабақтың тақырыбы:Есептер шығару

Сабақтың мақсаты:

Білімділік:Негізгі тригонометриялық теңбе – теңдіктерді есептер шығаруда, теңбе-теңдіктерді дәлелдеуде қолдана білу..

Дамытушылық:Оқушылардың ой өрісін, есте сақтау, сызбамен жұмыс істеу қабілеттерін, дағдыларын дамыту.

Тәрбиелік:Оқушыларды ұқыптылыққа, шыдамдылыққа, нәтиже алуға баулу.

Сабақ түрі:Практикалық сабақ

Көрнекілігі: интерактивті тақта, слайд, есептер жинағы

Сабақтың барысы: 1. Ұйымдастыру кезеңі

2. Үй тапсырмасын сұрау

3. Есептер шығару

(1)-(7) теңбе-теңдіктерді қолданып №146-148 есептерді шығарамыз:

№146 α<90⁰ үшін (2tg²α∙cos²α+2cos² α)∙sin α+3sin α=5sin α тепе-теңдігін дәлелдеңдер.

Шешуі: (2tg²α∙cos²α+2cos² α)∙sin α+3sinα=2cos²α(tg² α+1)∙sin α+3sin α=2cos² α∙ ∙ sin α+3sin α=2sin α+3sin α=5sin α

5sin α=5sin α

№148. α<90⁰ үшін 1) tg (90^0- α)=ctg α

tg α= , sin(90⁰-α)=cosα , cos(90⁰-α) =sinα

tg90= =

ctg α= ctg α дәлелденді.

№149. α<90⁰ үшін sinα-ны, cosα-ны, tg α-ны, ctg α-ны анықтаңдар

1) cos² α=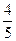

2) Шешуі: sin α=

tgα= = : ctgα= = =

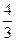
3) cosα=0.8

sin α= = =

tgα= = , ctgα=

Қорытындылау. 1-слайд

Шешуі: Өрнекті ықшамдаңдар.

2-слайд

Өрнекті ықшамдаңдар:

3-слайд.

Өрнектерді ықшамдаңдар

Үйге тапсыра: №147, 148,(2),149 (2)

31-сабақ

Сабақтың тақырыбы:§11. 30⁰, 45⁰ және 60⁰ бұрыштары үшін синустың, косинустың, тангенстің және котангенстің мәндері.

Сабақтың мақсаты:

Білімділік:α бұрышы 30⁰, 45⁰, 60⁰-қа тең болғанда cosα, sinα, tgα,ctga –ның кестелік мндерін білу, біреуінің мәні бойынша қалғандарын есептеу, тригонометриялық теңбе-теңдіктерді және 30⁰, 45⁰, 60⁰ т.б. бұрыштар үшін синус, косинус, тангенс, котангенс кестесін есептер шығаруда қолдана білу.

Дамытушылық:Оқушылардың ой өрісін, есте сақтау, сызбамен жұмыс істеу қабілеттерін, дағдыларын дамыту.

Тәрбиелік:Оқушыларды ұқыптылыққа, шыдамдылыққа, нәтиже алуға баулу.

Сабақ түрі:Жаңа білімді игеру

Көрнекілігі: интерактивті тақта, слайд, есептер жинағы

Сабақтың барысы: 1. Ұйымдастыру кезеңі

2. Үй тапсырмасын сұрау: № 147, 148(2), 149 (2)

3. Жаңа сабақты баяндау.

§11. 30⁰, 45⁰ және 60⁰ бұрыштары үшін синустың, косинустың, тангенстің