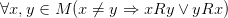Нормальные формы формул К-значной логики.

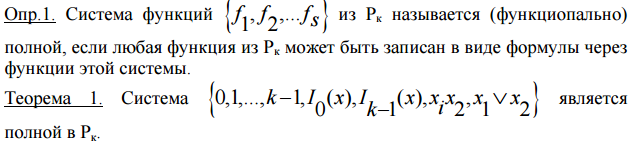
10. Множества, декартово произведение множеств. Отношения. Основные свойства отношений. Графическое задание бинарных отношений.

Множество – это совокупность определенных объектов, которые могут иметь конкретные свойства.

Множество состоит из отдельных объектов – элементов множества.

Множество обозначается большими буквами латинского алфавита, а его элементы – маленькими буквами латинского алфавита. Множества записываются в фигурных скобках (X={a,b})

Принято использовать следующие обозначения:

· a∈ X — символ принадлежности, читается как «элемент a принадлежит множеству X»;

· a∉ X— символ отрицания принадлежности, читается как«элемент aa не принадлежит множеству X»;

· ∀ — квантор произвольности, общности, читается как «любой» или «какой бы не был», или «для всех»;

· ∃— квантор существования, например, ∃ y∈ B— «существует (найдется) элемент y из множества B»;

· ∃!— квантор существования и единственности, например, ∃! b∈ C— «существует единственный элемент b из множества C»;

· :— символ пояснения, читается как «такой, что« или «обладающий свойством»;

· ⇒— символ следствия, читается как отсюда следует или отсюда вытекает;

· ⇔ — квантор эквивалентности, равносильности, читается как «тогда и только тогда».

Конечное множество – это множество, которое состоит из конечного числа элементов. Например, множество букв английского алфавита — представляет собой конечное множество.
Бесконечное множество – множество, которое состоит из бесконечного числа элементов. Например, множество рациональных чисел — представляет собой бесконечное множество.

Мощность множества – это число элементов, которое содержится в конечном множества |A|.

Пустое множество — это множество, которое не содержит ни одного элемента

Равные множества – это множества, которые включают в себя одни и те же элементы, то есть являются эквивалентными по отношению друг к другу.

Множества X и Y называются не равными (X≠ Y), если множество X содержит в себе элементы, которые не содержит в себе множество Y. Другими словами – множество X имеет элементы, которые не принадлежат множеству Y.

Декартовым (или прямым) произведением множествA и B называется такое результирующее множество пар вида (x,y), построенных таким образом, что первый элемент из множества A, а второй элемент пары — из множества B. Общепринятое обозначение:

A×B={(x,y)|x∈A,y∈B}

Произведения трёх и более множеств можно построить следующим образом:

A×B×C={(x,y,z)|x∈A,y∈B,z∈C}

Произведения вида A×A, A×A×A,A×A×A×A и т.д. принято записывать в виде степени: A2,A3,A4 (основание степени — множество-множитель, показатель — количество произведений). Читают такую запись как «декартов квадрат» (куб и т.д.)

Бинарные отношения

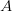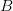Пусть и два конечных множества. Декартовым произведением множеств 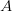и 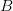называют множество 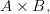состоящее из всех упорядоченных пар, где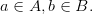

Бинарным отношением между элементами множества 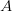и 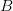называется любое подмножество 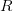множества 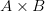, то есть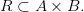

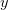По определению, бинарным отношением называется множество пар. Если R – бинарное отношение (т.е. множество пар), то говорят, что параметры и связаны бинарным отношением 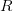, если пара 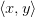является элементом R, т.е.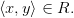

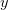Высказывание: “предметы и связаны бинарным отношением 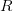” записывают в виде 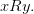Таким образом,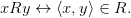

Если 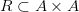, то говорят, что бинарное отношение определено на множестве .

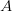Областью определения бинарного отношения 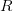называется множество, состоящее из таких , для которых 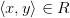хотя бы для одного .

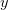Область определения бинарного отношения будем обозначать .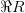

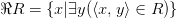
Областью значений бинарного отношения 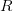называется множество, состоящее из таких 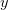, для которых 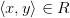хотя бы для одного .
Область значений бинарного отношения будем обозначать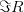

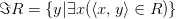
Инверсия (обратное отношение) 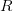— это множество и обозначается, как

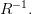
Композиция (суперпозиция) бинарных отношени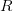й и 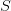— это множество 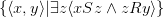и обозначается, как .

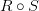Свойства бинарных отношений

Бинарное отношение 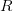на некотором множестве 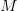может обладать различными свойствами, например:

· Рефлексивность: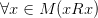

· Антирефлексивность (иррефлексивность):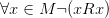

· Корефлексивность: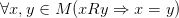

· Симметричность: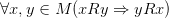

· Антисимметричность: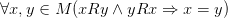

· Асимметричность: 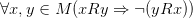. Асимметричность эквивалентна одновременнойантирефлексивности и антисимметричности отношения.

· Транзитивность: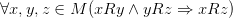

· Связность: