ТЕОРЕМА (О разложении булевой функции по переменным)

F (x1,…, xm, x m+1,…,xn)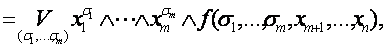

где дизъюнкция берется по всем возможным наборам (s₁,…,s_м).

ДОКАЗАТЕЛЬСТВО

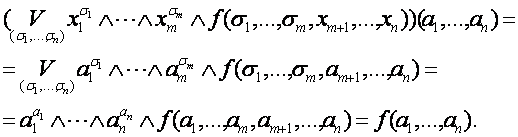ЗАМЕЧАНИЕ

Здесь доказывается, что некоторая формула реализует заданную функцию. Для этого до­статочно взять произвольный набор значений аргументов функции, вычислить на этомнаборе значение формулы, и если оно окажется равным значению функции на этом на­боре аргументов, то из этого следует доказываемое утверждение.

Дизъюктивные и конъюнктивные нормальные формы формул. Совершенные формы формул

Дизъюнкти́внаянорма́льнаяфо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любаябулева формула может быть приведена к ДНФ.^[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Пример ДНФ: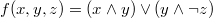

Конъюнкти́внаянорма́льнаяфо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.^[1] Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.

Пример КНФ: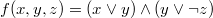

Совершенная конъюнктивная нормальная форма, СКНФ (англ. perfectconjunctivenormalform, PCNF) — это такая КНФ, которая удовлетворяет условиям: § в ней нет одинаковых простых дизъюнкций § каждая простая дизъюнкция полная

Пример СКНФ: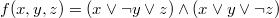

Соверше́ннаядизъюнкти́внаянорма́льнаяфо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:

· в ней нет одинаковых элементарных конъюнкций

· в каждой конъюнкции нет одинаковых пропозициональных букв

· каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.

Любая булева формула, не являющаяся тождественно ложной, может быть приведена к СДНФ, причем единственным образом^[1], то есть для любой выполнимой функции алгебры логики существует своя СДНФ, причём единственная.

Совершенная ДНФ этой функции:

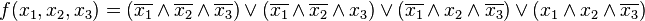
Полнота систем логических функций. Пример полных систем. Свойства линейности , двойственности и монотонности логических функций

Полнота систем логических функций и пример

Определение. Множество функций N называется функционально полной системой (ФПС), если любая булева функция представима суперпозицией функций из N.

Договоримся опускать аргументы при перечислении функций множества N и рассматривать термин ''система'' в данном контексте как синоним множества.

Пример 1. Множество N₁={ 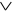, , 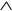^–} является функционально полной системой, так как любую булеву функцию, кроме константы 0, можно представить совершенной ДНФ, то есть суперпозицией функций из N₁ а константу 0 – формулой xx . •

Пример 2. Множество N₂={ 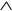, , 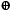1} является ФПС, так как любую булеву функцию можно представить полиномом Жегалкина, то есть суперпозицией функций из N₂, а полином 0 – формулой 1 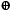1. •

Следующая теорема позволяет сводить вопрос о функциональной полноте одних систем к вопросу о полноте других систем.

Теорема о двух функционально полных системах. Если даны два множества N₁ и N₂ булевых функций и известно, что N₁ – функционально полная система, а каждая функция из N₁ представима суперпозицией функций из N₂, то N₂тоже является функционально полной системой.

Доказательство. Рассмотрим произвольную булеву функцию f(x₁, …, x_n). Она может быть представлена суперпозицией функций из множества N₁={f₀,f₁…, f_m}, так как N₁ – ФПС:

f(x₁, …, x_n)=f₀(f₁(x₁, …, x_n), …, f_m(x₁, …, x_n)).

По условию теоремы каждая из функций f₀, f₁ …, f_m может быть представлена суперпозицией функций из N₂, значит, функция f(x₁, …, x_n) представима суперпозицией функций из N₂, следовательно, N₂ – ФПС. •

Пример 1. N₁={ 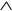, 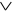^–, }, N₂={ 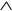, ^–}. Как показано ранее, N₁ – ФПС. Конъюнкция и инверсия содержатся в N₂, а дизъюнкция представима суперпозицией функций из N₂: x 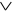y = 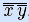, значит, N₂ – ФПС. •

Пример 2. N₁={ 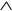, ^–}, N₂={↓ }. Как показано в предыдущем примере, N₁ – ФПС. Инверсия и конъюнкция могут быть представлены суперпозицией стрелки Пирса: x = x↓ x, xy = 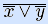= (x↓ x)↓ (y↓ y), следовательно N₂ – ФПС. •

Двойственная функци

Пусть имеем функцию f(a,b,c). Двойственной для нее является функцияf*= 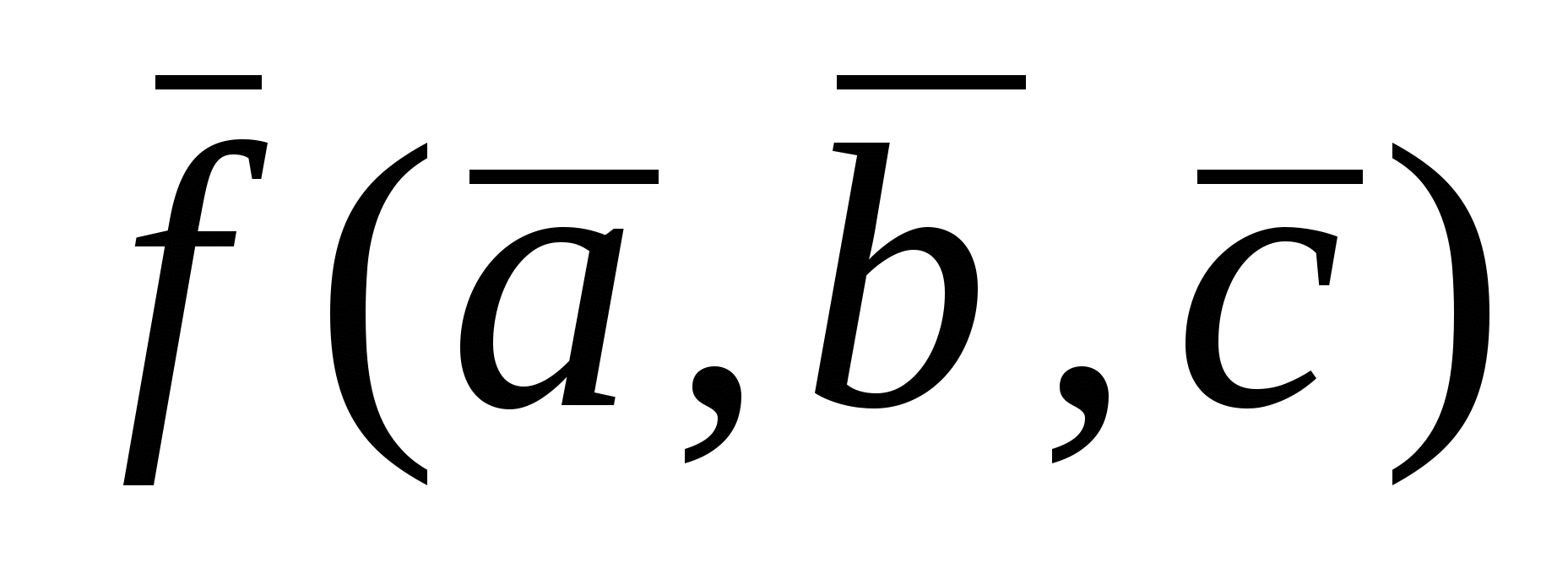, т.е. функция, в которой все аргументы и сама функция инвертированы.

Пример 2:

;

;

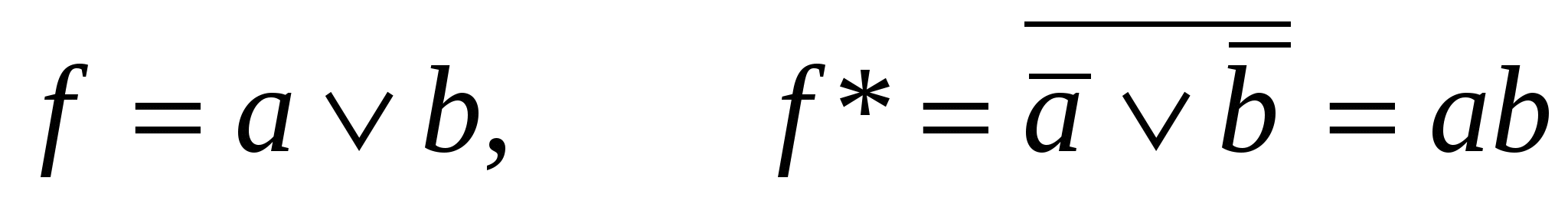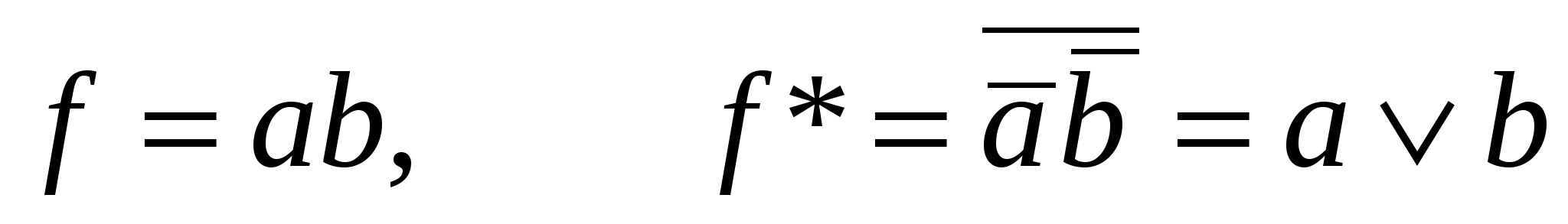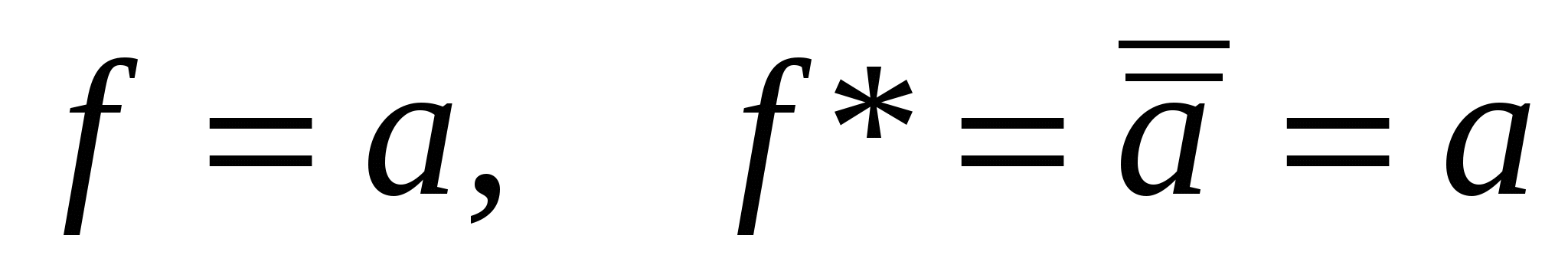– самодвойственная функция;

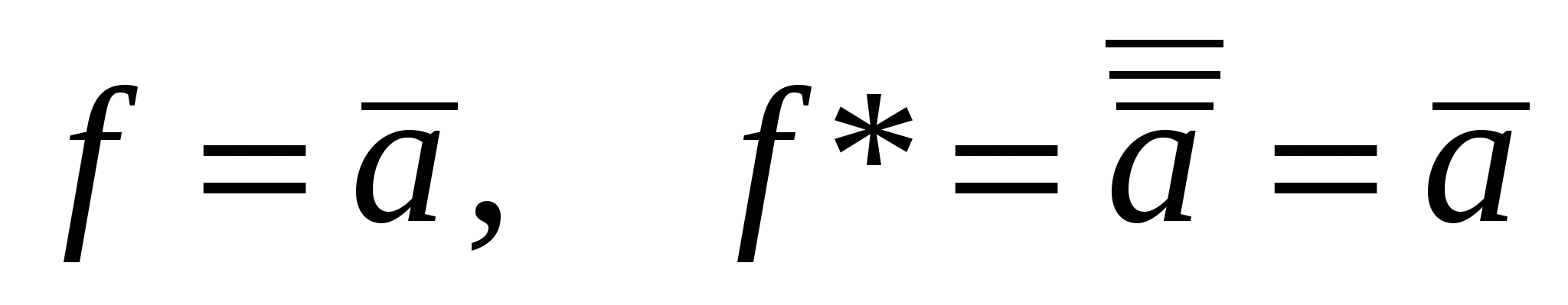– самодвойственная функция;

, = = =

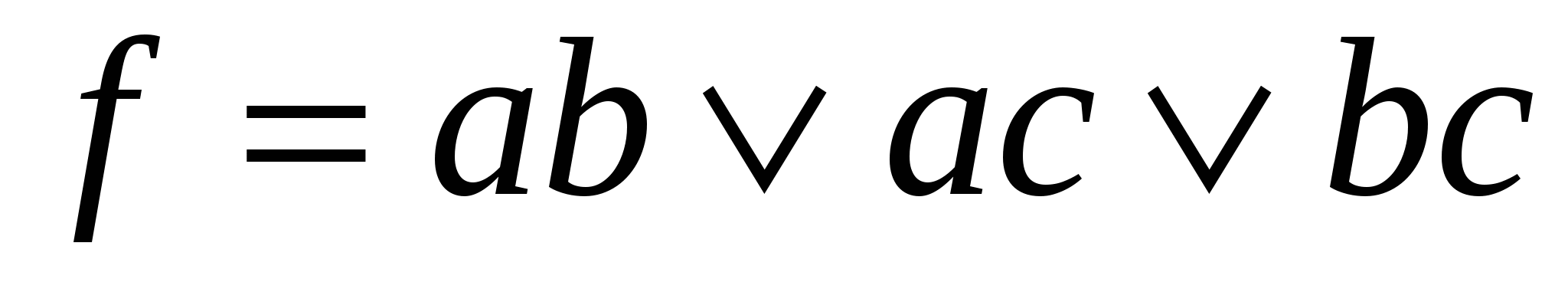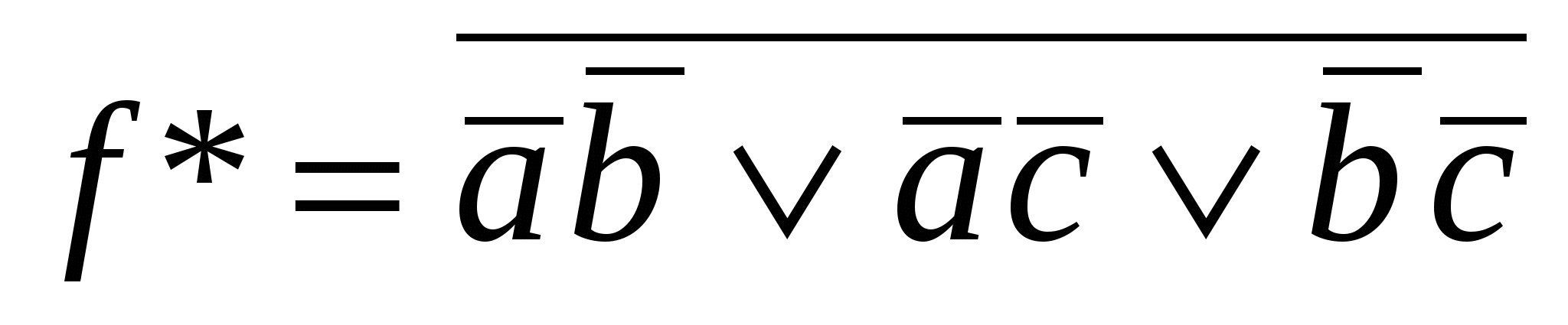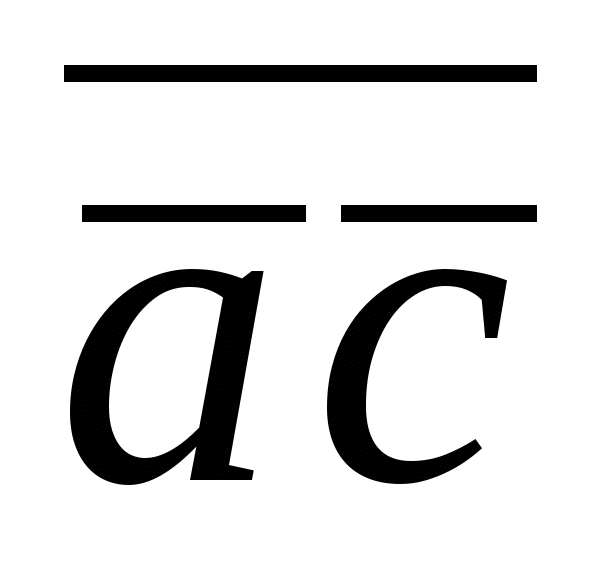
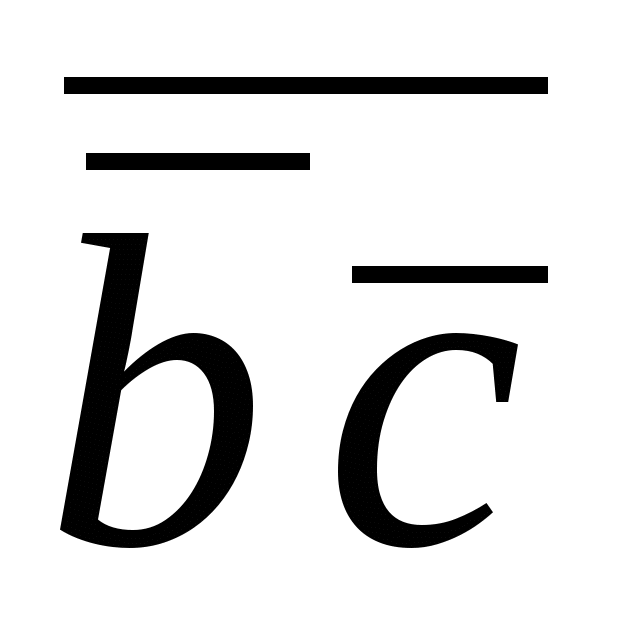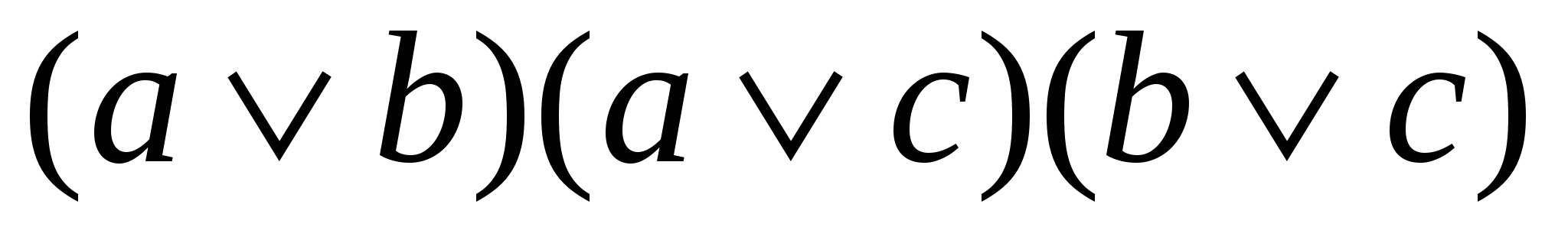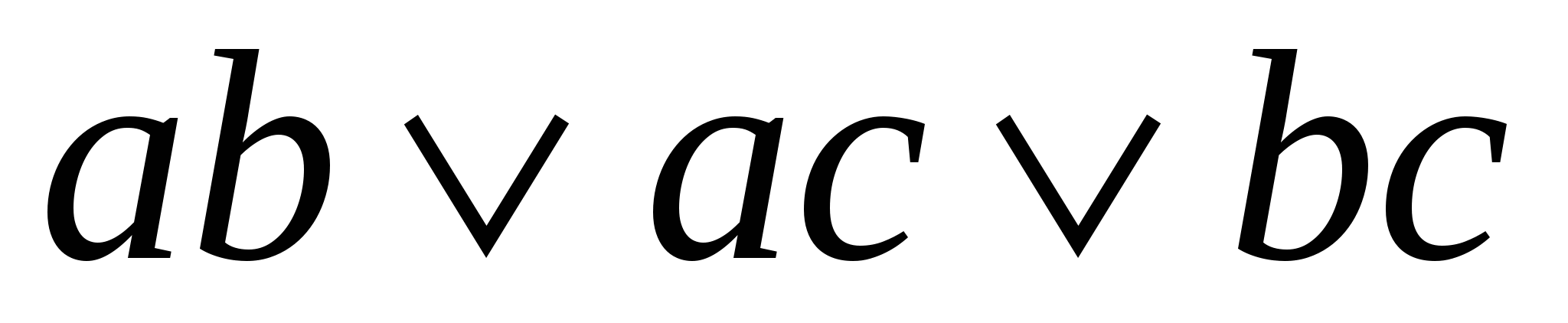= – самодвойственная функция.

Таким образом, для самодвойственной функции можно записать

f(a,b,c) = .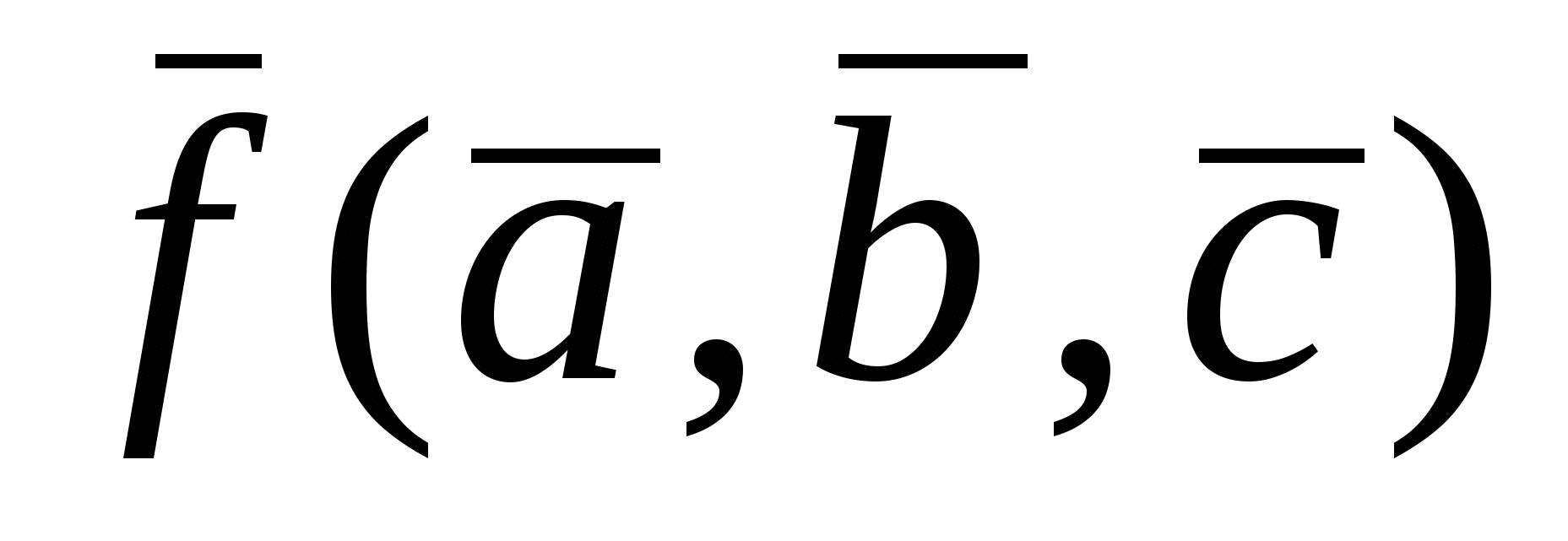

Монотонная функция

Выше мы установили для входных наборов отношение предшествования: Входной набор 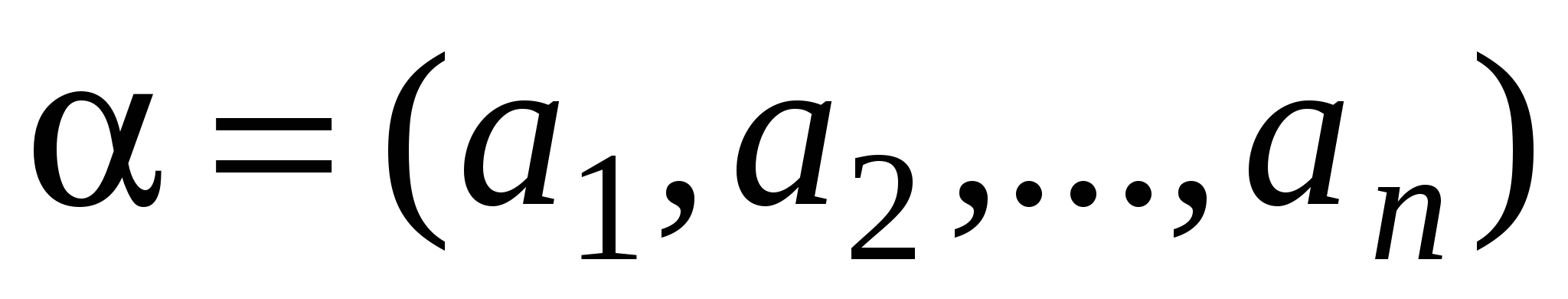предшествует набору 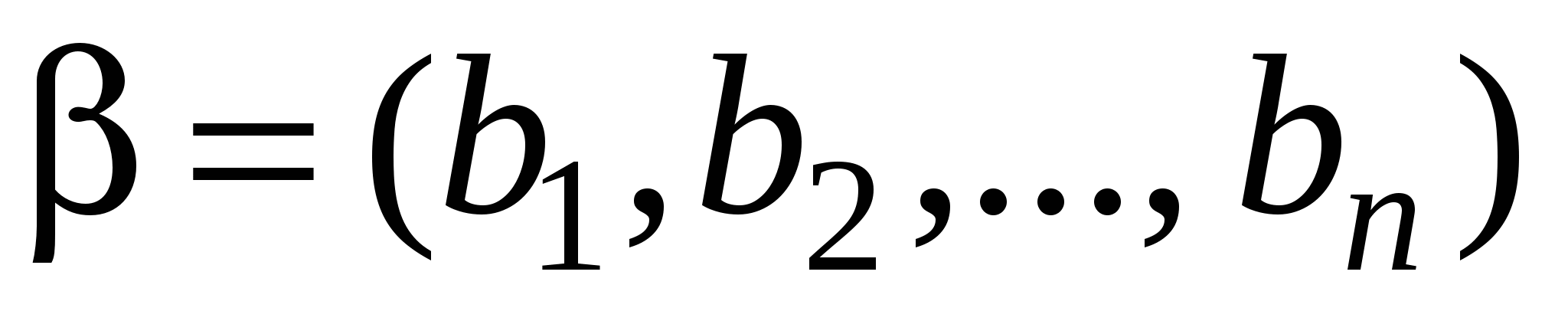(обозначается это так 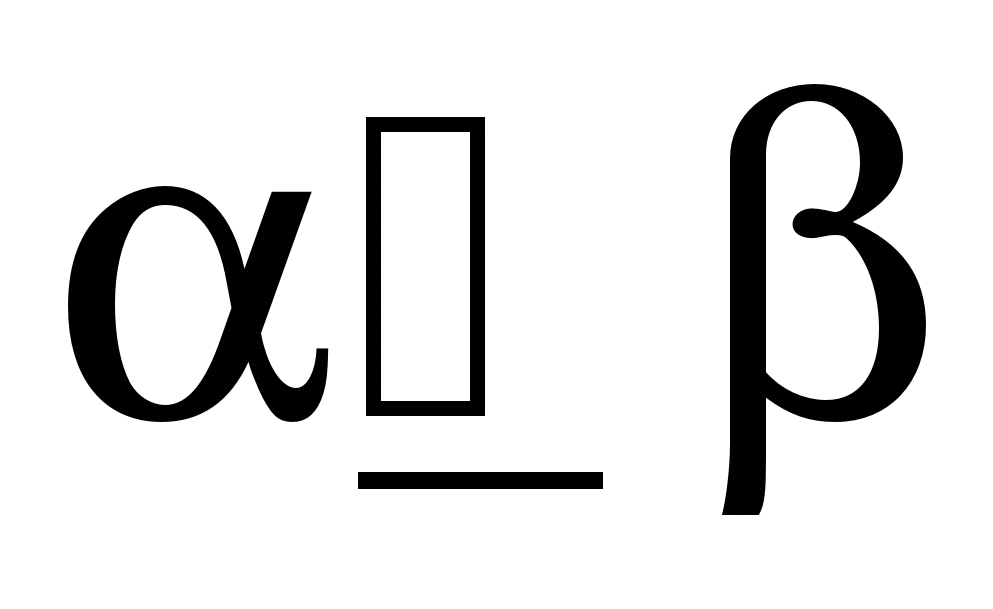), если .

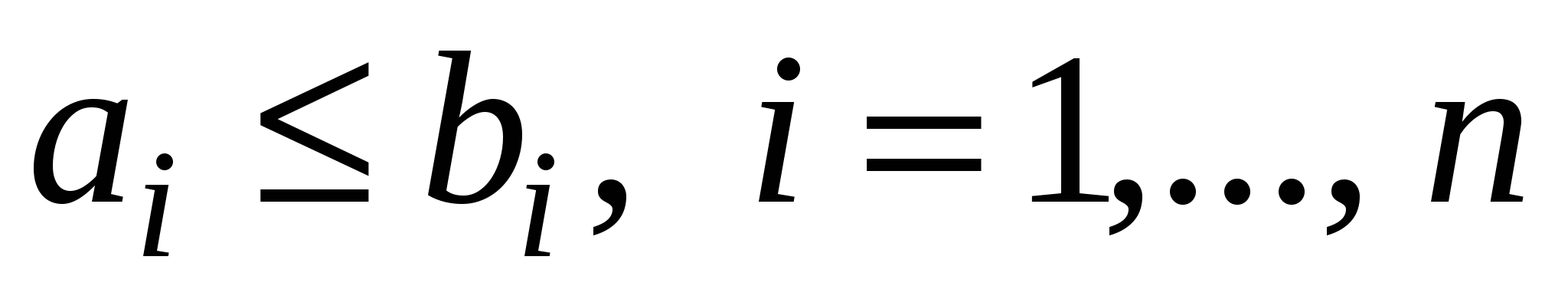функция 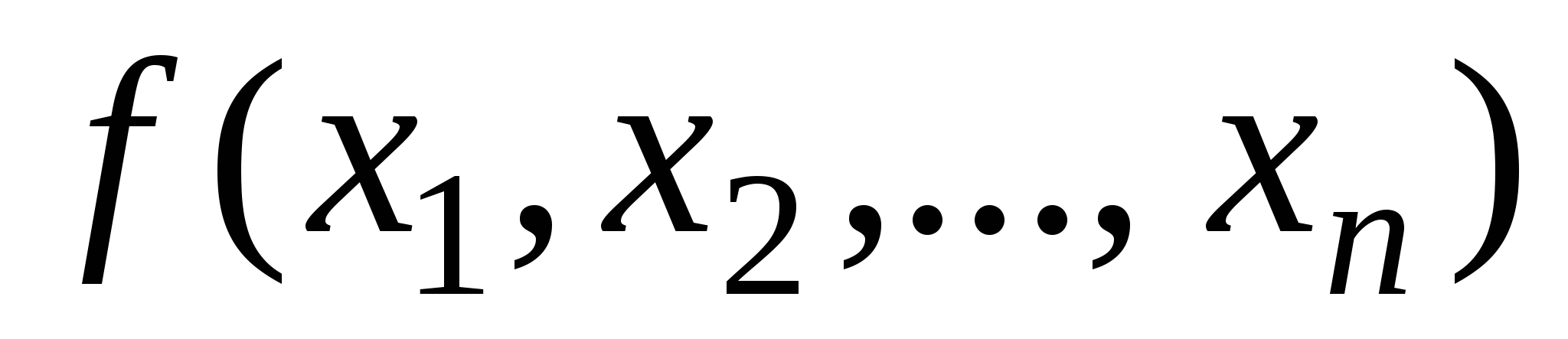монотонна, если для любых двух наборов таких, что они отвечают условиям , имеет место .

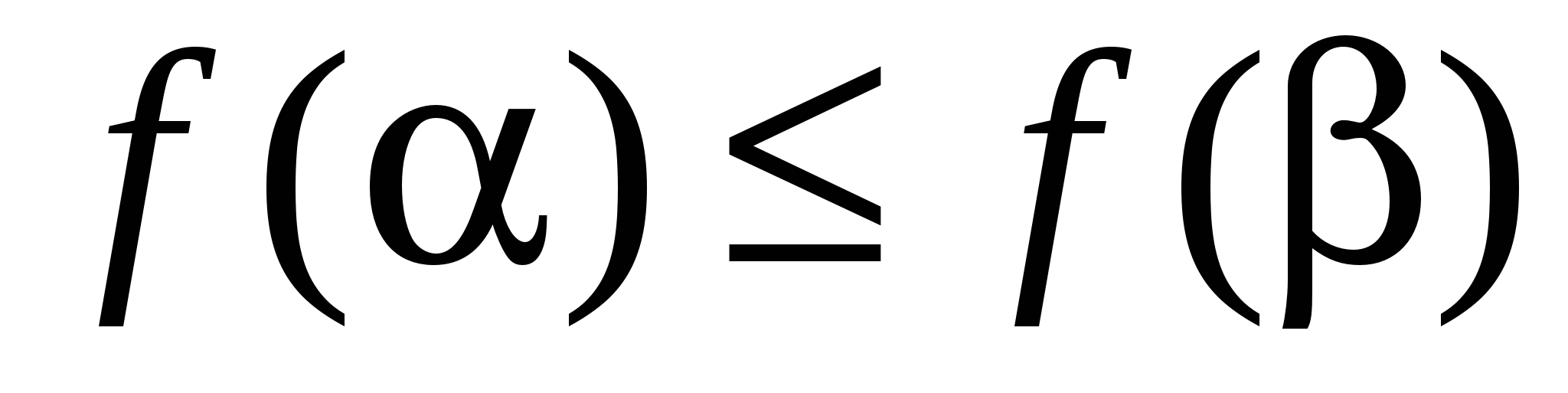Если хотя бы для одной пары таких наборов это не выполняется, то функция не монотонна. Например, функции 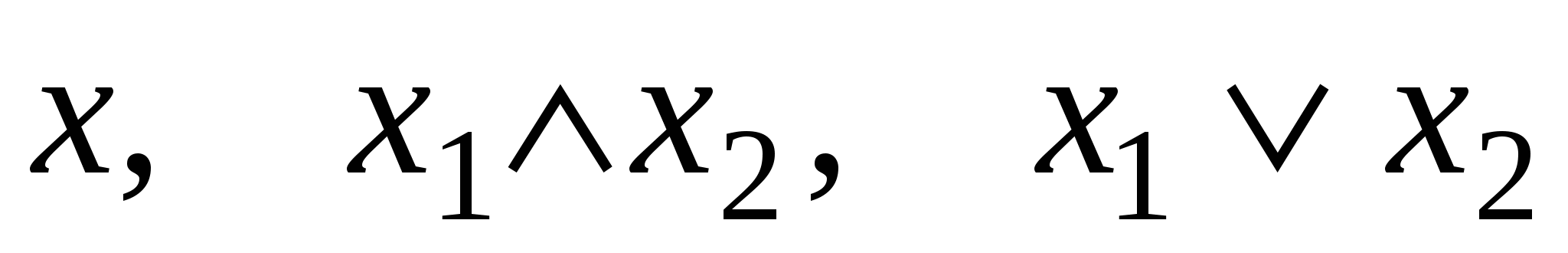монотонны, а функция 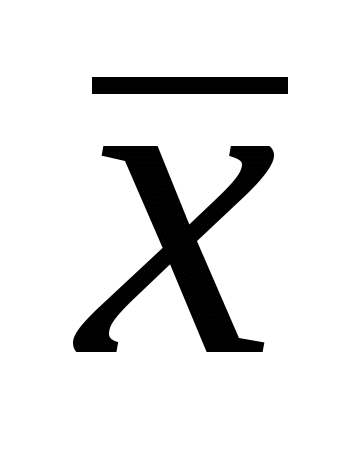не монотонна.

Замечание:Любая монотонная логическая функция может быть представлена в форме без инверсий.

Линейная функция

Функция называется линейной, если ее можно представить полиномом Жегалкина в виде суммы по модулю 2 константы a₀и переменныхx_i, умноженных на постоянные коэффициенты:

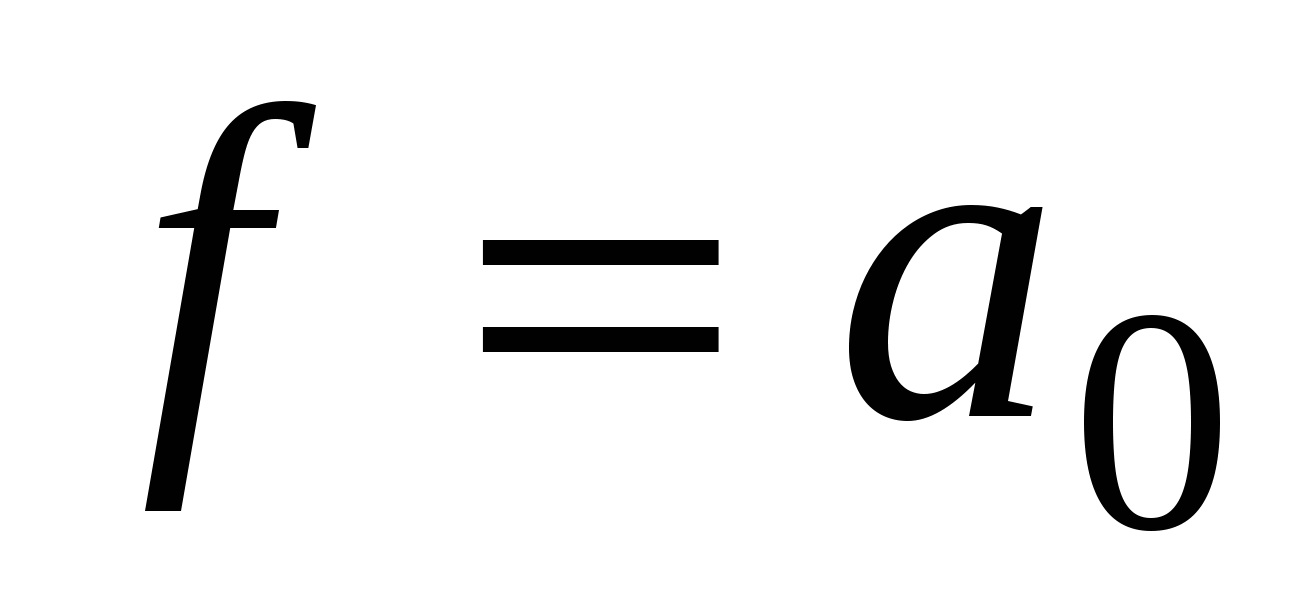
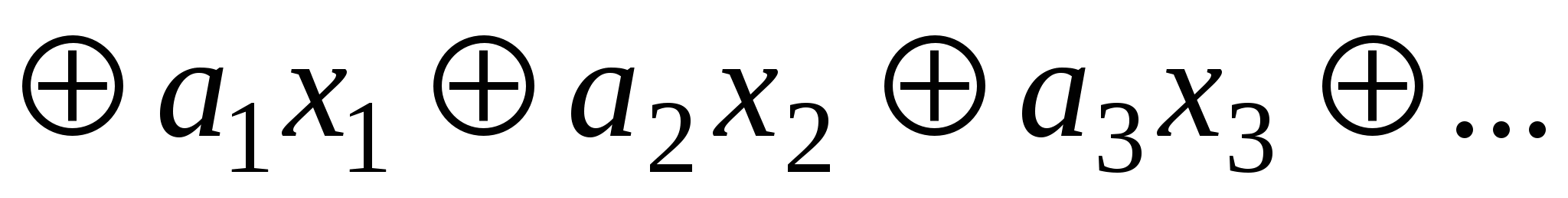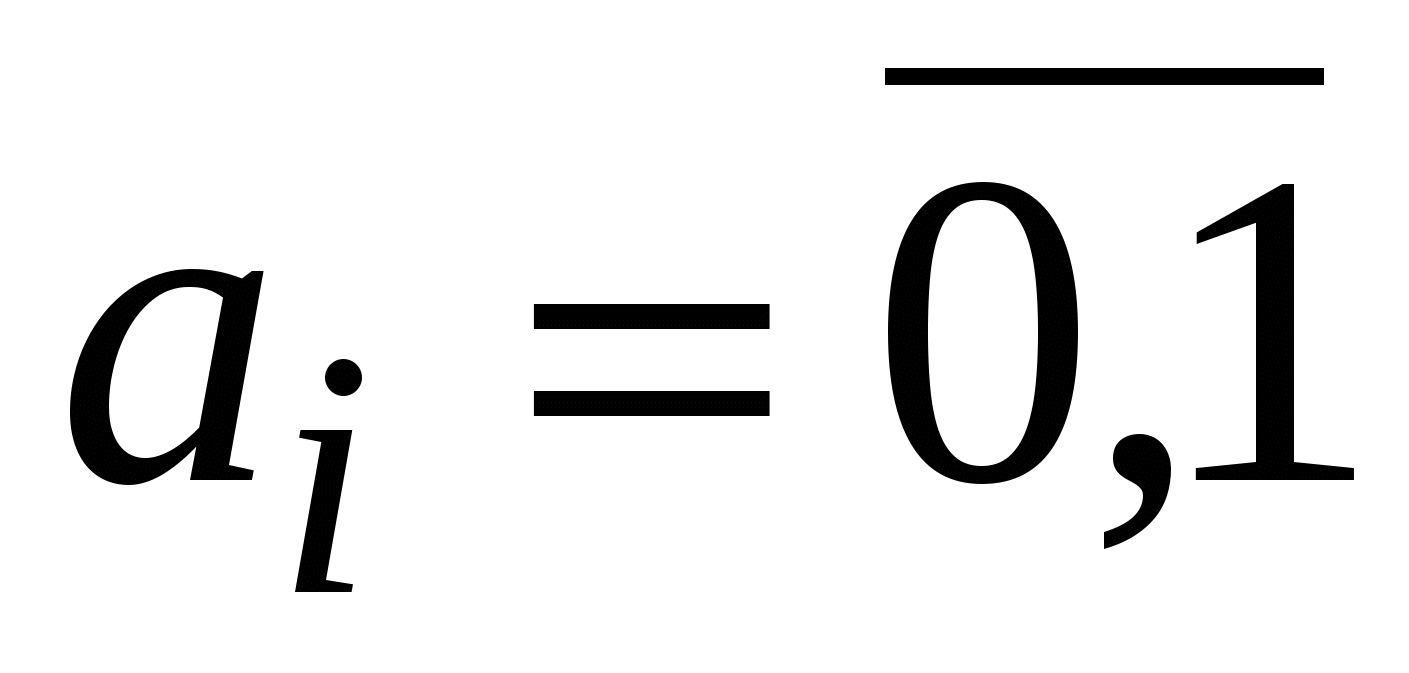, – линейная функция.

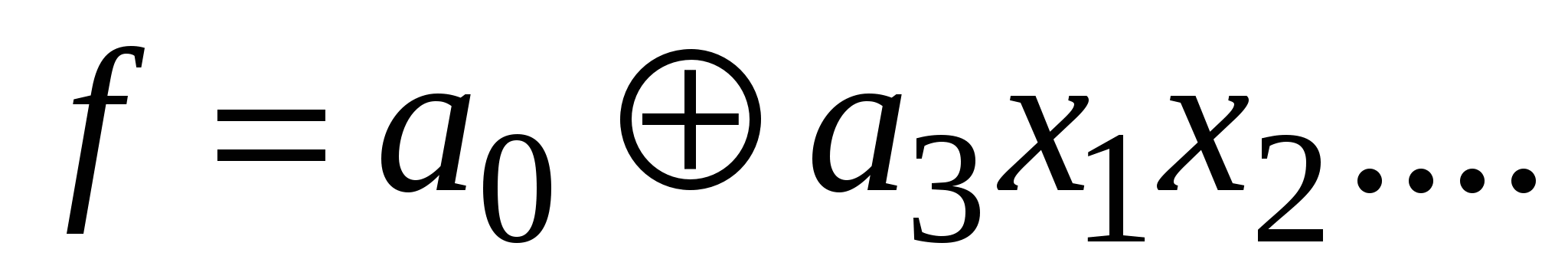– нелинейная функция, так как есть произведение переменных.

5. Понятие замкнутости систем логических функций. Замкнутость классов Т₀, Т_1, L, S, M.

Класс логических функций (множество логических функций) называется замкнутым, если любая суперпозиция функций этого класса снова будет функцией этого же класса. Основными замкнутыми классами логических функций являются классы линейных, самодвойственных, монотонных, сохраняющих константу 0 и 1 функций. Эти классы имеют специальные обозначения и обозначаются соответственно: L, S, M, T0, T1. При помощи основных замкнутых классов логических функций можно установить полноту систем логических функций,