Предикаты и операции с ними. Формулы.

Опр.Пусть M ¹ Æ. Назовём n-местным предикатом, заданным на M выражение, содержащее n переменных, обращающееся в высказывание при замене переменных элементами из M.

Обозначение: .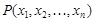

Опр. Назовём нульместным предикатом высказывание.

Операции с высказываниями переносятся на предикаты:

конъюнкция, дизъюнкция, отрицание, импликация, эквиваленция.

Например, для конъюнкции новое определение формулируется так:

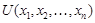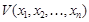Опр. Пусть и n-местные предикаты, заданные на M. Конъюнкцией этих предикатов называется новый предикат 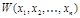, такой, что для любых элементов 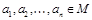высказывание .

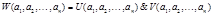Кроме этих пяти операций введём ещё две операции навешивания кванторов.

Опр. Пусть 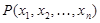- n-местный предикат, заданный на M, y - переменная (либо совпадающая с 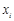, либо новая). Назовём предикатом, полученным навешиванием квантора общности на 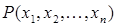выражение «Для любого y выполняется ».

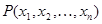Обозначение: .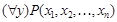

Опр. Пусть 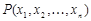- n-местный предикат, заданный на M, y - переменная (либо совпадающая с 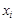, либо новая). Назовём предикатом, полученным навешиванием квантора существования на 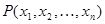выражение «Существует y, такой, что выполняется ».

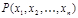Обозначение: .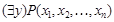

Опр. Термом называется выражение одного из двух видов:

1) переменная или константа (символ нуль-местной функции);

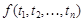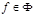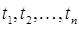2) , где , - термы.

Опр. Атомарной формулой называется выражение

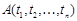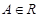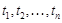, где , - термы.

Опр. Формулой логики предикатов называется выражение одного из двух видов:

1) атомарная формула;

2) (F) & (G), (F) Ú (G), Ø(F), (F) ® (G), (F) « (G), ("y)(F), ($y)(F),

где F и G - формулы логики предикатов, y - переменная.

Опр. В формулах ("y)(F), ($y)(F), формула F называется областью действия квантора по переменной y.

Для уменьшения количества скобок договоримся о приоритетах операций: у кванторов выше, чем у связок, для связок также, как в высказывания.

Интерпретация, равносильность. Законы логики предикатов. Логическое следствие.

Опр. Вхождение переменной в формулу называется связанным, если переменная стоит непосредственно за квантором, или входит в область действия квантора по этой переменной.

Вхождение переменной свободное - в противном случае.

Опр. Переменная называется свободной в формуле, если существует хотя бы одно свободное вхождение этой переменной в формулу.

Пример. .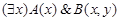

Опр. Интерпретацией формулы F на непустом множестве M называется отображение j, ставящее в соответствие:

символу константы - элемент из M,

символу n-местной функции f - некоторую функцию на M,

символу n-местного предиката A - некоторый предикат, заданный на M.

Результатом j(F) интерпретации формулы является предикат 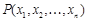, где переменные 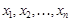являются свободными в формуле F.

Опр. Формулы 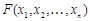и 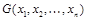называются равносильными, если для любой интерпретации 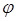на множестве M, и любых элементов 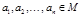, значения истинности высказывани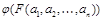й и 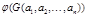совпадают.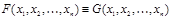

Опр. Формула 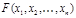называется тождественно истинной, если для любой интерпретации 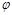на множестве M, и любых элементов 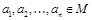, высказывание 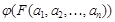истинно.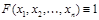

Теорема.

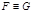Û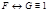

Законы логики предикатов:

1) - 21) аналогичны законам логики высказываний.

22) ;

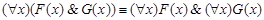23) ;

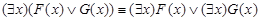Замечание:

1. .

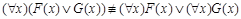Для доказательства неравносильности можно привести контрпример.

Пусть 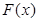= «Число x чётное», 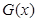= «Число x нёчетное» - одноместные предикаты на N.

Тогда и левая часть и правая часть равенства являются высказываниями:

л.ч. = «Для любого натурального числа x выполняется, что x чётное или x нечётное» = 1;

п.ч. = «Любое натуральное число чётное или любое натуральное число нечётное» = 0 Ú 0 = 0.

2. ;

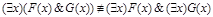Доказательством служит такая же интерпретация, как в предыдущем случае.л.ч. = «Существует натуральное число x, такое, что выполняется x чётное и x нечётное» = 0;

п.ч. = «Существует натуральное число чётное и существует натуральное число нечётное» = 1 & 1 = 1.

24) ;

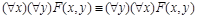25) ;

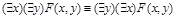Замечание: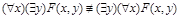

Для доказательства неравносильности можно привести контрпример.

Пусть 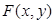= « x £ y » - двухместный предикат на N.

л.ч. = «Для любого числа x существует y, превышающий или равный x» = 1.

п.ч. = «Существует число y, такое, что для любого x выполняется x £ y» = 0.

26) ;

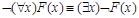27) ;

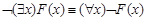28) ;

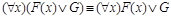29) ;

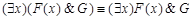Пусть 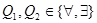, 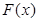не содержит y, 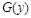не содержит x.

30) ;

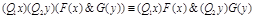31) ;

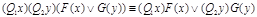32) ;

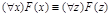33) .

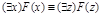Опр. Формула 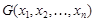называется логическим следствием формул 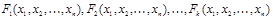, если для любой интерпретации 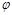на множестве M, и любых элементов 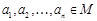, из того, что все значения 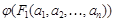, …, 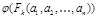истинны, следует, что значение 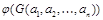истинно.

9. Нормальные формы в логике предикатов

Опр. Формула F имеет предварённую нормальную форму (ПНФ), если 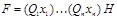, где 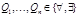, H не содержит кванторов.

Теорема.

Для всякой формулы F существует равносильная формула, имеющая ПНФ.

Доказательство:

Алгоритм приведения к ПНФ.

1. Исключить эквиваленцию и импликацию (по законам 21 и 20).

2. Занести отрицание к атомарным формулам (по законам де Моргана 17 и 18).

3. Вынести кванторы вперед, используя (если нужно) переименование переменных (по законам 22, 23, 28 - 33).

Опр. Формула F имеет сколемовскую нормальную форму (СНФ), если 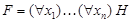, где H не содержит кванторов и имеет КНФ.

Теорема.

Для всякой формулы F существует формула, имеющая СНФ, одновременно с F выполнимая или невыполнимая. Доказательство:

Алгоритм приведения к СНФ.

1, 2, 3 - из алгоритма приведения к ПНФ.

Результат .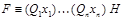

4. Бескванторную часть H привести к КНФ.

5. Исключить кванторы существования, поочередно слева направо, применяя одно из двух правил:

1 случай) 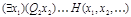~ 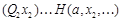, где a - символ константы.

2 случай) ~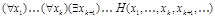

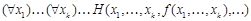~ , где 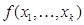- символ функции, зависящей от переменных .

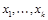При выполнении 1, 2, 3, 4 шагов алгоритма получается формула, равносильная F, следовательно, выполнимая или не выполнимая одновременно с F.

Если существует интерпретация j, при которой формула 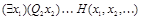истинна, то существует значение 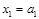, такое, что при этой же интерпретации j значение 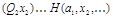истинно. Т.е. формула 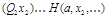выполнима.

Если существует интерпретация j, при которой формула 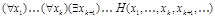истинна, то для любых значений переменных 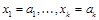существует подходящее значение 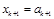, такое, что при этой же интерпретации j значение 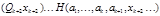истинно. Т.е. существует функция 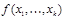( 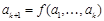), для которой формула 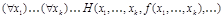выполнима.

Опр. Множество формул 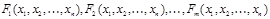выполнимо, если существует интерпретация 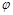на множестве M, и существуют элементы 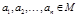, такие, что все значения 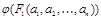, …, 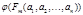истинны.

Невыполнимо - в противном случае.

Теорема.

Формула G является логическим следствием формул 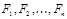Û множество формул 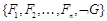не выполнимо.

10. Метод резолюций в логике предикатов

Опр. Подстановкой называется множество равенств 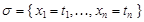, где 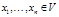, 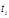- терм, не содержащий .

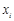Обозначение: 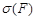- формула, полученная из F подстановкой s.

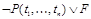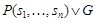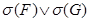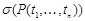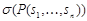Опр. Правило резолюций в логике предикатов - из дизъюнктов и выводится дизъюнкт , где подстановка s такая, что и совпадают.

«Наиболее общий унификатор».

Опр. Пусть S множество дизъюнктов. Будем говорить, что дизъюнкт 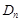выводится из S, если существует последовательность дизъюнктов 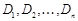, такая, что каждый 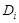принадлежит S,или получен по правилу резолюций из дизъюнктов 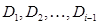, или получен подстановкой s.

Вывод 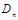из S - эта последовательность .

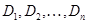Теорема.

Множество дизъюнктов S логики предикатов невыполнимо Û из S выводится пустой дизъюнкт.

Схема применения метода резолюций.

Дано: .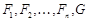

1. Формулы 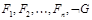привести к СНФ.

2. Отбросить кванторы общности.

3. Все получившиеся дизъюнкты собрать в множество S.

4. Построить вывод □ из S.

Языки и операции с ними

Опр. Алфавит S - конечное непустое множество.

Буква - каждый элемент множества S.

Слово над алфавитом S - конечная последовательность 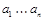, где каждая .

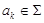(цепочка, string)

Длина слова 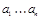- количество n символов в слове.

Пустое слово e - слово длины 0.

Обозначение 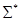- множество всех слов (включая пустое) над алфавитом S.

Опр. (Умножение слов)

Произведением слова 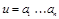на слово 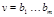называется слово .

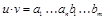(конкатенация)

Свойства:

1) умножение не коммутативно: ;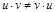

2) умножение ассоциативно: ;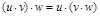

3) пустое слово e является нейтральным элементом относительно умножения: .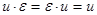

Следствие: 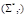- полугруппа с нейтральным элементом (моноид).

Опр. Степенью k слова u называется .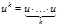

Опр. Языком над алфавитом S называется .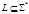

Пустым языком называется .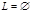

Пример.

1) Естественный (русский) язык.

2) Язык формул математической логики.

3) S ={0, 1}; язык компьютерных программ, записанных на автокоде.

Операции над языками:

пересечение 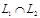; объединение ;

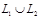дополнение 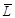(универсальным множеством является ).

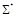Опр. Множество - набор каких-то объектов.

Элемент множества - каждый объект.

Множество содержит элемент: .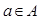

Опр. Пересечение множеств A и B - множество, состоящее из всех элементов, принадлежащих A и B одновременно.

A Ç B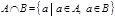

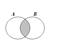
Опр. Объединение множеств A и B - множество, состоящее из всех элементов, принадлежащих или A, или B, или A и B одновременно (принадлежащих A или B).

A È B

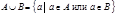
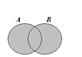
Опр. Универсальное множество для системы множеств - множество, содержащее все элементы этих множеств.

I

Опр. Дополнение к множеству A - множество, состоящее из всех элементов универсального множества, не принадлежащих A.

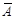
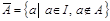
Опр. Произведением языков 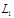и 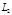называется язык

.

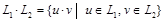Опр. Степенью k языка L называется

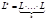
Обозначим .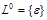

Опр. Итерацией языка L называется язык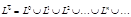

Приоритеты операций:

итерация	наивысший
умножение	высокий
дополнение	средний
пересечение, объединение	низший

Свойства операций:

1), 2) Идемпотентность

A Ç A = A;

A È A = A.

Замечание: ; .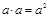

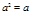3), 4) Коммутативность

A Ç B = B Ç A;

A È B = B È A.

5), 6) Ассоциативность

(A Ç B)Ç C= A Ç (B Ç C);

(A È B)È C= A È (B È C).

7), 8) Дистрибутивность

A Ç (B È C) = (A Ç B)È (A Ç C);

a × (b + c) = (a × b) + (a × c)

A È (B Ç C) = (A È B)Ç (A È C).

9), 10) Законы поглощения

A Ç (A È B) = A;

A È (A Ç B) = A.

11), 12)

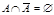закон противоречия;

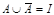закон «исключенного третьего».

13), 14) Законы де Моргана

;

.

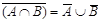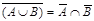19) Закон двойного отрицания

.

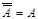20) ;

;

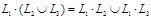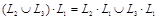21) ; ;

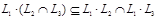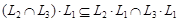22) ;

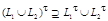23) .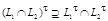