Размещения, перестановки, сочетания
АУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА №1
Элементы комбинаторики
Некоторые формулы и задачи комбинаторного анализа (комбинаторики) представлены в данной книге в связи с тем, что они используются во многих задачах классической теории вероятностей.
Принцип умножения и принцип сложения
Принцип умножения
Пусть требуется выполнить 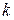 упорядоченных и взаимоисключающих друг друга действий. Если первое из этих действий можно выполнить
упорядоченных и взаимоисключающих друг друга действий. Если первое из этих действий можно выполнить 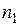 способами, второе —
способами, второе — 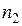 способами, …,
способами, …, 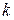 – е действие —
– е действие — 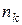 способами, то все
способами, то все 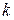 упорядоченных действий можно выполнить
упорядоченных действий можно выполнить 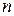 способами, где
способами, где
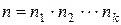 . (1.1)
. (1.1)
Задача 1.1. Сколько существует всевозможных шестизначных чисел?
Решение: Первая цифра числа не может быть нулем. Следовательно, первой может быть любая из цифр от 1 до 9. Остальные пять мест в числе могут быть заняты любой из десяти цифр. Поэтому согласно принципу умножения, количество шестизначных чисел равно:
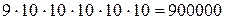
Принцип сложения
Если для выполнения какого–то действия имеется: 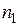 , или
, или 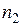 , …., или
, …., или 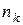 взаимно исключающих друг друга способов, то общее количество способов, которое можно использовать для выполнения этого действия, равно:
взаимно исключающих друг друга способов, то общее количество способов, которое можно использовать для выполнения этого действия, равно:
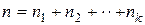 . (1.2)
. (1.2)
Задача 1.2. Сколько пар разных пирожных можно выбрать, если имеется десять пирожных "Эклер", семь пирожных "Буше" и восемь корзиночек?
Решение: Пары пирожных могут составляться из пирожных "Эклер" и "Буше", для этого имеется 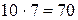 вариантов. Пары пирожных могут быть составлены из пирожных "Эклер" и корзиночек — таких
вариантов. Пары пирожных могут быть составлены из пирожных "Эклер" и корзиночек — таких 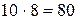 вариантов. И, наконец, это могут быть пирожные "Буше" и корзиночки —
вариантов. И, наконец, это могут быть пирожные "Буше" и корзиночки — 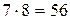 вариантов. Общее количество способов
вариантов. Общее количество способов 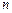 определяется по принципу сложения (1.2)
определяется по принципу сложения (1.2)
Размещения, перестановки, сочетания
Пусть имеется множество 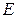 , содержащее
, содержащее 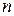 элементов, и из этого множества делаются выборки по
элементов, и из этого множества делаются выборки по 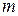 элементов в каждой
элементов в каждой 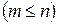 .
.
Размещениями называются упорядоченные выборки из множества 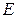 . Число размещений из
. Число размещений из 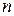 элементов по
элементов по 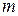 вычисляется по формуле:
вычисляется по формуле:
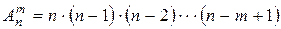 , (1.3)
, (1.3)
или
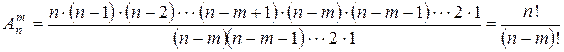 .
.
замечание 1
В среде Mathcad число размещений из 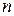 по
по 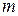
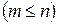 можно вычислять с помощью встроенной функции permut (n, m).
можно вычислять с помощью встроенной функции permut (n, m).
Задача 1.3. Имеется множество 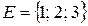 . Из элементов этого множества составляются двухэлементные упорядоченные множества:
. Из элементов этого множества составляются двухэлементные упорядоченные множества:
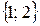 ,
, 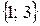 ,
, 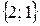 ,
, 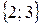 ,
, 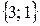 ,
, 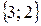 .
.
Чтобы убедиться, что мы выписали все размещения, определим их количество, используя формулу (1.3):
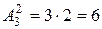 .
.
При 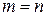 размещения называются перестановками. Число перестановок из
размещения называются перестановками. Число перестановок из 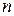 элементов равно
элементов равно
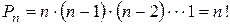 . (1.4)
. (1.4)
замечание 2
В среде Mathcad число перестановок из 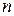 можно вычислять по формуле (1.4), набирая с клавиатуры
можно вычислять по формуле (1.4), набирая с клавиатуры 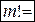 или с помощью встроенной функции permut (n, n).
или с помощью встроенной функции permut (n, n).
Задача 1.4
Сколько шестизначных чисел с различными цифрами можно составить из цифр 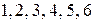 ?
?
Решение: Количество таких чисел равно числу размещений из шести по шесть, т.е. числу перестановок из шести. Поэтому
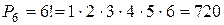 .
.
Сочетаниями называются неупорядоченные выборки из множества 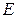 . Число сочетаний из
. Число сочетаний из 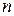 элементов по
элементов по 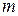 вычисляется по формуле
вычисляется по формуле
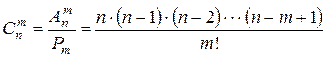 . (1.4)
. (1.4)
замечание 3
В среде Mathcad число сочетаний из 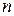 по
по 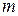
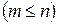 можно вычислять по формуле с помощью встроенной функции combin (n, m).
можно вычислять по формуле с помощью встроенной функции combin (n, m).
Задача 1.5
Если в задаче 1.3 из элементов этого множества 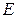 составляются двухэлементные неупорядоченные множества, то число таких множеств — число сочетаний из трех элементов по два – равно 3, т.к. одинаковыми сочетаниями будут множества
составляются двухэлементные неупорядоченные множества, то число таких множеств — число сочетаний из трех элементов по два – равно 3, т.к. одинаковыми сочетаниями будут множества 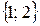 и
и 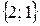 ,
, 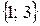 и
и 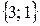 ,
, 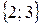 и
и 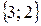 . Поэтому сочетаниями будут только следующие три выборки:
. Поэтому сочетаниями будут только следующие три выборки:
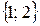 ,
, 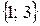 ,
, 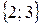 .
.
Для сочетаний часто более удобной является формула:
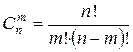 . (1.5)
. (1.5)
Например, 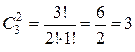 .
.
замечание 4
При вычислении числа сочетаний следует учитывать, что:
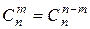 ,
, 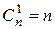 ,
, 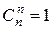 .
.
Задача 1.6. Сколько четырехзначных чисел можно составить, используя для их записи только две цифры?
Решение: Если числа составляются из цифр 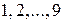 , то имеется
, то имеется 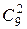 вариантов выбора двух цифр из девяти. Каждая позиция четырехзначного числа может быть заполнена одной из двух выбранных цифр, т.е. имеется
вариантов выбора двух цифр из девяти. Каждая позиция четырехзначного числа может быть заполнена одной из двух выбранных цифр, т.е. имеется 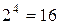 вариантов составления числа. При этом должны быть исключены два случая, при которых четырехзначное число состоит из одинаковых цифр. Поэтому, согласно принципу умножения (1.1), количество
вариантов составления числа. При этом должны быть исключены два случая, при которых четырехзначное число состоит из одинаковых цифр. Поэтому, согласно принципу умножения (1.1), количество 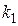 четырехзначных чисел, составленных из цифр
четырехзначных чисел, составленных из цифр 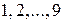 равно:
равно:
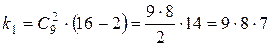

Рис. 1
Иначе следует подсчитывать количество четырехзначных чисел, в записи которых есть ноль, поскольку число не может начинаться с нуля. Первая позиция таких чисел может быть занята одной их цифр 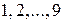 , т.е. имеется 9 вариантов выбора. Остальные три позиции могут быть заняты этой же цифрой или нулем, за исключением случая, когда в записи числа одна цифра, т.е.
, т.е. имеется 9 вариантов выбора. Остальные три позиции могут быть заняты этой же цифрой или нулем, за исключением случая, когда в записи числа одна цифра, т.е. 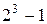 вариантов выбора. Поэтому количество
вариантов выбора. Поэтому количество 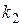 таких чисел равно
таких чисел равно
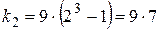 .
.
Искомое количество четырехзначных чисел определяется по принципу сложения (1.2):
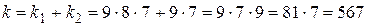 .
.
На рис. 1 показаны расчеты в среде Mathcad для задач 1.3 —1.6.
Задача 1.7. В группе из 30 студентов 20 знают английский язык. Сколькими способами можно выбрать из этой группы трех студентов, чтобы хотя бы один из них знал английский язык?
Решение этой задачи в среде Mathcad показано на рис. 1.
