Совокупный коэффициент детерминации

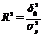, или

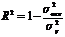
где 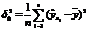– факторная дисперсия теоретических значений результативного признака, отражает влияние на вариацию у всех включенных в модель факторов;

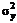– общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;

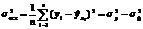– остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.

При линейной форме связи расчет совокупного коэффициента детерминации можно выполнить по формуле:

,

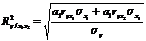Совокупный коэффициент множественной корреляции R
представляет собой квадратный корень из совокупного множественного
коэффициента детерминации R². Коэффициент множественной корреляции изменяется в пределах от 0 до 1 и по определению положителен: .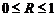

В случае зависимости результативного признака от двух факторов множественный коэффициент корреляции R может быть вычислен по формуле:

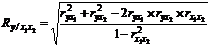, (35)

где 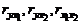– парные коэффициенты корреляции между признаками.

Отсюда вытекает условие включения факторов в модель:

Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками.

Частный коэффициент детерминации:

,

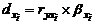где 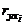– парный коэффициент корреляции между результативным и i-м факторным признаком;

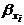– соответствующий стандартизованный коэффициент уравнения множественной регрессии:

.

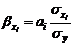Частные коэффициенты корреляциидля 2-х факторной модели:

; .

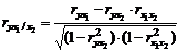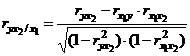В первом случае исключено влияние факторного признака х₂, во втором – х₁

Для оценки сравнительной силы влияния факторов,
по каждому фактору рассчитывают частные коэффициенты
эластичности:

,

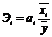где 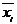– среднее значение соответствующего факторного признака;

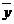– среднее значение результативного признака;

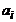– коэффициент регрессии при i-м факторном признаке.

Сумма частных коэффициентов эластичности 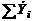позволяет оценить эластичность в целом при совокупном изменении всех факторов.

Оценка связи на основе теоретического
корреляционного отношения (шкала Чеддока)

Значение	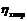Характер связи	Значение	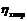Характер связи
η = 0	Отсутствует	0,5 ≤ η < 0,7	Заметная
0 < η < 0,2	Очень слабая	0,7 ≤ η < 0,9	Сильная
0,2 ≤ η < 0,3	Слабая	0,9 ≤ η < 1	Весьма сильная
0,3 ≤ η < 0,5	Умеренная	η = 1	Функциональная

Для парной линейной зависимости теоретическое корреляционное отношение равно линейному коэффициенту корреляции (η = |r|). Аналогично для множественной линейной зависимости – η = R.

14. Понятие динамики. Виды рядов динамики.

Статистика рассматривает общественные явления в непрерывном развитии.

Ряд динамики – последовательно расположенные в хронологическом порядке показатели, характеризующие общественные явления и процессы в развитии. В ряду динамики для каждого отрезка времени приводится два показателя:

- показатель времени

- показатель уровня ряда (у).

Кроме них могут также показываться производные.

Исследование рядов динамики дает возможность показать развитие явления во времени, тенденции развития, темпы роста, основные пути развития. Ряды динамики могут состоять из

- абсолютных;

- относительных;

- средних величин.

Примером ряда динамики средних величин является урожайность культур по хозяйствам области; ср. производительности.

Примером ряда динамики относительных величин может быть ряд, характеризующий темпы роста производства продукции.

Ряд динамики абсолютных величин характеризует уровни развития общественных явлений, либо на определенные моменты времени, либо за определенные промежутки времени. В зависимости от этого ряды динамики делят на:

- интервальные;

- моментные.

Разница между ними заключается в том, что в моментном ряду интервал – это промежуток времени между датами, а в интервальном – это промежуток времени, за который обобщены приводимые сведения.

На основе ряда динамики абсолютных величин могут быть получены ряды динамики относительных и средних величин.

Полный ряд динамики - ряд, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке.

Неполный ряд динамики - это ряд, в котором уровни зафиксированы в неравностоящие моменты.

Основные случаи несопоставимости рядов динамики:

1) территориальные изменения объекта исследования, к которому относится изучаемый показатель;

2) разновеликие интервалы времени, к которым относится показатель;

3) изменение даты учета;

4) изменение методологии учета или расчета показателя;

5) изменение цен;

6) изменение единиц измерения.

На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.

Периодизации динамики - процесс выделения однородных этапов развития.

Характеристика рядов динамики в зависимости от расстояния между уровнями:

1) с равностоящими уровнями;

2) с неравностоящими уровнями во времени.

Равностоящие ряды динамики - ряды динамики одинаковых периодов, или следующих через равные промежутки времени показателей.

Неравностоящие ряды динамики - ряды с неровными периодами или неравномерными промежутками между датами.

Основное условие правильного построения ряда динамики - сопоставимость всех входящих в него уровней.

Смыкание рядов динамики - объединение в одни ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам.

Условия смыкания рядов; необходимо, чтобы по одному из периодов (переходному) имелись данные, исчисленные по разной методологии (или в разных границах).

15. Характеристика уровней развития изучаемых явлений во времени: определение абсолютных относительных и обобщающих показателей динамики.

При изучении явления во времени исследуется интенсивность изменения и производится расчет средних показателей динамики.

Анализ интенсивности изменения во времени осуществляет­ся с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процен­та прироста.

Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.

Показатели анализа динамики могут вычисляться на посто­янной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, –базисным.

Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же ба­зисным уровнем. В качестве базисного выбирается либо началь­ный уровень в ряду динамики, либо уровень, с которого начи­нается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.

Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с преды­дущим. Вычисленные таким образом показатели анализа дина­мики называются цепными.

Важнейшим статистическим показателем анализа динамики яв­ляется абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за оп­ределенный промежуток времени. Абсолютный прирост с пере­менной базой называют скоростью роста.

Абсолютный прирост (цепной)

;

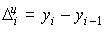абсолютный прирост (базисный)

,

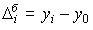где 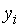– уровень сравниваемого периода; 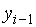– уровень предшествующего периода; 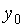– уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток вре­мени

.

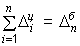Абсолютное изменение уровня не является константой тенденции. Оно со временем изменяется, т.е. уровни ряда изменяются с ускорением.

Ускорение – это разность между абсолютным изменением за данный период и абсолютным изменением за предыдущий период равной длительности

.

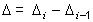Показатель абсолютного ускорения применяется только в цепном варианте. Отрицательная величина ускорения говорит о замедлении роста.

Для оценки интенсивности используются относительные показатели динамики, т.е. показатели относительного изменения уровня динамического ряда за какой-либо период времени.

Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называетсякоэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения.

Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.

Коэффициент роста (цепной) = ;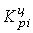

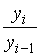коэффициент роста (базисный) = ;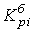

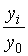темп роста (цепной) = ;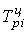

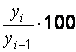темп роста (базисный) = .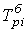

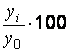Между цепными и базисными коэффициентами роста суще­ствует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведе­ние последовательных цепных коэффициентов роста равно базис­ному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста

.

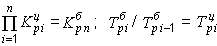Относительную оценку скорости измерения уровня ряда в еди­ницу времени дают показатели темпа прироста (сокращения).

Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного при­роста к абсолютному уровню, принятому за базу сравнения.

Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста).

Темп прироста (цепной) = ;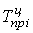

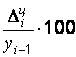темп прироста (базисный) = .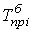

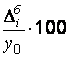Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%; коэффициент прироста получается вычитанием единицы из коэффициента роста:

(для цепных и базисных) 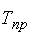= 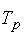- 100; 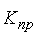= 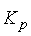- 1.

При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедле­нии) темпов прироста абсолютный прирост не всегда уменьша­ется, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:

; .

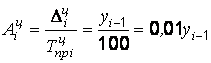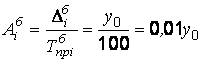Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным пока­зателем — одним процентом прироста.

В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста (прироста) двух смежных периодов

; = – ; = .

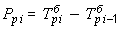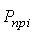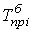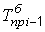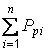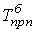В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в ре­зультате получаем темп прироста соответствующего периода по сравнению с базисным.

Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средниеуровни ряда и средние показатели изменения уровней ряда.

Средний уровень ряда характеризует обобщённую вели­чину абсолютных уровней.

Методы расчета среднего уровня интервального и моментного рядов динамики различны.

Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической:

при равных интервалах применяется средняя арифметиче­ская простая

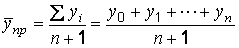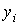( – абсолютные уровни ряда; 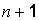– число уровней ряда);

при неравных интервалах – средняя арифметическая взве­шенная

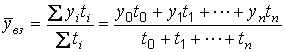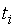( – веса, длительность интервалов времени (дней, ме­сяцев) между смежными датами; 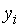– уровни ряда динамики, сохраняющиеся без изме­нения в течение промежутка времени ).

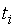Средний уровень моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической моментного ряда

;

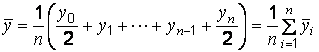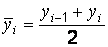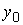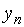( ,…, – уровни периода, за который делается расчет; 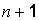– число уровней).

Средний уровень моментных рядов с неравностоящими уровнями определяется по формуле средней хронологической взвешенной

= ,

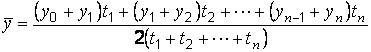где 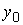,…, 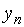– уровни рядов динамики, 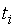– интервал времени между смежными уровнями.

Обобщающий показатель скорости изменения уровней во времени – средний абсолютный прирост(убыль), представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как среднюю арифметическую простую

,

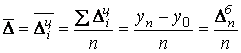где 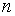– число цепных абсолютных приростов 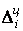в изучаемом периоде.

Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за едини­цу времени изменяется уровень ряда динамики.

Средний темп роста (снижения) – обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (сни­жения) применяется определяющий показатель – произведение цепных темпов роста, равное темпу роста за весь рассматривае­мый период.

Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах ( 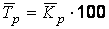), то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):

= ,

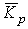где 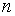– число цепных коэффициентов роста 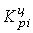; 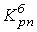– базисный коэффициент роста за весь период.

Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода 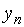на уровень базисного периода .

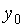Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):

= .

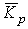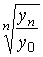Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:

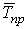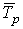= - 100 ; 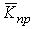= 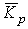- 1 ,

где 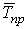– средний темп прироста; 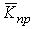– средний коэффициент прироста.

16. Понятие тренда и методы его выявления.

В ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления (тренда) и сглаживание случайных колебаний. Для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания.

Выделяют три основных способа обработки динамического ряда:

а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала;

б) метод скользящей средней;

в) аналитическое выравнивание (выравнивание по аналитическим формулам).

Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.

По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.

Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:

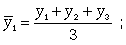
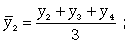
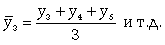(9.19)

При четных периодах скользящей средней можно центрировать данные, т.е. определять среднюю из найденных средних. К примеру, если скользящая исчисляется с продолжительностью периода, равной 2, то центрированные средние можно определить так:

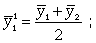
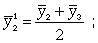
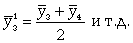(9.20)

Первую рассчитанную центрированную относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m - 1)/2, где m - число уровней интервала.

Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.

Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:

1) используя полусумму уровней, расположенных рядом с интерполируемыми;

2) по среднему абсолютному приросту;

3) по темпу роста.

Способ определения количественных значений за пределами ряда называют экстраполяцией. Экстраполирование используется для прогнозирования тех факторов, которые не только в прошлом и настоящем обусловливают развитие явления, но и могут оказать влияние на его развитие в будущем.

Экстраполировать можно по средней арифметической, по среднему абсолютному приросту, по среднему темпу роста.

При аналитическом выравнивании может иметь место автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле

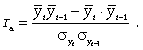(9.21)

Автокорреляцию в рядах можно устранить, коррелируя не сами уровни, а так называемые остаточные величины (разность эмпирических и теоретических уровней). В этом случае корреляцию между остаточными величинами можно определить по формуле

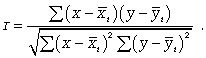(9.22)

При изучении динамики любого из явлений, главной задачей анализа ставится выявление основной тенденции в развитии. Количественная характеристика явления в динамике многих факторов и их развитии зависит от этих факторов.

Для этого используют сглаживание рядов динамики по методу скользящей средней или по методу аналитического выравнивания уровней ряда динамики.

Для того, чтобы сгладить ряд по 5 дням необходимо по каждым последующим 5 дням рассчитать среднюю арифметическую простую, при этом среднее число за первых 5 дней поставить на 3-ю дату, а следующие 5 дней начинать рассчитывать со 2-го числа, а результат ставить на 4-ю дату. Чем больше интервал, за который исчисляется средняя, тем больше сглаженный ряд усредняет фактический ряд, при этом теряется много информации. Чем меньше интервал, тем больше сглаженный ряд приближается к конкретному ряду. По сглаженному ряду, показанному на графике можно выявить тенденцию в развитии.